Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
A derived distribution useful in actuarial science
ResourceFunction["TimeShiftedDistribution"][xmin,dist] represents a distribution dist that has been truncated to lie above xmin and then translated so that the lowest outcome is 0. | |
ResourceFunction["TimeShiftedDistribution"][{xmin,ymin,…},dist] represents a multivariate truncation of the distribution dist, translated so the lowest outcome from the distribution is a vector of 0s. |
A BinomialDistribution, time-shifted so that its value must lie above 3 and be translated to the left by 3:
| In[1]:= |
| Out[1]= |
The probability density (mass) function of that distribution:
| In[2]:= |
| Out[3]= | 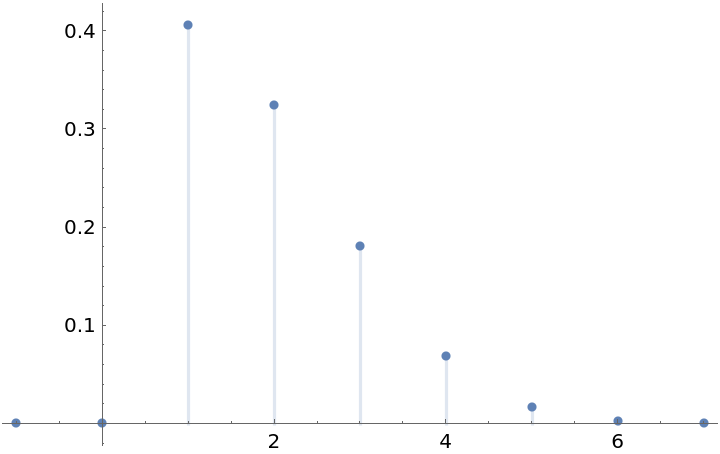 |
The distribution of the remaining life of a person aged 61, where longevity at birth is distributed according to a GompertzMakehamDistribution:
| In[4]:= |
| Out[4]= |
The survival function of that time-shifted distribution:
| In[5]:= |
| Out[5]= | 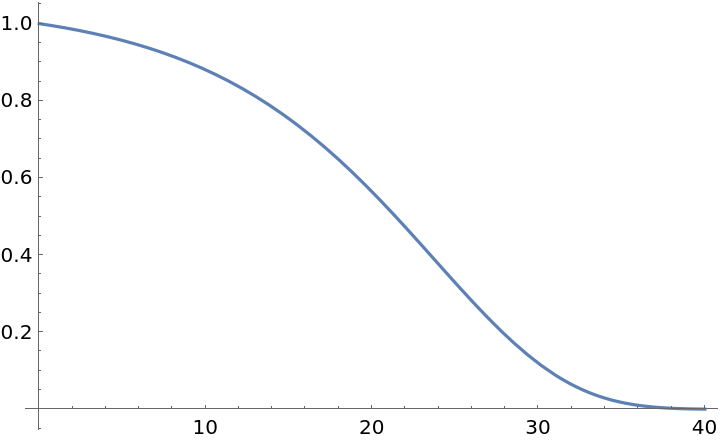 |
The mean of a time-shifted distribution of a ProductDistribution of two symbolic BetaDistributions:
| In[6]:= | ![TraditionalForm@
Refine[Mean@
ResourceFunction["TimeShiftedDistribution"][{x, y}, ProductDistribution[BetaDistribution[a1, b1], BetaDistribution[a2, b2]]], {0 < x < 1, 0 < y < 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/3d5/3d5d5c2f-5efc-477a-9523-61c818299066/3ee2cdf71d099ac8.png) |
| Out[6]= | 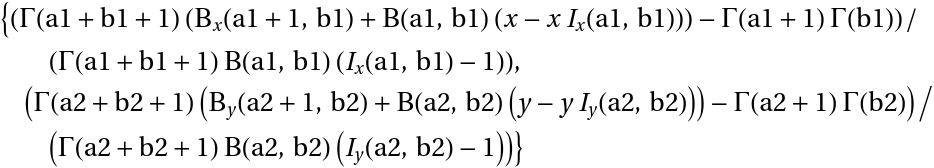 |
A random variable drawn from a time-shifted MultinormalDistribution:
| In[7]:= |
| Out[7]= |
The numeric probability of a draw from a time-shifted CopulaDistribution falling into a particular set of values:
| In[8]:= | ![NProbability[
0 < x < 2 && y > 0.3, {x, y} \[Distributed] ResourceFunction["TimeShiftedDistribution"][{2, 2}, CopulaDistribution[{"Binormal", -0.3}, {NormalDistribution[0, 1], NormalDistribution[0.5, 0.7]}]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/3d5/3d5d5c2f-5efc-477a-9523-61c818299066/0e6ec010ddfde87d.png) |
| Out[8]= |
Show survival functions of a BetaDistribution for different time-shift values:
| In[9]:= | ![With[{survivalFunctions = Table[SurvivalFunction[
ResourceFunction["TimeShiftedDistribution"][t, BetaDistribution[3, 3]], x], {t, Range[0, 0.8, 0.1]}]}, Plot[survivalFunctions, {x, 0, 1},
PlotLabel -> "Time Shifted Survival Functions\nof a Beta Distribution", PlotLegends -> Placed[LineLegend[Range[0, 0.8, 0.1], LegendLabel -> "Time Shift"],
Bottom]]]](https://www.wolframcloud.com/obj/resourcesystem/images/3d5/3d5d5c2f-5efc-477a-9523-61c818299066/5a63e11407ffb532.png) |
| Out[9]= | 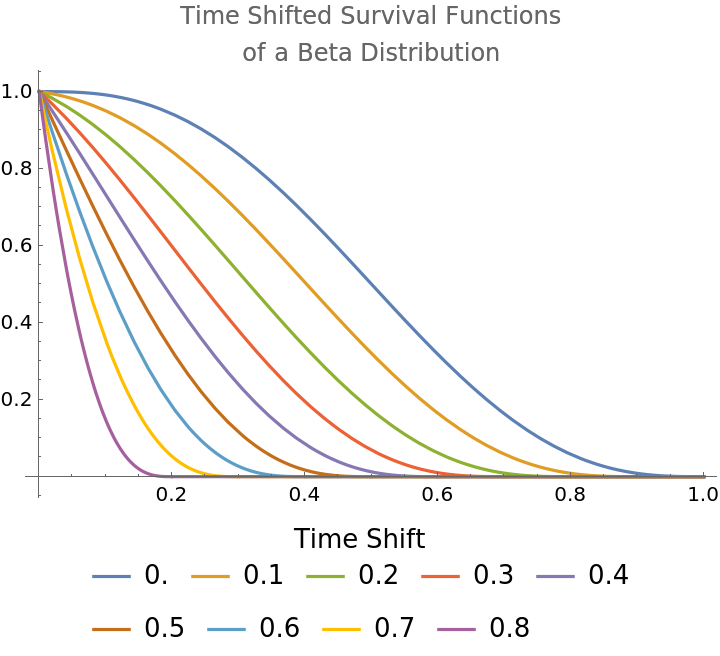 |
Show survival functions of a GompertzMakehamDistribution for different time-shift values:
| In[10]:= | ![With[{survivalFunctions = Table[SurvivalFunction[
ResourceFunction["TimeShiftedDistribution"][t, GompertzMakehamDistribution[1/8, 1/40000]], x], {t, Range[0, 90, 10]}]}, Plot[survivalFunctions, {x, 0, 100},
PlotLabel -> "Time Shifted Survival Functions\nof a Gompertz-Makeham Distribution", PlotLegends -> Placed[LineLegend[Range[0, 90, 10], LegendLabel -> "Time Shift"], Bottom]]]](https://www.wolframcloud.com/obj/resourcesystem/images/3d5/3d5d5c2f-5efc-477a-9523-61c818299066/34f99d207b462943.png) |
| Out[10]= |  |
Some distributions, such as the ExponentialDistribution, remain unchanged after time shifting :
| In[11]:= |
| Out[11]= |
Consider a life insurance product in which the time a person dies and the time a person lets their policy lapse are given by the ProductDistribution of a GompertzMakehamDistribution (for longevity) and an ExponentialDistribution (for lapse). The insured has neither died nor lapsed before age 61. Compute the probability that an insurer will have to pay a death benefit between k and k+1 years thereafter and that the insurance policy will not have lapsed by that time:
| In[12]:= |
| In[13]:= |
| Out[13]= |  |
| In[14]:= |
| Out[14]= | 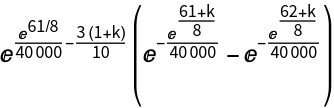 |
Compute the actuarial present value of a death benefit of $1 for such a person, assuming the policy pays nothing if the policy lapses before death and assuming a 5% effective rate of interest:
| In[15]:= |
| Out[15]= |
Compute the maximum amount the insurer would be willing to pay a 75-year-old who holds such a policy to let it lapse, again assuming a 5% effective rate of interest:
| In[16]:= | ![NExpectation[
If[death < lapse, 1/(1 + 0.05)^death, 0], {death, lapse} \[Distributed] ResourceFunction["TimeShiftedDistribution"][{75, 75}, ProductDistribution[GompertzMakehamDistribution[1/8, 1/40000], ExponentialDistribution[3/10]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/3d5/3d5d5c2f-5efc-477a-9523-61c818299066/45e03c106b161eb7.png) |
| Out[16]= |
This work is licensed under a Creative Commons Attribution 4.0 International License