Basic Examples (4)
Tetration of 2 with order 3:
Symbolic tetration:
Infinite tetration of a real number:
Infinite tetration of ⅈ:
Scope (3)
Compute infinite tetrations of real numbers inside the convergence interval:
Compute tetrations of real numbers within the divergence interval 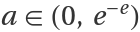 :
:
Compute tetrations of real numbers within the divergence interval 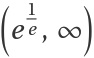 :
:
Properties and Relations (5)
Behavior of the tetration of real numbers inside the divergence interval 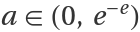 :
:
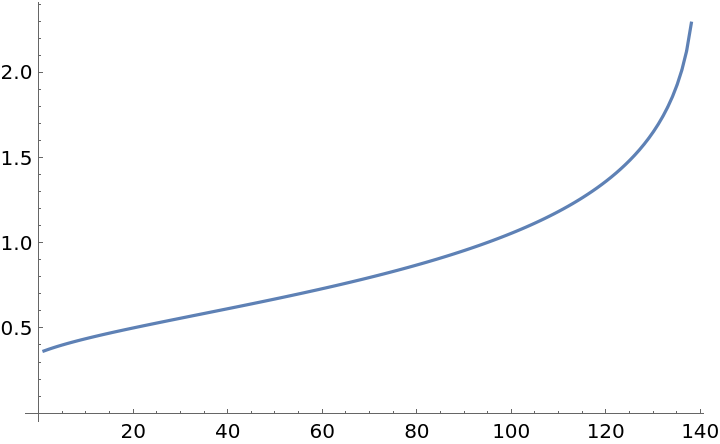
Behavior of infinite tetration of real numbers inside the convergence interval 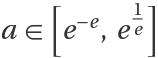 :
:
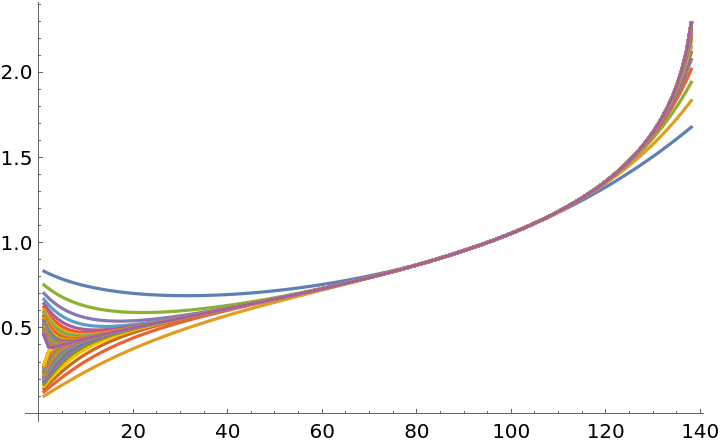
Evolution and stabilization of the tetration curve inside the convergence interval for increasing k in a single plot:
Tetration convergence curve:
Behavior of the tetration of real numbers within the divergence interval 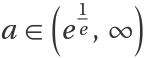 :
:
The highly divergent property of tetration is easy to see from the previous plots.
Neat Examples (5)
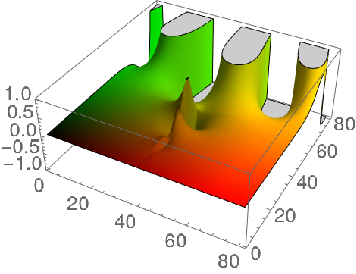
Real part plot of tetration order 3 for a range of complex values:
Imaginary part plot of tetration order 2:
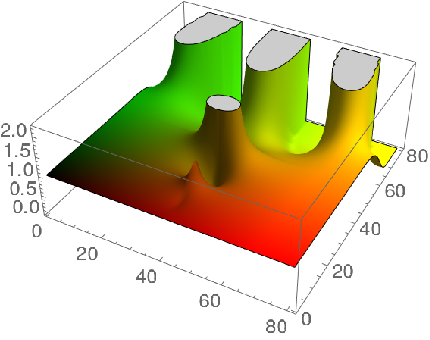
Norm plot of tetration order 3:
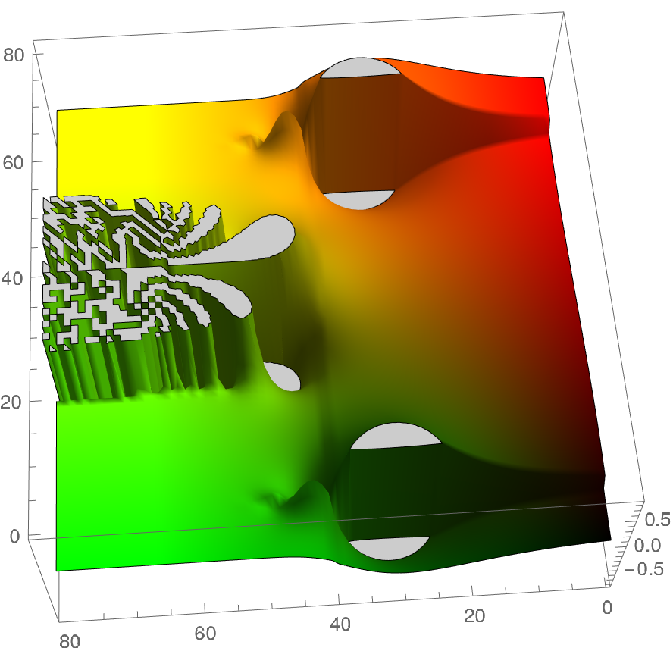
Imaginary part of tetration order 2 of a number ez, where z is a complex number:
Real part of tetration order 2 of a number ez, where z is a complex number:
Possible Issues (3)
Tetration of a=0 is Indeterminate:
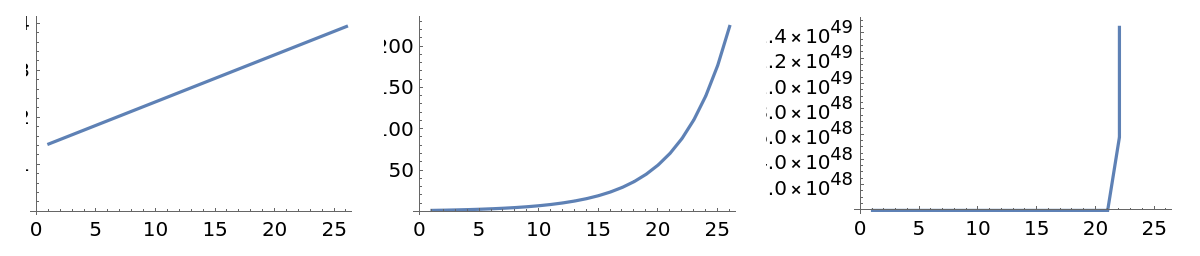
Computing tetration for large values of k within the divergence interval 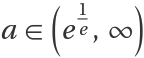 may cause overflow, because the tetration exceeded the maximum machine number. You can obtain the maximum k for a given a as such:
may cause overflow, because the tetration exceeded the maximum machine number. You can obtain the maximum k for a given a as such:
Maximum tetration for a=12:
If you want to avoid long execution times, use the function N to get an approximated result:
Large values of k cause an overflow:
Infinite tetration does not exists outside the convergence interval:
![]() :
:![]() :
:
![]() :
:![GraphicsRow[
Table[ListLinePlot[
Table[ResourceFunction["Tetration"][x, n], {x, 0 + 0.0001, (1/E)^(E) - 0.0001, 0.0001}]], {n, {101, 200, 301, 400}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/58f/58ffdf33-4d63-4195-8e83-c2bc5e515771/1b644ebfe1ebd72b.png)

![]() :
:![GraphicsRow[
Table[ListLinePlot[
Table[ResourceFunction["Tetration"][x, n], {x, E^(\[Minus]E), E^(1/E), 0.01}]], {n, {2, 3, 4, 100, 1000, 10000}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/58f/58ffdf33-4d63-4195-8e83-c2bc5e515771/730b2aa827d2ba76.png)

![]() :
:
![ListPlot3D[
Table[Re[ResourceFunction["Tetration"][x + I*y, 3]], {x, xrange}, {y,
yrange}] , ColorFunction -> Function[{x, y, z}, RGBColor[x, y, 0.]], Mesh -> None]](https://www.wolframcloud.com/obj/resourcesystem/images/58f/58ffdf33-4d63-4195-8e83-c2bc5e515771/3598a33397828656.png)

![ListPlot3D[
Table[Im[ResourceFunction["Tetration"][x + I*y, 2]], {x, xrange}, {y,
yrange}] , ColorFunction -> Function[{x, y, z}, RGBColor[x, y, 0.]], Mesh -> None]](https://www.wolframcloud.com/obj/resourcesystem/images/58f/58ffdf33-4d63-4195-8e83-c2bc5e515771/03e31d191191b5de.png)
![ListPlot3D[
Table[Norm[ResourceFunction["Tetration"][x + I*y, 3]], {x, xrange}, {y, yrange}] , ColorFunction -> Function[{x, y, z}, RGBColor[x, y, 0.]], Mesh -> None]](https://www.wolframcloud.com/obj/resourcesystem/images/58f/58ffdf33-4d63-4195-8e83-c2bc5e515771/527c73249492dc03.png)
![ListPlot3D[
Table[Im[ResourceFunction["Tetration"][Exp[x + I*y], 2]], {x, xrange}, {y, yrange}] , ColorFunction -> Function[{x, y, z}, RGBColor[x, y, 0.]], Mesh -> None]](https://www.wolframcloud.com/obj/resourcesystem/images/58f/58ffdf33-4d63-4195-8e83-c2bc5e515771/3724059b61fd4b3e.png)
![ListPlot3D[
Table[Re[ResourceFunction["Tetration"][Exp[x + I*y], 2]], {x, xrange}, {y, yrange}] , ColorFunction -> Function[{x, y, z}, RGBColor[x, y, 0.]], Mesh -> None]](https://www.wolframcloud.com/obj/resourcesystem/images/58f/58ffdf33-4d63-4195-8e83-c2bc5e515771/25f9d1067ad8efd6.png)
![]() may cause overflow, because the tetration exceeded the maximum machine number. You can obtain the maximum k for a given a as such:
may cause overflow, because the tetration exceeded the maximum machine number. You can obtain the maximum k for a given a as such:![MaxTetrationK[a_] := Module[{k, y},
k = 0; (**init k**)
y = 1; (**init tetration**) Quiet[While[y != Overflow[],
k = k + 1;
y = ResourceFunction["Tetration"][N[a], k] ;
]];
Return[k - 1]
]](https://www.wolframcloud.com/obj/resourcesystem/images/58f/58ffdf33-4d63-4195-8e83-c2bc5e515771/2d8cc285f8a7017e.png)