Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 TetrahelixMesh

Source Notebook

Generate a mesh region representing the tetrahelix

Contributed by: Jan Mangaldan

ResourceFunction["TetrahelixMesh"][n,s]

gives a mesh region representing the Boerdijk–Coxeter tetrahelix made from n regular tetrahedra of unit edge length, with s set to 1 for the counterclockwise orientation or -1 for the clockwise orientation.

ResourceFunction["TetrahelixMesh"][n]

gives a mesh region representing an counterclockwise tetrahelix.

Details

ResourceFunction["TetrahelixMesh"] is also known as the Boerdijk–Coxeter helix.
The tetrahelix is a linear stacking of regular tetrahedra, arranged so that the edges of the complex that belong to only one tetrahedron form three intertwined helices.
ResourceFunction["TetrahelixMesh"] takes the same options as MeshRegion.

Examples

Basic Examples (2) 

A tetrahelix with 10 tetrahedra, oriented counterclockwise:

In[1]:=
ResourceFunction["TetrahelixMesh"][10]
Out[1]=

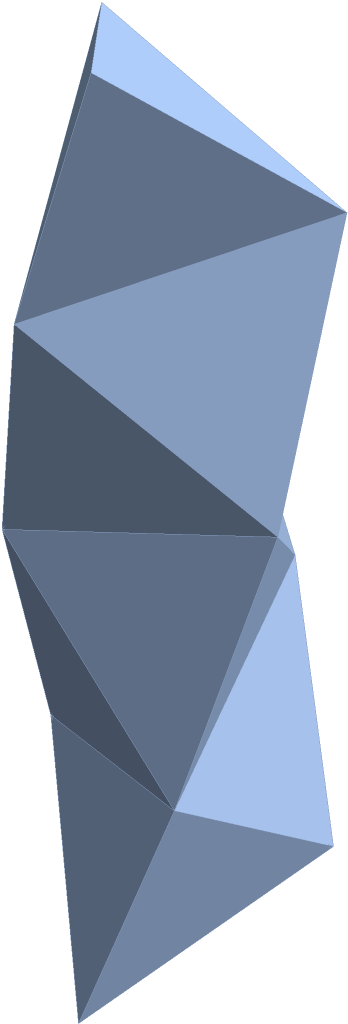
A tetrahelix with 10 tetrahedra, oriented clockwise:

In[2]:=
ResourceFunction["TetrahelixMesh"][10, -1]
Out[2]=

Scope (2) 

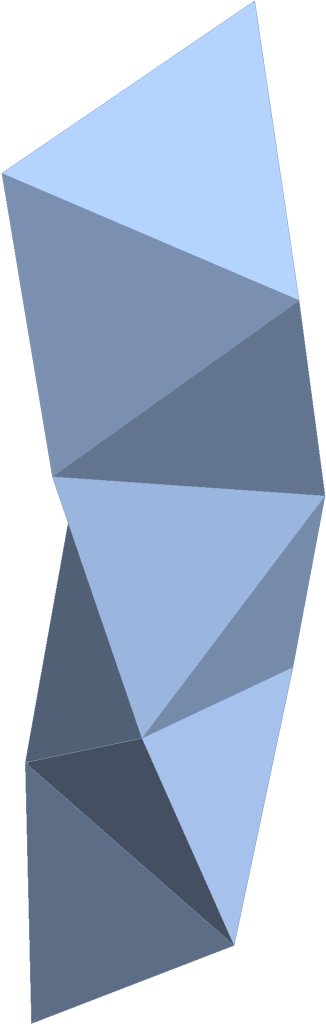
Use MeshRegion options to change the style:

In[3]:=
ResourceFunction["TetrahelixMesh"][4, MeshCellStyle -> {1 -> Directive[Thick, Blue], 2 -> Opacity[0.6, Red]}]
Out[3]=

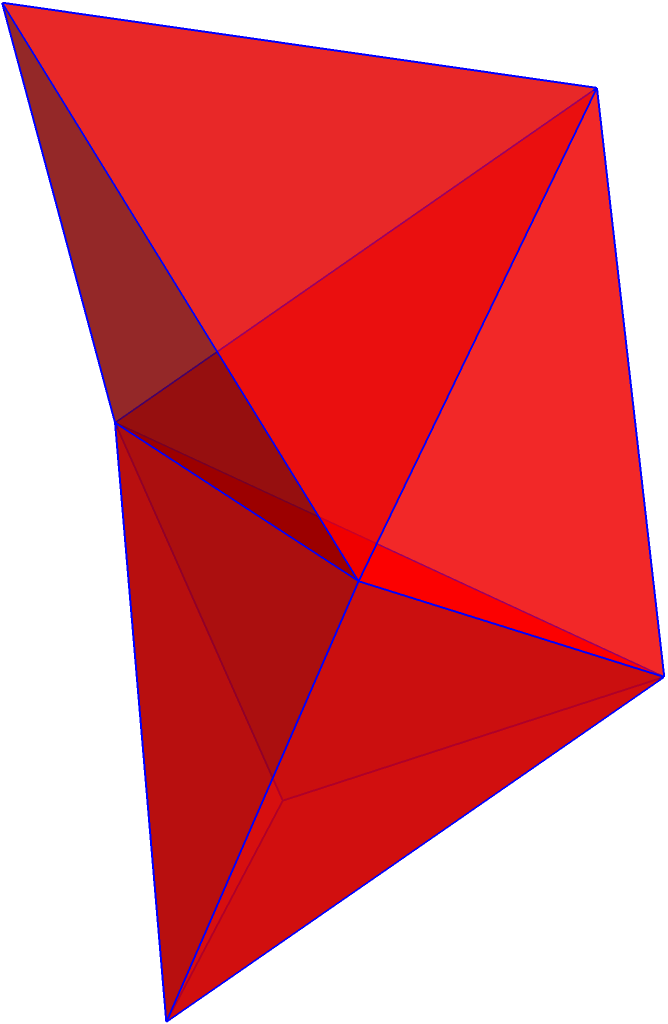
Compute the volume and surface area of the helix:

In[4]:=
With[{bcm = ResourceFunction["TetrahelixMesh"][10]}, {Volume[bcm], SurfaceArea[bcm]}]
Out[4]=

These can be expressed in terms of the volume and surface area of a single tetrahedron:

In[5]:=
With[{n = 10}, {n PolyhedronData["Tetrahedron", "Volume"], (n + 1)/ 2 PolyhedronData["Tetrahedron", "SurfaceArea"]}] // N
Out[5]=

Properties and Relations (3) 

Use TransformedRegion to rescale or translate the tetrahelix:

In[6]:=
TransformedRegion[ResourceFunction["TetrahelixMesh"][7], TranslationTransform[{1, -1, 1}]@*ScalingTransform[{3/2, 3/2, 3/2}]]
Out[6]=

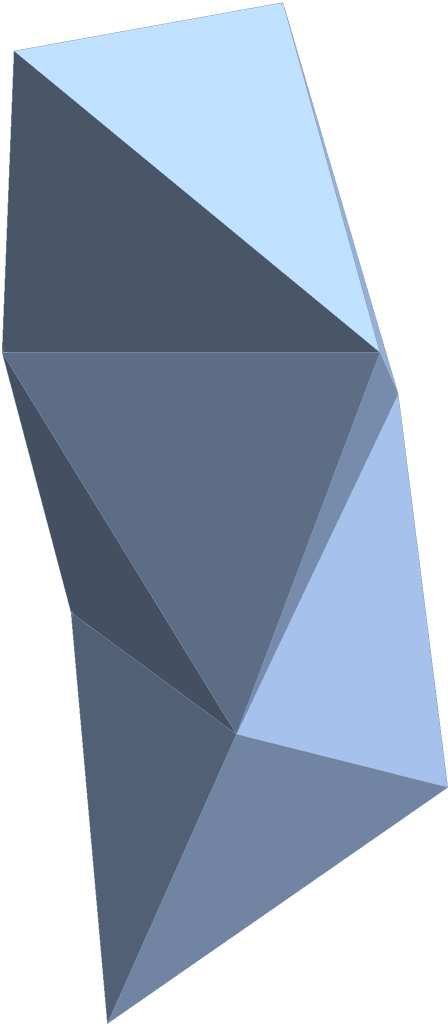
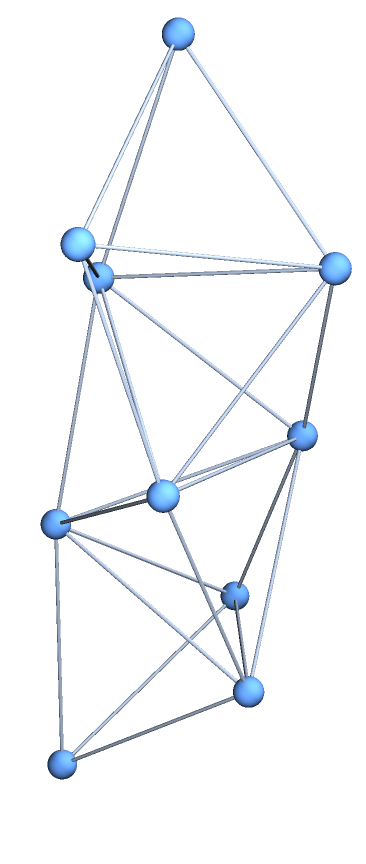
Use MeshConnectivityGraph to obtain a Graph representation of the tetrahelix:

In[7]:=
MeshConnectivityGraph[ResourceFunction["TetrahelixMesh"][7, -1]]
Out[7]=

The tetrahelix can be inscribed inside a cylinder with radius , and a cylinder of radius can be inscribed in the helix:

In[8]:=
With[{n = 8}, Show[Graphics3D[{Opacity[1/2], Cylinder[{{0, 0, 1/Sqrt[10]}, {0, 0, (n + 3)/Sqrt[10]}}, Sqrt[27]/ 10], Cylinder[{{0, 0, 1/Sqrt[10]}, {0, 0, (n + 3)/Sqrt[10]}}, ( 3 Sqrt[2])/20]}], ResourceFunction["TetrahelixMesh"][n, MeshCellStyle -> Opacity[1/2], PlotTheme -> {"Web", "SphereAndTube"}], Boxed -> False]]
Out[8]=

Neat Examples (1) 

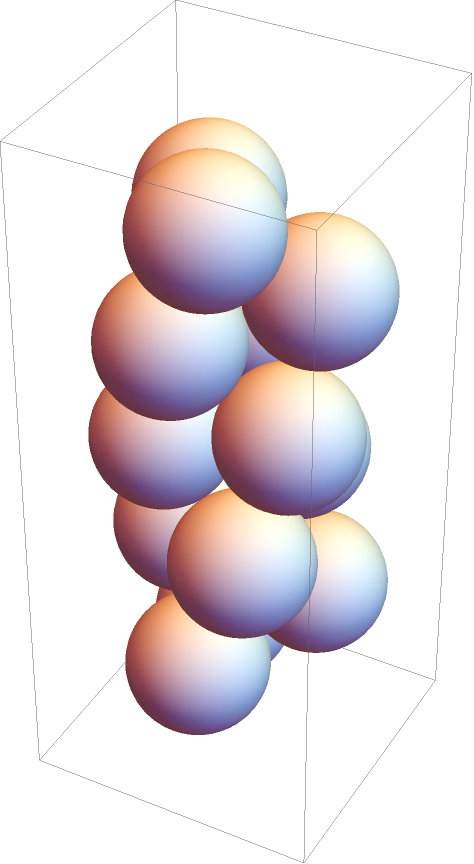
Visualize a helical sphere packing:

In[9]:=
With[{n = 10}, Graphics3D[ Sphere[MeshCoordinates[ResourceFunction["TetrahelixMesh"][n]], 1/2]]]
Out[9]=

Version History

  • 1.0.0 – 21 June 2021

License Information