Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Given a metric, convert between covariant and contravariant components of a tensor
ResourceFunction["TensorIndexJuggling"][tensor,metric] uses metric to convert tensor, having only covariant components (lower indices), into the corresponding tensor with all contravariant components (upper indices). | |
ResourceFunction["TensorIndexJuggling"][tensor,metric,"From"→"AllContravariant","To"→"AllCovariant"] converts tensor, having only contravariant components, into the corresponding tensor with all covariant components. | |
ResourceFunction["TensorIndexJuggling"][tensor,metric,"From"→spec1,"To"→spec2] transforms between upper and lower indices as indicated by "From" and "To". |
Transform a covariant rank-2 tensor in a cylindrical coordinate system to its contravariant form tij→tij:
| In[1]:= | ![ResourceFunction["TensorIndexJuggling"][\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
RowBox[{"8", " ",
RowBox[{"Sin", "[",
RowBox[{"2", " ", "\[Phi]"}], "]"}]}],
RowBox[{
FractionBox["1", "2"], " ", "r", " ",
RowBox[{"Cos", "[",
RowBox[{"2", " ", "\[Phi]"}], "]"}]}],
RowBox[{"3", " ",
RowBox[{"Cos", "[", "\[Phi]", "]"}]}]},
{
RowBox[{
FractionBox["1", "2"], " ", "r"}],
RowBox[{
FractionBox["11", "2"], " ",
SuperscriptBox["r", "2"], " "}],
RowBox[{"r", " ", "8", " ",
RowBox[{"Cos", "[", "\[Phi]", "]"}]}]},
{
RowBox[{"5", " ",
RowBox[{"Cos", "[", "\[Phi]", "]"}]}],
RowBox[{"5", " ", "r", " ",
RowBox[{"Sin", "[", "\[Phi]", "]"}]}], "2"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\), \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "0", "0"},
{"0",
SuperscriptBox["r", "2"], "0"},
{"0", "0", "1"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/1dc8e448ea08530d.png) |
| Out[1]= | 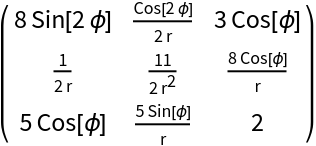 |
Transform a covariant rank-2 tensor in cylindrical coordinates to its mixed form tij→tij:
| In[2]:= | ![ResourceFunction["TensorIndexJuggling"][({
{8 Sin[2 \[Phi]], 1/2 r Cos[2 \[Phi]], 3 Cos[\[Phi]]},
{1/2 r, (11/2) (r^2) , r 8 Cos[\[Phi]]},
{5 Cos[\[Phi]], 5 r Sin[\[Phi]], 2}
}), \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "0", "0"},
{"0",
SuperscriptBox["r", "2"], "0"},
{"0", "0", "1"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\), "From" -> "AllCovariant", "To" -> {"Cov", "Con"}] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/5796ddd11e6f996b.png) |
| Out[3]= | 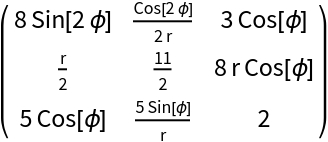 |
Convert tij→tij for a SymmetrizedArray:
| In[4]:= | ![ResourceFunction["TensorIndexJuggling"][
SymmetrizedArray[{{1, 1} -> Subscript[\[Sigma], 11], {1, 2} -> Subscript[\[Sigma], 12], {2, 2} -> Subscript[\[Sigma], 22]}, {2, 2}, Symmetric[{1, 2}]], \!\(\*
TagBox[
RowBox[{"\[IndentingNewLine]",
RowBox[{"CoordinateChartData", "[",
RowBox[{"\"\<Polar\>\"", ",", " ", "\"\<Metric\>\"", ",",
RowBox[{"{",
RowBox[{"r", ",", "\[Phi]"}], "}"}]}], "]"}]}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)
]](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/7e9bbb4caf9fa3f6.png) |
| Out[4]= |
Attempting the conversion tij→tij changes nothing:
| In[5]:= | ![ResourceFunction["TensorIndexJuggling"][\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
RowBox[{"8", " ",
RowBox[{"Sin", "[",
RowBox[{"2", " ", "\[Phi]"}], "]"}]}],
RowBox[{
FractionBox["1", "2"], " ", "r", " ",
RowBox[{"Cos", "[",
RowBox[{"2", " ", "\[Phi]"}], "]"}]}],
RowBox[{"3", " ",
RowBox[{"Cos", "[", "\[Phi]", "]"}]}]},
{
RowBox[{
FractionBox["1", "2"], " ", "r"}],
RowBox[{
FractionBox["11", "2"], " ",
SuperscriptBox["r", "2"], " "}],
RowBox[{"r", " ", "8", " ",
RowBox[{"Cos", "[", "\[Phi]", "]"}]}]},
{
RowBox[{"5", " ",
RowBox[{"Cos", "[", "\[Phi]", "]"}]}],
RowBox[{"5", " ", "r", " ",
RowBox[{"Sin", "[", "\[Phi]", "]"}]}], "2"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\), \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "0", "0"},
{"0",
SuperscriptBox["r", "2"], "0"},
{"0", "0", "1"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\), "To" -> "AllCovariant"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/613cbe80b9b2bf76.png) |
| Out[8]= | 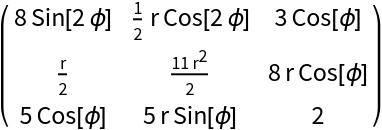 |
Start with a covariant base:
| In[9]:= |
Get the contravariant base through raising the index:
| In[10]:= | ![gCon = (ResourceFunction["TensorIndexJuggling"][{g1, g2, g3},
CoordinateChartData["Cylindrical", "Metric", {r, \[Phi], z}]]) /. {g1 -> gCov[[1]], g2 -> gCov[[2]], g3 -> gCov[[3]]} // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/38ec35169921a675.png) |
| Out[10]= |
Check the orthonormality relationship gi·gj=δij:
| In[11]:= | ![Simplify@( {
{gCov[[1]] . gCon[[1]], gCov[[1]] . gCon[[2]], gCov[[1]] . gCon[[3]]},
{gCov[[2]] . gCon[[1]], gCov[[2]] . gCon[[2]], gCov[[2]] . gCon[[3]]},
{gCov[[3]] . gCon[[1]], gCov[[3]] . gCon[[2]], gCov[[3]] . gCon[[3]]}
} ) // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/778f6e48498d5dde.png) |
| Out[11]= |
Start with the metric for cylindrical coordinates in Euclidean space:
| In[12]:= |
| Out[10]= | 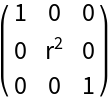 |
Get the contravariant components of the metric:
| In[13]:= |
| Out[11]= | 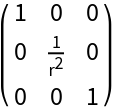 |
This result is the same as the Wolfram Language built-in function:
| In[14]:= |
| Out[15]= | 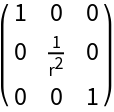 |
| In[16]:= |
| Out[17]= |
Start with the metric for cylindrical coordinates in Euclidean space:
| In[18]:= |
| Out[73]= | 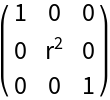 |
Define a Cartesian rank-2 tensor:
| In[74]:= |
| Out[75]= |
Contract the indices:
| In[76]:= |
| Out[76]= |
Use the resource function TensorCoordinateTransform to transform t to cylindrical coordinates with covariant transformation behavior tij:
| In[77]:= | ![tInCylCovCov = ResourceFunction["TensorCoordinateTransform"][
t, (CoordinateTransformData["Cylindrical" -> "Cartesian", "MappingJacobian", {r, \[Phi], z}])\[Transpose], "TransformationBehavior" -> "AllCovariant"] // Simplify[#, r > 0] &;
tInCylCovCov // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/46e5916d15a082bc.png) |
| Out[129]= | 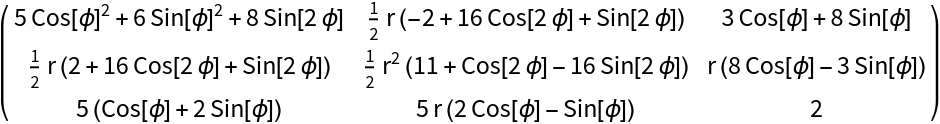 |
Contraction should not be invariant:
| In[130]:= |
| Out[130]= |
But contraction of opposing indices should be:
| In[131]:= | ![TensorContract[
ResourceFunction["TensorIndexJuggling"][tInCylCovCov, metricCyl, "To" -> {"Cov", "Con"}],
{1, 2}] // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/4e45c9c4ffd066f2.png) |
| Out[131]= |
Start with a rank-6 tensor in a Cartesian basis and form the contraction tijkijkl:
| In[132]:= | ![SeedRandom[3141]
t = RandomInteger[{-10, 10}, {3, 3, 3, 3, 3, 3}];
TensorContract[t, {{1, 4}, {2, 5}, {3, 6}}]](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/7b5265d41d5ccaf0.png) |
| Out[132]= |
Transform to an different affine system with given mapping:
| In[133]:= | ![tAllCov = ResourceFunction["TensorCoordinateTransform"][t, mapping = ( {
{2, 3, 1},
{1, 2, 2},
{1, 0, 1}
} ), "TransformationBehavior" -> "AllContravariant"];](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/2316cd4b0dd330e7.png) |
Contraction of the indices of the same type does not lead to an invariant:
| In[134]:= |
| Out[134]= |
Contraction of the right opposing index pairs, after index juggling, leads to the same result as in the original coordinate system:
| In[135]:= | ![TensorContract[
tConConConCovCovCov = ResourceFunction["TensorIndexJuggling"][tAllCov, metric = ( {
{mapping[[1]] . mapping[[1]], mapping[[1]] . mapping[[2]], mapping[[1]] . mapping[[3]]},
{mapping[[2]] . mapping[[1]], mapping[[2]] . mapping[[2]], mapping[[2]] . mapping[[3]]},
{mapping[[3]] . mapping[[1]], mapping[[3]] . mapping[[2]], mapping[[3]] . mapping[[3]]}
} ), "From" -> "AllContravariant", "To" -> {"Con", "Con", "Con", "Cov", "Cov", "Cov"}],
{{1, 4}, {2, 5}, {3, 6}}]](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/6ff1fc14474c2792.png) |
| Out[135]= |
If the mapping rule between the two coordinate frames exists, index juggling can also be done using the resource function TensorCoordinateTransform. However, if only the metric of the space is available, then TensorIndexJuggling is recommended:
| In[136]:= | ![(ResourceFunction["TensorCoordinateTransform"][
t = RandomInteger[{-10, 10}, {3, 3, 3, 3, 3, 3}], mapping = ( {
{2, 3, 1},
{1, 2, 2},
{1, 0, 1}
} ), "TransformationBehavior" -> {"Cov", "Con", "Cov", "Con", "Cov", "Con"}]) == (ResourceFunction["TensorIndexJuggling"][
ResourceFunction["TensorCoordinateTransform"][t, mapping, "TransformationBehavior" -> "AllCovariant"], ( {
{mapping[[1]] . mapping[[1]], mapping[[1]] . mapping[[2]], mapping[[1]] . mapping[[3]]},
{mapping[[2]] . mapping[[1]], mapping[[2]] . mapping[[2]], mapping[[2]] . mapping[[3]]},
{mapping[[3]] . mapping[[1]], mapping[[3]] . mapping[[2]], mapping[[3]] . mapping[[3]]}
} ), "To" -> {"Cov", "Con", "Cov", "Con", "Cov", "Con"}])](https://www.wolframcloud.com/obj/resourcesystem/images/2f1/2f16f302-8c62-4573-ac9f-83b8effc0dbc/54de9f24c6aa391c.png) |
| Out[136]= |
This work is licensed under a Creative Commons Attribution 4.0 International License