Function Repository Resource:

TangentPlane

Find the tangent plane of a function at a point

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["TangentPlane"][expr,{x,a},{y,b},z]

returns an association of properties of the tangent plane to expr, viewed as an equation in x,y and z, at the point x=a,y=b.

ResourceFunction["TangentPlane"][expr,{x,a},{y,b},{z,c},w]

returns properties of a tangent plane in four dimensions.

ResourceFunction["TangentPlane"][…,prop]

returns the value of the tangent plane property prop.

Details

Allowed values of prop are "StandardFormEquation", "Slopes" and "Plot".

If expr does not have head Equal, then expr is treated as an expression defining the independent variable in terms of the dependent variables. In other words, ResourceFunction["TangentPlane"][expr,{x,a},{y,b},z] is equivalent to ResourceFunction["TangentPlane"][z==expr,{x,a},{y,b},z] if expr itself has a head other than Equal, and similarly in four dimensions.

Examples

Basic Examples (2)

Return the equation of the tangent plane to a surface:

In[1]:=

$ResourceFunction[ "TangentPlane", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ x^2 + y^2, {x, 2}, {y, 3}, z, "StandardFormEquation"]$

Out[1]=

Visualize the tangent plane:

In[2]:=

$ResourceFunction[ "TangentPlane", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][x^2 + y^2, {x, 2}, {y, 3}, z, "Plot"]$

Out[2]=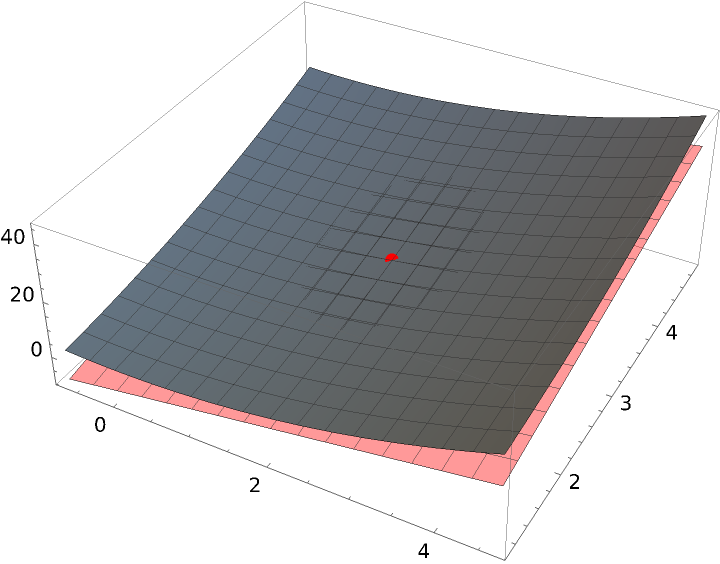

Compute the slopes of the tangent plane with respect to x and y:

In[3]:=

$ResourceFunction[ "TangentPlane", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][x^2 + y^2, {x, 2}, {y, 3}, z, "Slopes"]$

Out[3]=

Get an association of properties of a tangent plane to a surface:

In[4]:=

Out[4]=

Scope (2)

The first argument to TangentPlane can be an implicit definition of a surface:

In[5]:=

$ResourceFunction[ "TangentPlane", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ x^2 + y^2 + z^2 == 9, {x, 0}, {y, 0}, {z, -3}, "Plot"]$

Out[5]=

TangentPlane also can return equations or slopes of surfaces defined in 4 dimensions:

In[6]:=

$ResourceFunction[ "TangentPlane", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ w == x^2 + y^2 + z^2, {x, 2}, {y, 3}, {z, 5}, w]$