Function Repository Resource:

TangentLine (4.0.0) current version: 5.1.0 »

Source Notebook

Compute properties of the tangent line to a curve at a given point

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["TangentLine"][expr,{x,a},{y,b}]

gives an association of properties of the tangent line to expr, viewed as an equation in x and y, at the point {x,y}={a,b}.

ResourceFunction["TangentLine"][expr,{x,a},{y,b},prop]

returns the value of the tangent line property prop.

ResourceFunction["TangentLine"][expr,{x,a},y]

returns information relating to one, among possibly several, of the tangent lines to expr at x=a.

ResourceFunction["TangentLine"][expr,x,{y,b}]

returns information relating to one, among possibly several, of the tangent lines to expr at y=b.

Details

Allowed values of prop are:

"SlopeInterceptEquation"

equation of the tangent line in slope intercept form

"StandardFormEquation"

equation of the tangent line in standard form

"PointSlopeEquation"

equation of the tangent line in point slope form

"HorizontalIntercept"

horizontal intercept for the tangent line equation

"VerticalIntercept"

vertical intercept for the tangent line equation

"Plot"

plot of the tangent line equation

All

association of information returning all allowed properties

If expr does not have head Equal, then expr is treated as an expression defining y in terms of x. In other words, ResourceFunction["TangentLine"][expr,{x,a},y,…] is equivalent to ResourceFunction["TangentLine"][y==expr,{x,a},y,…] if expr has a head other than Equal.

If only one coordinate of the intersection point is given, the other coordinate is inferred. For expressions that are multivalued at the given value of x or y, information on only one of potentially several tangent lines is returned.

Examples

Basic Examples (2)

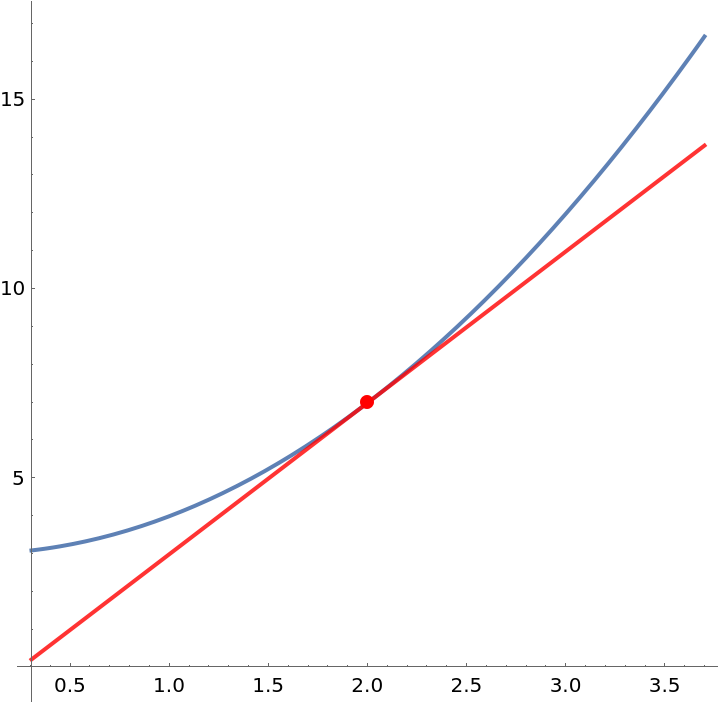
Compute the slope-intercept equation of the tangent line to a curve at a given point:

In[1]:=

$ResourceFunction["TangentLine"][ y == x^2 + 3, {x, 2}, y, "SlopeInterceptEquation"]$

Out[1]=

Visualize this result:

In[2]:=

$ResourceFunction["TangentLine"][y == x^2 + 3, {x, 2}, y, "Plot"]$

Out[2]=

Compute the slope of this tangent line:

In[3]:=

$ResourceFunction["TangentLine"][y == x^2 + 3, {x, 2}, y, "Slope"]$

Out[3]=

Compute the horizontal intercept of this tangent line:

In[4]:=

$ResourceFunction["TangentLine"][ y == x^2 + 3, {x, 2}, y, "HorizontalIntercept"]$

Out[4]=

Get the standard-form equation of this tangent line:

In[5]:=

$ResourceFunction["TangentLine"][ y == x^2 + 3, {x, 2}, y, "StandardFormEquation"]$

Out[5]=

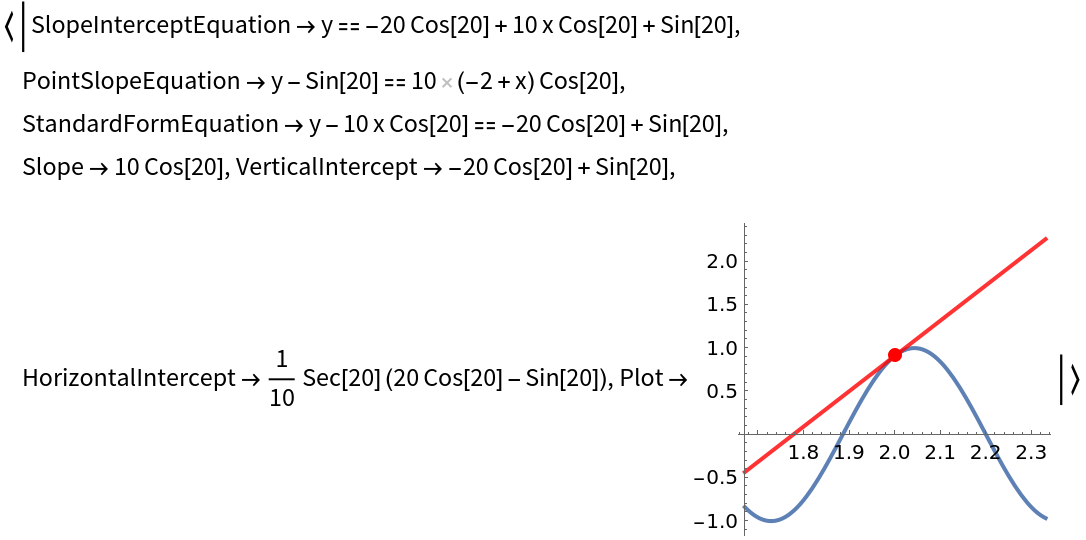
Get an association of properties of a tangent line to a curve:

In[6]:=

Out[6]=

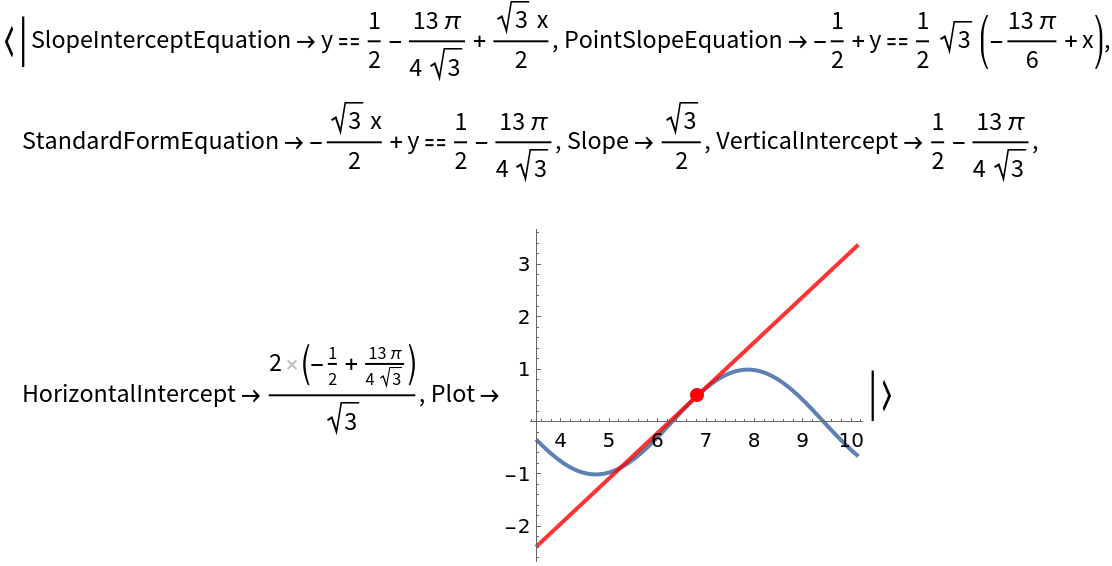
Get just the point-slope equation of this tangent line:

In[7]:=

Out[7]=

Scope (1)

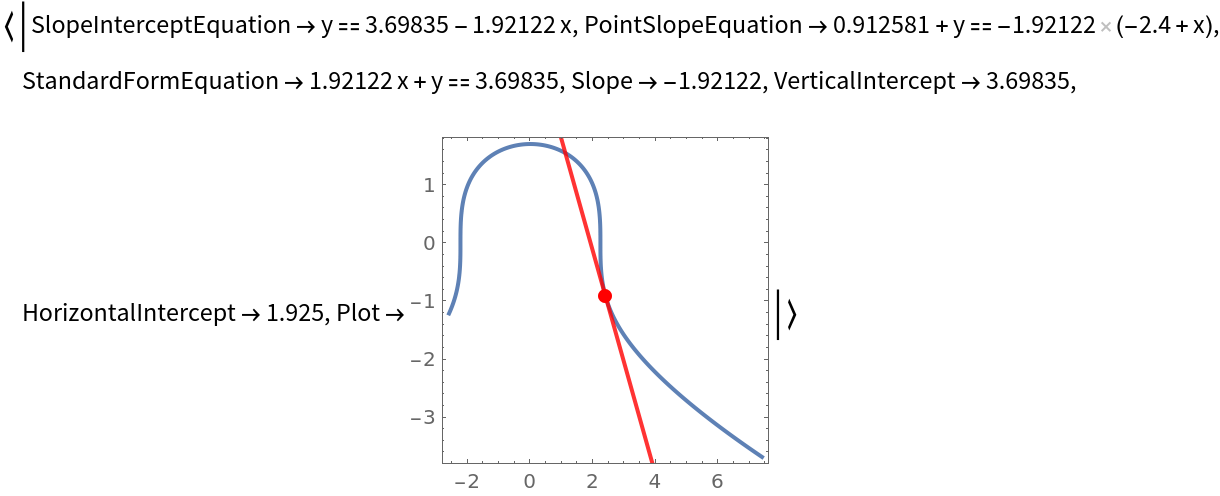
The first argument to TangentLine can be an implicit definition of a curve:

In[8]:=

$ResourceFunction["TangentLine"][x^2 + y^3 == 5, {x, 2.4}, y]$

Out[8]=

Properties and Relations (2)

If a tangent line is parallel to a coordinate axis, its intercept with that axis is None:

In[9]:=

$ResourceFunction["TangentLine"][ x^2 + 3, {x, 0}, y, "HorizontalIntercept"]$

Out[9]=

Requesting tangent line information about a point that is not on the curve will result in an error message:

In[10]:=

Out[10]=

Possible Issues (2)

If a position for y is not specified, information on only one of the possible normal lines at the given x-value is returned:

In[11]:=

Out[11]=

Vertical tangent lines (whose slope cannot be computed) are plotted as dotted lines. Some of their properties may not be defined:

In[12]:=

$ResourceFunction["TangentLine"][x^2 + y^2 == 1, {x, 1}, {y, 0}]$

Out[12]=

If a function has a cusp or a discontinuity at the given point, no tangent line is returned:

In[13]:=

Out[13]=

Related Links

Version History

5.1.0 – 04 August 2023
5.0.0 – 23 March 2023
4.0.1 – 28 March 2022
4.0.0 – 26 May 2021
3.0.0 – 24 January 2020
2.0.0 – 06 September 2019
1.0.0 – 23 August 2019

Related Resources

Author Notes

To view the full source code for TangentLine, evaluate the following:

In[1]:=

SystemOpen[
FileNameJoin[{DirectoryName[FindFile["ResourceFunctionHelpers`"]], "TangentAndNormalLine.wl"}]]

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License