Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute properties of the tangent and normal lines to a curve at a given point
ResourceFunction["TangentAndNormalLine"][expr,{x,a},{y,b}] gives an association of properties of the tangent and normal lines to expr, viewed as an equation in x and y, at the point {x,y}={a,b}. | |
ResourceFunction["TangentAndNormalLine"][expr,{x,a},{y,b},prop] returns the value of the tangent and normal lines property prop. | |
ResourceFunction["TangentAndNormalLine"][expr,{x,a},y] returns information relating to one pair, among possibly several, of the tangent and normal lines to expr at x=a. | |
ResourceFunction["TangentAndNormalLine"][expr,x,{y,b}] returns information relating to one pair, among possibly several, of the tangent and normal lines to expr at y=b. |
| "SlopeInterceptEquation" | equation of the tangent line in slope intercept form |
| "StandardFormEquation" | equation of the tangent line in standard form |
| "PointSlopeEquation" | equation of the tangent line in point slope form |
| "HorizontalIntercept" | horizontal intercept for the tangent line equation |
| "VerticalIntercept" | vertical intercept for the tangent line equation |
| "Plot" | plot of the tangent line equation |
| All | association of information returning all allowed properties |
Compute the slope-intercept equations of the tangent and normal lines to a curve at a given point:
| In[1]:= |
| Out[1]= |
Visualize this result:
| In[2]:= |
| Out[2]= | 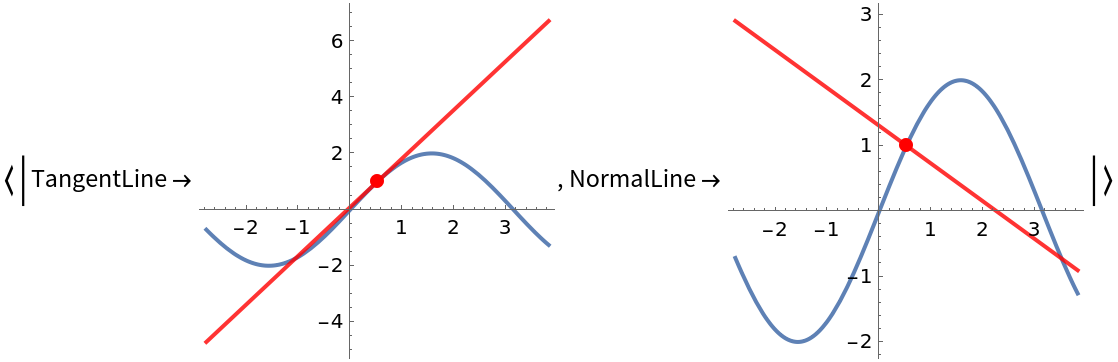 |
Compute the slope of these tangent and normal lines:
| In[3]:= |
| Out[3]= |
Compute the horizontal intercepts of these tangent and normal lines:
| In[4]:= |
| Out[4]= |
Get the standard-form equation of these tangent and normal lines:
| In[5]:= |
| Out[5]= |
Get an association of properties of the tangent and normal lines to a curve:
| In[6]:= |
| Out[6]= | 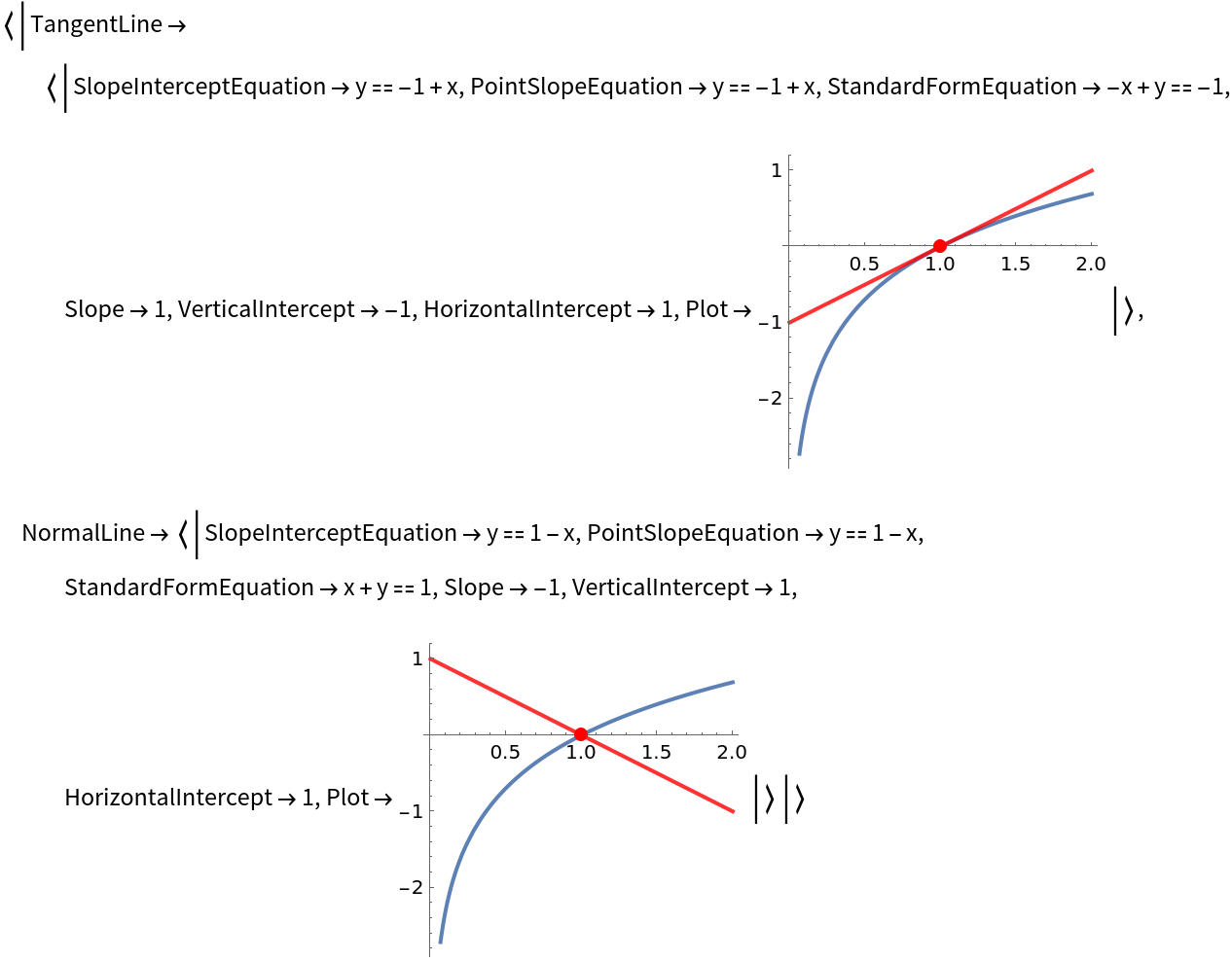 |
Get just the point-slope equations:
| In[7]:= |
| Out[7]= |
The first argument to TangentAndNormalLine can be an implicit definition of a curve:
| In[8]:= |
| Out[8]= | 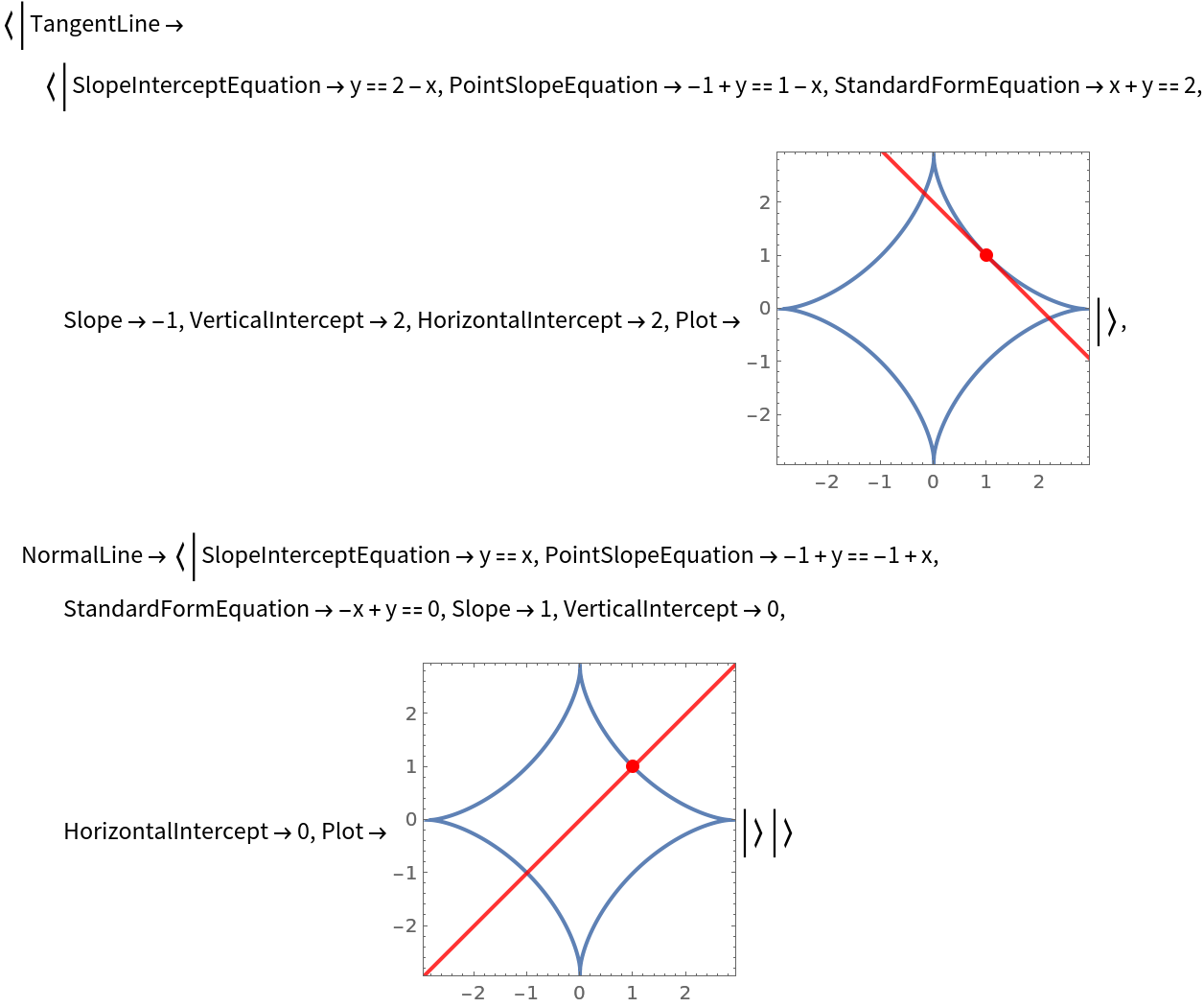 |
If a tangent or normal line is parallel to a coordinate axis, its intercept with that axis is None:
| In[9]:= |
| Out[9]= |
If a position for y is not specified, information on only one of the possible normal lines at the given x value is returned:
| In[10]:= |
| Out[10]= | 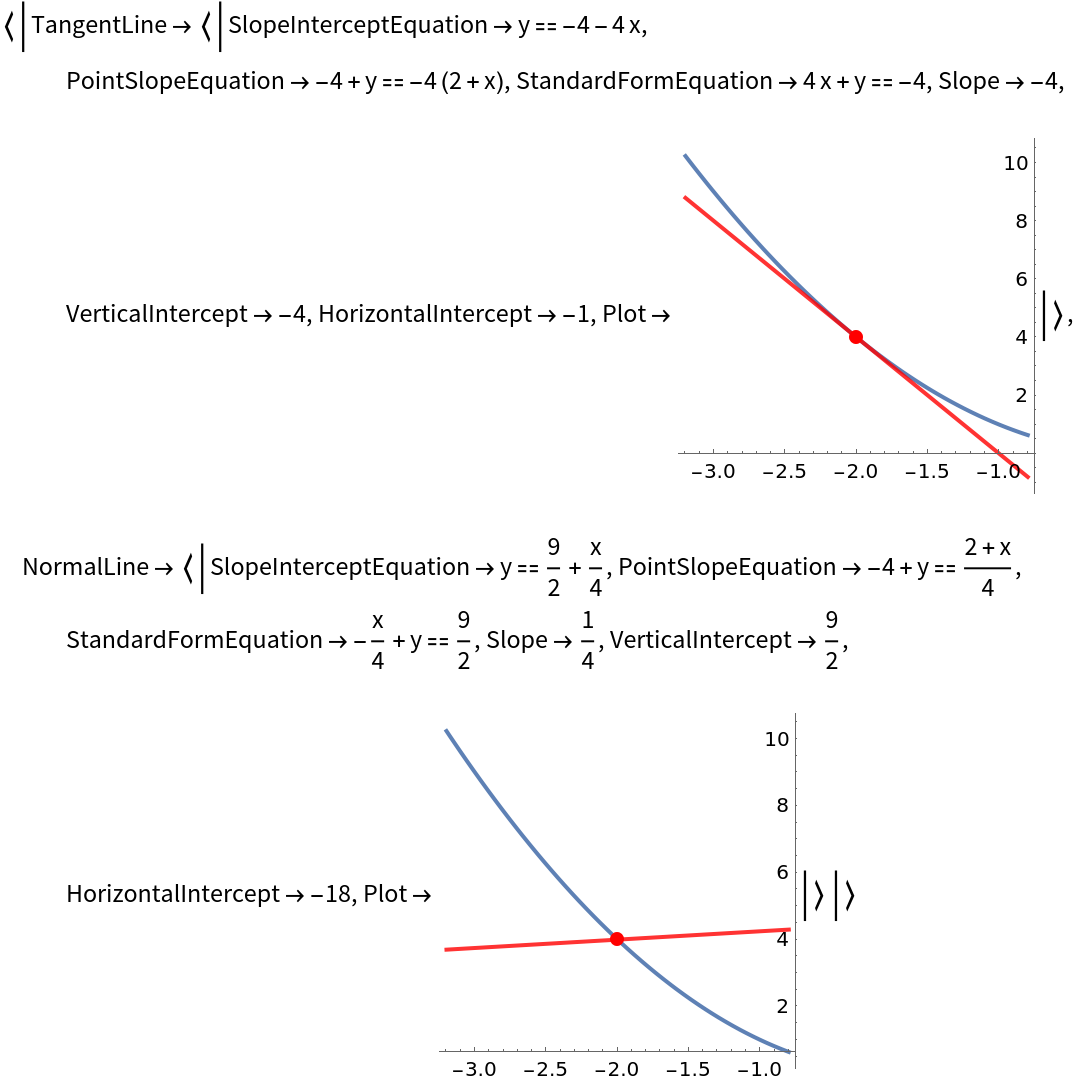 |
Requesting tangent and normal lines information about a point that is not on the curve will result in an error message:
| In[11]:= |
| Out[11]= |
Vertical tangent lines (whose slope cannot be computed) are plotted as dotted lines. Some of their properties may not be defined:
| In[12]:= |
| Out[12]= | 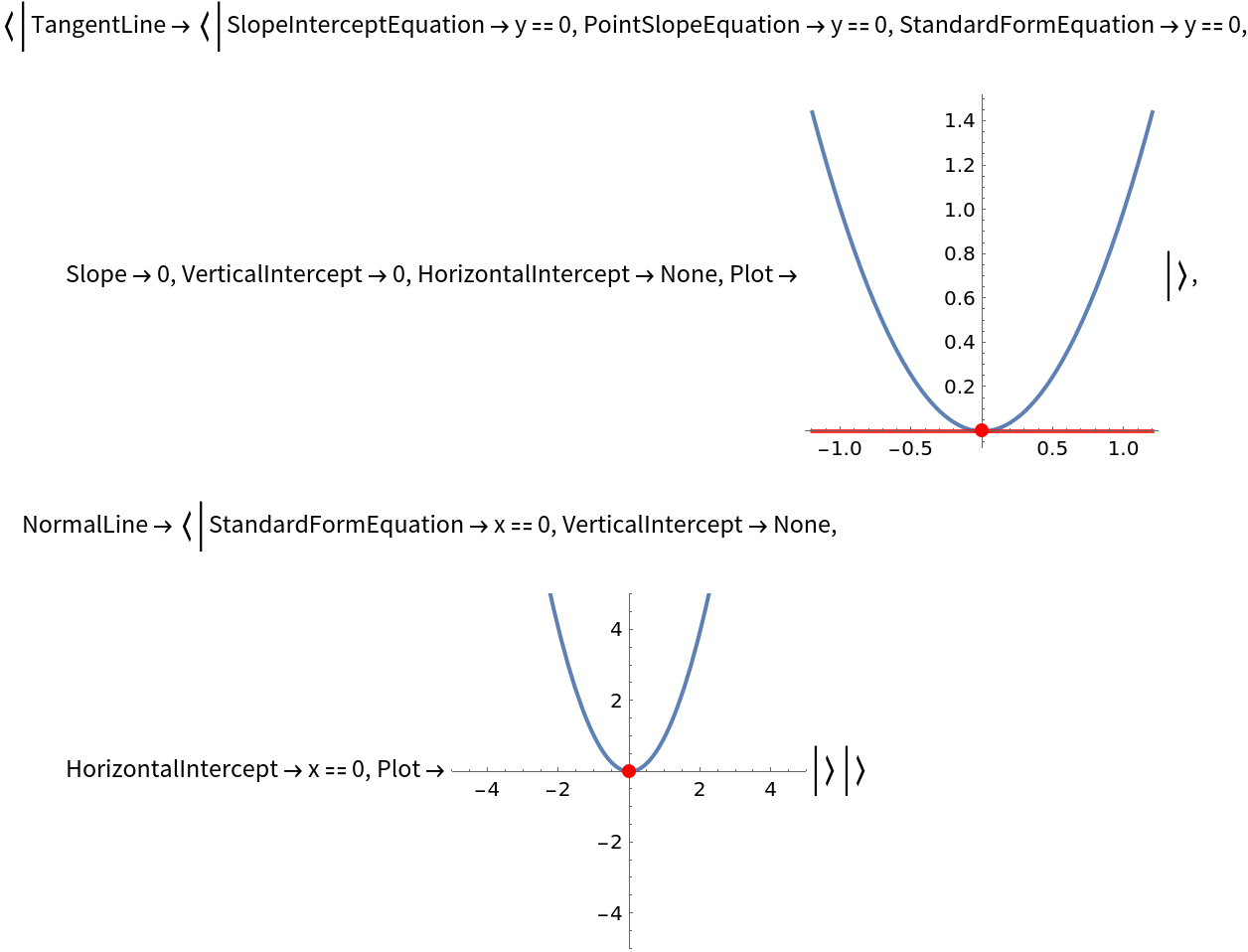 |
If a function has a cusp or a discontinuity at the given point, no tangent or normal line is returned:
| In[13]:= |
| Out[13]= |
This work is licensed under a Creative Commons Attribution 4.0 International License