Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Takagi function
ResourceFunction["TakagiT"][x] gives the Takagi function T(x). |
Plot the Takagi function:
| In[1]:= |
| Out[1]= | 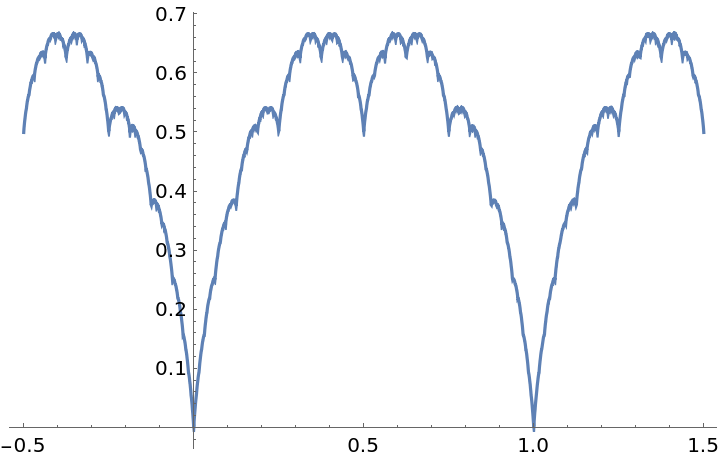 |
Evaluate at integers or rationals:
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= |
Evaluate at inexact real numbers:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |
Parity transformation is automatically applied:
| In[6]:= |
| Out[6]= |
TakagiT threads elementwise over lists:
| In[7]:= |
| Out[7]= |
Compare the Takagi function with a sum of the successive iterates of the tent map:
| In[8]:= |
| In[9]:= | ![With[{n = 9}, Plot[{ResourceFunction["TakagiT"][x], Total[Rest[NestList[tent, x, n]]/2^Range[n]]}, {x, 0, 1}, {PlotLegends -> {"Takagi function", "tent map approximation"}, PlotStyle -> {
Thickness[0.015],
Thickness[0.008]}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/5bd/5bd790ff-a0f2-40af-a8a4-4179813286db/127487e4090e509f.png) |
| Out[9]= | 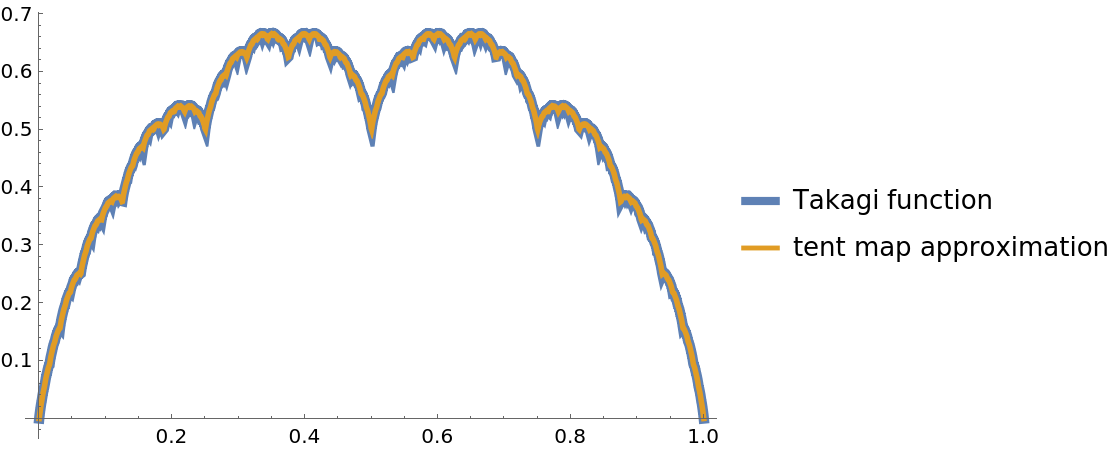 |
Compare the Takagi function with its Fourier series approximation:
| In[10]:= | ![cc[0] = 1/2;
cc[n_Integer] := Module[{an = Abs[n], r},
r = BitShiftRight[an, IntegerExponent[an, 2]];
-1/(Pi^2 an r)]](https://www.wolframcloud.com/obj/resourcesystem/images/5bd/5bd790ff-a0f2-40af-a8a4-4179813286db/63f5e43070fced75.png) |
| In[11]:= |
| Out[11]= |  |
The Takagi function satisfies the reflection identity T(1-x)=T(x) for 0≤x≤1:
| In[12]:= |
| Out[12]= |  |
The Takagi function satisfies the self-similarity identity T(x/2)=x/2+T(x)/2 for 0≤x≤1:
| In[13]:= |
| Out[13]= | 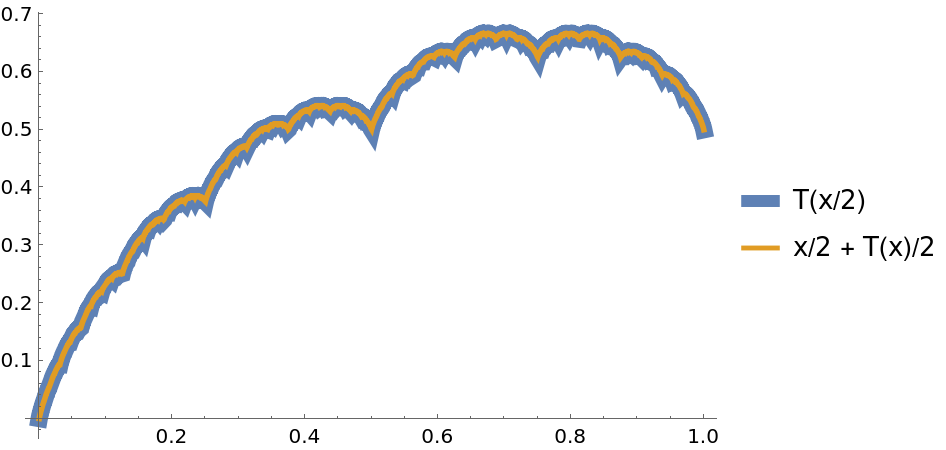 |
This work is licensed under a Creative Commons Attribution 4.0 International License