Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 TakagiDecomposition

Source Notebook

Compute the Takagi decomposition of a complex-symmetric matrix

Contributed by: Jan Mangaldan

ResourceFunction["TakagiDecomposition"][m]

gives the Takagi decomposition for a complex-symmetric numerical matrix m as a list of matrices {q,d} where q is a unitary matrix and d is a diagonal matrix.

Details

The Takagi decomposition is also known as the Autonne-Takagi decomposition.
The matrix m must be square and complex-symmetric (as opposed to Hermitian). That is, m==Transpose[m].
The original matrix m is equal to q.d.Transpose[q].
The diagonal elements of d are real and non-negative.

Examples

Basic Examples (3) 

Find the Takagi decomposition of a complex-symmetric matrix:

In[1]:=
m = N@\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { RowBox[{"3", "+", RowBox[{"24", " ", "I"}]}], RowBox[{ RowBox[{"-", "4"}], "-", RowBox[{"6", " ", "I"}]}], RowBox[{"8", "+", RowBox[{"12", " ", "I"}]}]}, { RowBox[{ RowBox[{"-", "4"}], "-", RowBox[{"6", " ", "I"}]}], RowBox[{"2", "+", RowBox[{"16", " ", "I"}]}], RowBox[{"18", "-", RowBox[{"12", " ", "I"}]}]}, { RowBox[{"8", "+", RowBox[{"12", " ", "I"}]}], RowBox[{"18", "-", RowBox[{"12", " ", "I"}]}], RowBox[{"1", "+", RowBox[{"8", " ", "I"}]}]} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\);
In[2]:=
{q, d} = ResourceFunction["TakagiDecomposition"][m]
Out[2]=

Confirm the decomposition up to numerical rounding:

In[3]:=
m - q . d . Transpose[q] // Chop
Out[3]=

Format q and d:

In[4]:=
{q // MatrixForm, d // MatrixForm}
Out[4]=

Scope (3) 

A complex-symmetric matrix with arbitrary-precision entries:

In[5]:=
m = RandomVariate[NormalDistribution[], 3, WorkingPrecision -> 20] . RandomVariate[CircularOrthogonalMatrixDistribution[3], 3, WorkingPrecision -> 20]
Out[5]=

Find the Takagi decomposition:

In[6]:=
{q, d} = ResourceFunction["TakagiDecomposition"][m]
Out[6]=

Confirm the decomposition up to numerical rounding:

In[7]:=
m - q . d . Transpose[q] // Chop
Out[7]=

Properties and Relations (2) 

Generate a complex-symmetric matrix:

In[8]:=
m = RandomVariate[NormalDistribution[], 2] . RandomVariate[CircularOrthogonalMatrixDistribution[3], 2]
Out[8]=

Compute its Takagi decomposition:

In[9]:=
{q, d} = ResourceFunction["TakagiDecomposition"][m]
Out[9]=

q is a unitary matrix:

In[10]:=
ConjugateTranspose[q] . q // Chop
Out[10]=

d is a diagonal matrix with non-negative entries:

In[11]:=
DiagonalMatrixQ[d] && AllTrue[Diagonal[d], NonNegative]
Out[11]=

m is equal to q.d.Transpose[q]:

In[12]:=
m - q . d . Transpose[q] // Chop
Out[12]=

For real symmetric positive-definite matrices, TakagiDecomposition gives a result equivalent to SingularValueDecomposition and SchurDecomposition:

In[13]:=
m = N@HilbertMatrix[3];
In[14]:=
{qt, dt} = ResourceFunction["TakagiDecomposition"][m]
Out[14]=
In[15]:=
m - qt . dt . Transpose[qt] // Chop
Out[15]=
In[16]:=
{qs, ts} = SchurDecomposition[m]
Out[16]=
In[17]:=
m - qs . ts . Transpose[qs] // Chop
Out[17]=
In[18]:=
{us, ds} = Most[SingularValueDecomposition[m]]
Out[18]=
In[19]:=
m - us . ds . Transpose[us] // Chop
Out[19]=

Possible Issues (1) 

TakagiDecomposition only works with approximate numerical matrices:

In[20]:=
ResourceFunction[ "TakagiDecomposition"][{{-54, 16 I, 112 I, -28}, {16 I, -36, -52, -88 I}, {112 I, -52, -114, -16 I}, {-28, -88 I, -16 I, -96}}]
Out[20]=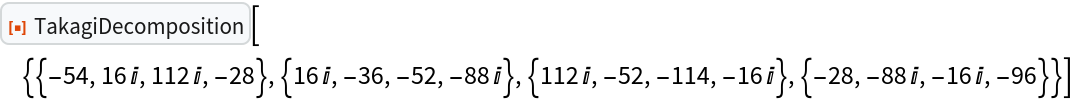
In[21]:=
ResourceFunction["TakagiDecomposition"][ N[{{-54, 16 I, 112 I, -28}, {16 I, -36, -52, -88 I}, {112 I, -52, -114, -16 I}, {-28, -88 I, -16 I, -96}}]]
Out[21]=

Version History

  • 1.0.0 – 13 March 2023

Source Metadata

  • Citation:
    • Autonne L., "Sur les matrices hypohermitiennes et sur les matrices unitaires." Annales de l'Université de Lyon, vol. 38, 1–77, 1915.
      Available from       https://gallica.bnf.fr/ark:/12148/bpt6k69553b
    • Chebotarev A.M., Teretenkov A.E., "Singular value decomposition for the Takagi factorization of symmetric matrices." Applied Mathematics and Computation, vol. 234, 380–384, 2014.
      DOI: 10.1016/j.amc.2014.01.170
    • Takagi T., "On an Algebraic Problem Related to an Analytic Theorem of Carathéodory and Fejér and on an Allied Theorem of Landau." Japanese Journal of Mathematics, vol. 1, 83–93, 1924.
      DOI: 10.4099/jjm1924.1.0_83

Related Resources

License Information