Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SymmetricKroneckerProduct

Source Notebook

Calculate the symmetric Kronecker product of two matrices

Contributed by: Jan Mangaldan

ResourceFunction["SymmetricKroneckerProduct"][m1,m2]

constructs the symmetric Kronecker product of the square matrices m1 and m2.

Details

The symmetric Kronecker product is a variation of the Kronecker product that is commutative, and is often used in the theory of semidefinite programming, and algorithms for solving semidefinite programs.
The square matrices m1 and m2 must have the same dimensions.
If m1 and m2 are both of length n, then the symmetric Kronecker product is a square matrix of length n(n+1)/2.
ResourceFunction["SymmetricKroneckerProduct"] can be used on SparseArray objects, returning a SparseArray object when possible.

Examples

Basic Examples (1) 

Compute the symmetric Kronecker product of two symbolic 2×2 matrices:

In[1]:=
ResourceFunction["SymmetricKroneckerProduct"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { SubscriptBox["\[FormalA]", "11"], SubscriptBox["\[FormalA]", "12"]}, { SubscriptBox["\[FormalA]", "21"], SubscriptBox["\[FormalA]", "22"]} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { SubscriptBox["\[FormalB]", "11"], SubscriptBox["\[FormalB]", "12"]}, { SubscriptBox["\[FormalB]", "21"], SubscriptBox["\[FormalB]", "22"]} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)] // MatrixForm
Out[1]=

Scope (3) 

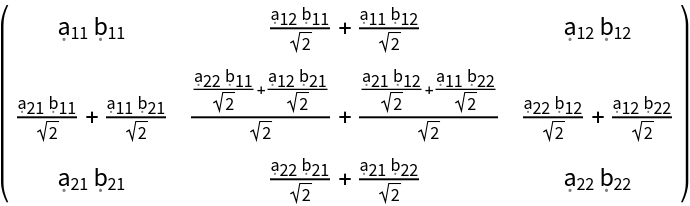The symmetric Kronecker product of two exact matrices:

In[2]:=
ResourceFunction["SymmetricKroneckerProduct"][HilbertMatrix[3], ToeplitzMatrix[3]] // Simplify
Out[2]=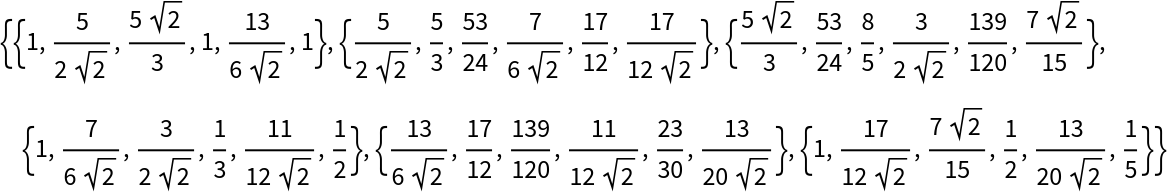

The symmetric Kronecker product of two numerical matrices:

In[3]:=
{m1, m2} = RandomVariate[GaussianUnitaryMatrixDistribution[3], 2]; ResourceFunction["SymmetricKroneckerProduct"][m1, m2]
Out[3]=

The symmetric Kronecker product of two sparse matrices:

In[4]:=
s = SparseArray[{i_, i_} :> i, {4, 4}]; t = SparseArray[{{i_, j_} /; Abs[i - j] == 1 :> i - j}, {4, 4}]; ResourceFunction["SymmetricKroneckerProduct"][s, t]
Out[4]=

Properties and Relations (5) 

The symmetric Kronecker product is multi-linear (linear in each argument):

In[5]:=
ResourceFunction["SymmetricKroneckerProduct"][C[1] m1 + C[2] m2, m3] == C[1] ResourceFunction["SymmetricKroneckerProduct"][m1, m3] + C[2] ResourceFunction["SymmetricKroneckerProduct"][m2, m3] // Simplify
Out[5]=
In[6]:=
ResourceFunction["SymmetricKroneckerProduct"][m1, C[1] m2 + C[2] m3] == C[1] ResourceFunction["SymmetricKroneckerProduct"][m1, m2] + C[2] ResourceFunction["SymmetricKroneckerProduct"][m1, m3] // Simplify
Out[6]=

The symmetric Kronecker product is commutative:

In[7]:=
m1 = Array[\[FormalX], {5, 5}]; m2 = Array[\[FormalY], {5, 5}]; ResourceFunction["SymmetricKroneckerProduct"][m1, m2] == ResourceFunction["SymmetricKroneckerProduct"][m2, m1]
Out[7]=

Transposition distributes over the symmetric Kronecker product:

In[8]:=
m1 = Array[\[FormalX], {5, 5}]; m2 = Array[\[FormalY], {5, 5}]; Transpose[ResourceFunction["SymmetricKroneckerProduct"][m1, m2]] == ResourceFunction["SymmetricKroneckerProduct"][Transpose[m1], Transpose[m2]] // Simplify
Out[8]=

The symmetric Kronecker product distributes over addition:

In[9]:=
ResourceFunction["SymmetricKroneckerProduct"][m1 + m2, m3] == ResourceFunction["SymmetricKroneckerProduct"][m1, m3] + ResourceFunction["SymmetricKroneckerProduct"][m2, m3] // Simplify
Out[9]=

Verify an expansion formula for the product of two symmetric Kronecker products:

In[10]:=
m1 = Array[\[FormalX], {3, 3}]; m2 = Array[\[FormalY], {3, 3}]; m3 = Array[\[FormalZ], {3, 3}]; m4 = Array[\[FormalW], {3, 3}]; ResourceFunction["SymmetricKroneckerProduct"][m1, m2] . ResourceFunction["SymmetricKroneckerProduct"][m3, m4] == 1/2 (ResourceFunction["SymmetricKroneckerProduct"][m1 . m3, m2 . m4] + ResourceFunction["SymmetricKroneckerProduct"][m1 . m4, m2 . m3]) // Simplify
Out[10]=

Version History

  • 1.0.0 – 12 September 2022

Source Metadata

  • Citation:
    • Alizadeh F., Haeberly J.A., Overton M.L., "Primal-Dual Interior-Point Methods for Semidefinite Programming: Convergence Rates, Stability and Numerical Results." SIAM Journal on Optimization, vol. 8, no. 3, 746-768, 1998.
      DOI: 10.1137/S1052623496304700
    • Todd M.J., Toh K.C., Tütüncü R.H., "On the Nesterov-Todd Direction in Semidefinite Programming." SIAM Journal on Optimization, vol. 8, no. 3, 769-796, 1998.
      DOI: 10.1137/S105262349630060X

Related Resources

License Information