Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
The complement of the union and intersection of lists, with duplicates deleted
ResourceFunction["SymmetricDifference"][lists] gives the complement of the Union and Intersection of lists. |
The common element 3 is removed from the Union of the sets:
| In[1]:= |
| Out[1]= |
Define three lists:
| In[2]:= | 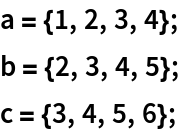 |
Here is their Union:
| In[3]:= |
| Out[3]= |
Here is their Intersection:
| In[4]:= |
| Out[4]= |
Using those, you can define their symmetric difference:
| In[5]:= |
| Out[5]= |
SymmetricDifference gives the same result:
| In[6]:= |
| Out[6]= |
First define four regions:
| In[7]:= | ![{d1, d2, d3, d4} = {
Disk[{1, 1}, 2],
Disk[{1, -1}, 2],
Disk[{-1, -1}, 2],
Disk[{-1, 1}, 2]
};](https://www.wolframcloud.com/obj/resourcesystem/images/a56/a561688e-516a-40db-bbe9-6ae8b61e4807/4f0294583e263374.png) |
The function RegionSymmetricDifference is like the resource function MultisetSymmetricDifference, not SymmetricDifference:
| In[8]:= |
| Out[8]= |  |
This construction is like SymmetricDifference:
| In[9]:= | ![Region@RegionDifference[
RegionUnion[d1, d2, d3, d4],
RegionIntersection[d1, d2, d3, d4]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a56/a561688e-516a-40db-bbe9-6ae8b61e4807/067c3870f167742f.png) |
| Out[9]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License