Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SymbolicSystem

Source Notebook

Get the evolution of a symbolic system

Contributed by: Abigail Nussey

ResourceFunction["SymbolicSystem"][rule,init,t]

generates a list representing the evolution of the symbolic system with the specified rule from initial condition init for t steps.

Details and Options

Some interesting rules are:
e[x_][y_]→x[y][e[y]]
e[x_][y_]→x[x[y]]
e[x_][y_]→e[x][y]
e[x_][y_]→x[e[y]][x]
e[x_][y_]→x[y[x]]
e[x_][y_]→x[y[e][e]]
e[x_][y_]→e[x[e][y[e]]]
e[x_][y_]→e[y[e[e][e]][x]]

Examples

Basic Examples (2) 

Sample evolution of a symbolic system:

In[1]:=
ResourceFunction["SymbolicSystem"][{e[x_][y_] -> x[e[y]][x]}, e[e[e][e]][e][e], 5] // Column
Out[1]=

Define the auxiliary function ToBrackets:

In[2]:=
ToBrackets[rule_, init_, steps_] := Module[{e }, StringSplit[ StringReplace[ToString[#1], "e" -> ""], ""] & /@ (ResourceFunction["SymbolicSystem"][rule, init, steps] )];
In[3]:=
ToBrackets[e[x_][y_] -> x[e[y]][x], e[e[e][e]][e][e], 5] // Column
Out[3]=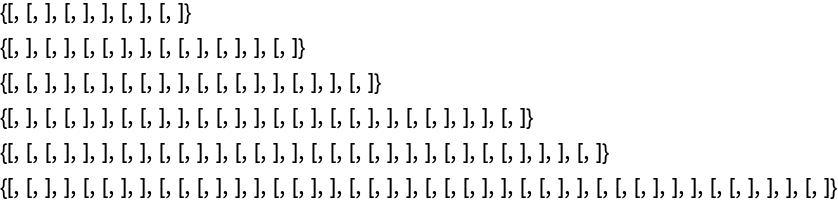

Steps versus step lengths:

In[4]:=
ListLinePlot[ Length /@ ToBrackets[e[x_][y_] -> x[e[y]][x], e[e[e][e]][e][e], 37], Filling -> Axis, AspectRatio -> 1/4]
Out[4]=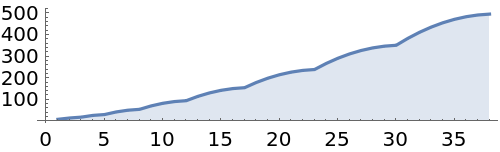

Plot the evolution of the symbolic system:

In[5]:=
Module[{evolved = ToBrackets[e[x_][y_] -> x[e[y]][x], e[e[e][e]][e][e], 5]}, Graphics[ Flatten[Table[{Black, EdgeForm[Thin], evolved[[j]][[i]] /. {"]" -> White, "[" -> RGBColor[ 0.22222222222222227`, 0.22222222222222227`, 0.22222222222222227`]}, Rectangle[{i - 1, 1 - j}, {i, 2 - j}], evolved[[j]][[ i]] /. {"]" -> RGBColor[ 0.33333333333333337`, 0.33333333333333337`, 0.33333333333333337`], "[" -> GrayLevel[0.85]}, Text[Style[evolved[[j]][[i]], FontSize -> 8], {1/2 (2 i - 1), 1/2 (3 - 2 j)}]}, {j, Length[evolved]}, {i, Length[evolved[[j]]]}]]]]
Out[5]=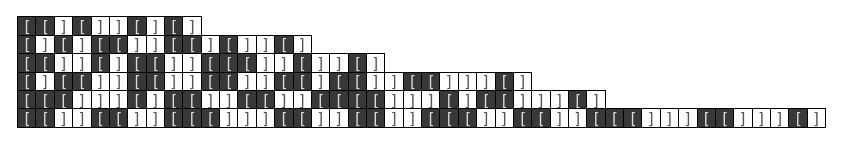
In[6]:=
Module[{evolved = ToBrackets[e[x_][y_] -> x[e[y]][x], e[e[e][e]][e][e], 37]}, ArrayPlot[evolved /. {"]" -> 0, "[" -> 1}, PixelConstrained -> 5, ColorRules -> {0 -> LightGray, 1 -> Black}, Frame -> False]]
Out[6]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 19 February 2019

Source Metadata

  • Citation:
    • Stephen Wolfram (2002), A New Kind of Science

License Information