Function Repository Resource:

SymbolicIndexedArray

Source Notebook

Create a symbolic indexed array

Contributed by: Peter Burbery

ResourceFunction["SymbolicIndexedArray"][symbol, dims]

creates a symbolic array by indexing symbol with subscripts indicating its position in an array with dimensions dims.

Details

ResourceFunction["SymbolicIndexedArray"] can be used to generate vectors, matrices, tensors, arrays, row vectors, column vectors, block matrices, tensors, 4-vectors, arrays, lists, and tuples.

The default format function is Indexed. The format function can be specified with “Subscript” for Subscript or “Indexed” for Indexed as a third argument.

Examples

Basic Examples (1)

Create a 3 by 3 matrix:

In[1]:=

Out[1]=

Scope (2)

Display the matrix in different forms:

In[2]:=

Column@Normal@
AssociationMap[#[
ResourceFunction["SymbolicIndexedArray"][
x, {3, 3}]] &, {Identity, MatrixForm, TableForm, Grid}]

Out[2]=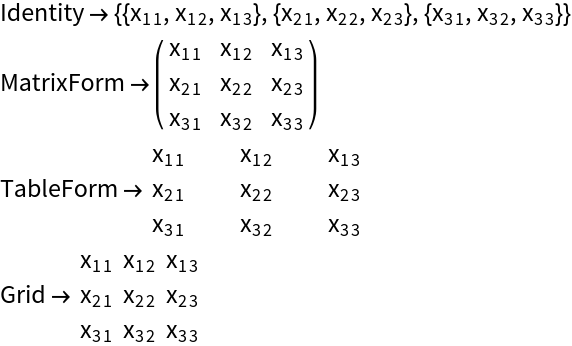

Create a tensor with subscripts:

In[3]:=

Column@Normal@
AssociationMap[#[
ResourceFunction["SymbolicIndexedArray"][x, {4, 4}, "Subscript"]] &, {Identity, MatrixForm, TableForm, Grid}]

Out[3]=

Applications (9)

Add symbolic vectors:

In[4]:=

Out[4]=

Perform additional vector computations::

In[5]:=

Out[5]=

In[6]:=

Out[6]=

In[7]:=

Out[7]=

In[8]:=

Out[8]=

In[9]:=

Out[9]=

In[10]:=

Out[10]=

In[11]:=

Out[11]=

In[12]:=

Out[12]=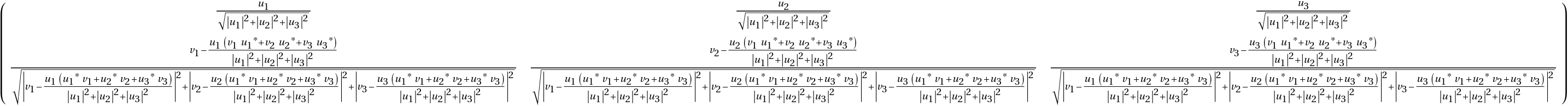

Norm with various vector norms:

In[13]:=

Out[13]=

In[14]:=

Out[14]=

In[15]:=

$Norm[ResourceFunction["SymbolicIndexedArray"][u, 3], \[Infinity]]$

Out[15]=

Upper triangularize a matrix:

In[16]:=

Out[16]=

Lower triangularize a matrix:

In[17]:=

$LowerTriangularize[ ResourceFunction[ "SymbolicIndexedArray"][\[ScriptL], {3, 3}]] // MatrixForm$

Out[17]=

Find elements on the main diagonal:

In[18]:=

$Diagonal[ ResourceFunction["SymbolicIndexedArray"][\[ScriptCapitalD], {3, 3}]]$

Out[18]=

Find elements on the superdiagonal:

In[19]:=

$Diagonal[ ResourceFunction["SymbolicIndexedArray"][\[ScriptCapitalD], {3, 3}], 1]$

Out[19]=

Find elements on the subdiagonal:

In[20]:=

$Diagonal[ ResourceFunction[ "SymbolicIndexedArray"][\[ScriptCapitalD], {3, 3}], -1]$

Out[20]=

Perform a Dot product on symbolic matrices:

In[21]:=

Out[21]=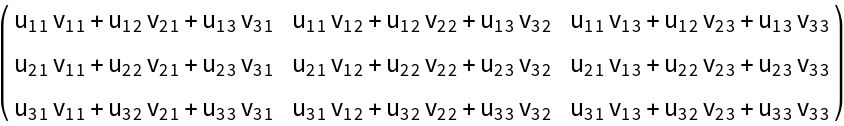

Perform various other matrix operations:

In[22]:=

Out[22]=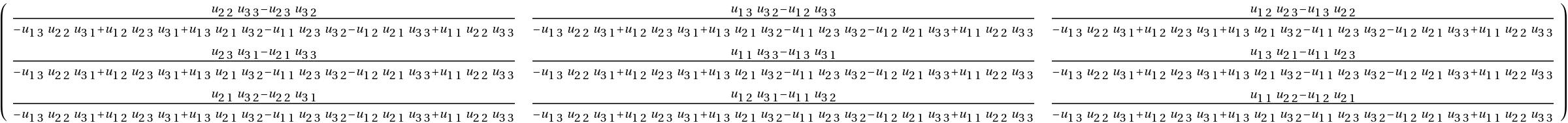

In[23]:=

Out[23]=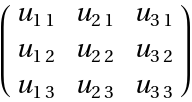

In[24]:=

Out[24]=

In[25]:=

Out[25]=

In[26]:=

Out[26]=

In[27]:=

Out[27]=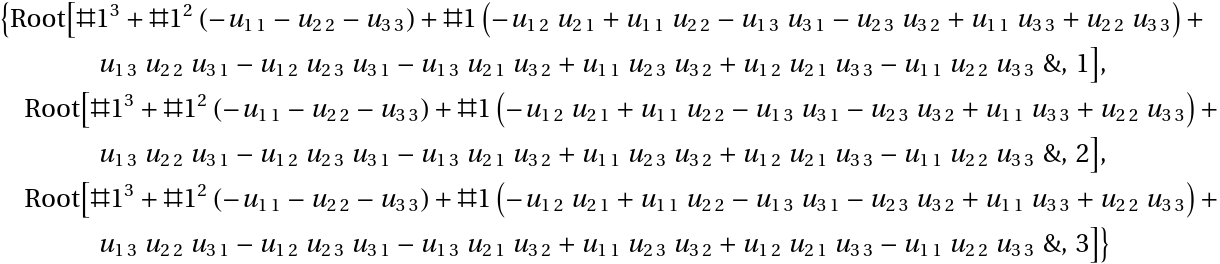

Publisher

Version History

1.0.0 – 16 August 2022

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License