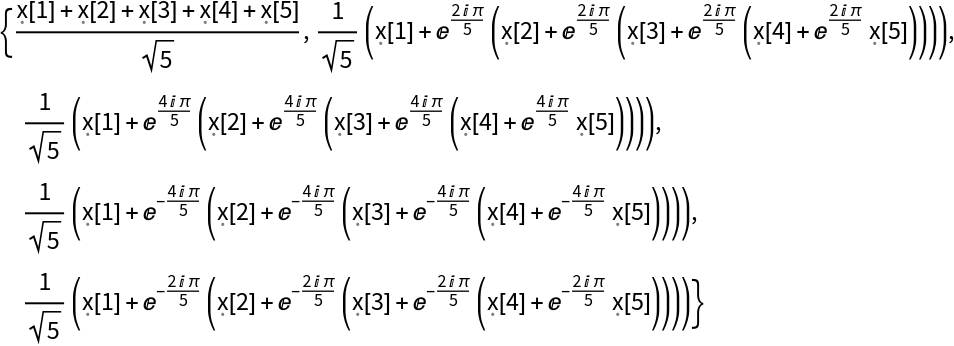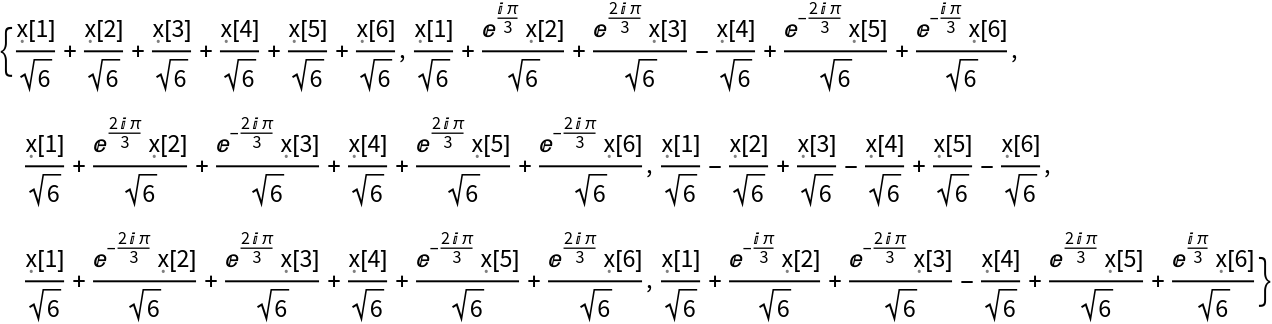Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SymbolicFourier (1.0.0) current version: 1.1.0 »

Source Notebook

A symbolic version of the Fourier function

Contributed by: Jan Mangaldan

ResourceFunction["SymbolicFourier"][list]

finds the discrete Fourier transform of a list of complex numbers.

Details and Options

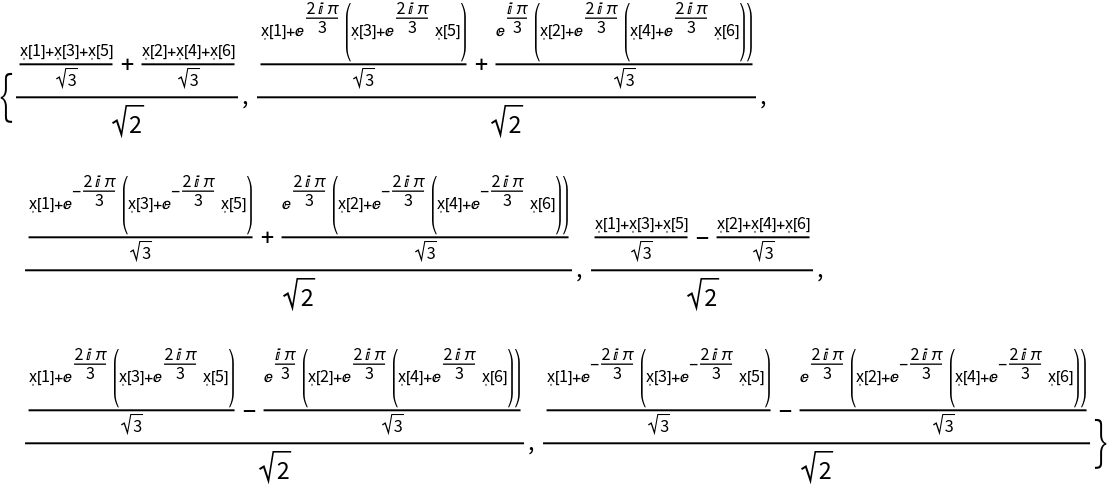
The discrete Fourier transform vs of a list ur of length n is by default defined to be .
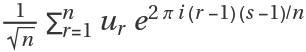
As with the numeric Fourier function, the zero frequency term appears at position 1 in the resulting list.
Other definitions are used in some scientific and technical fields.
Different choices of definitions can be specified using the option FourierParameters.
With the setting FourierParameters→{a,b}, the discrete Fourier transform computed by Fourier is .
Some common choices for {a,b} are {0,1} (default), {-1,1} (data analysis) and {1,-1} (signal processing).
The setting b=-1 effectively corresponds to conjugating both input and output lists.
To ensure a unique inverse discrete Fourier transform, |b| must be relatively prime to n.
The list of data supplied to ResourceFunction["SymbolicFourier"] need not have a length equal to a power of two.
The list given in ResourceFunction["SymbolicFourier"][list] must be a vector, but does not need to have numeric entries.

Examples

Basic Examples (2) 

Find a discrete Fourier transform:

In[1]:=
ResourceFunction["SymbolicFourier"][{1, 1, 2, 2, 1, 1, 0, 0}]
Out[1]=

Compare with the built-in Fourier:

In[2]:=
{N[%], Fourier[N[{1, 1, 2, 2, 1, 1, 0, 0}]]} // Chop
Out[2]=

Scope (1) 

SymbolicFourier can be used on lists with symbolic elements:

In[3]:=
ResourceFunction["SymbolicFourier"][Array[\[FormalX], 5]]
Out[3]=

Options (1) 

FourierParameters (1) 

Use FourierParameters to specify a different normalization:

In[4]:=
ResourceFunction["SymbolicFourier"][Array[\[FormalX], 5], FourierParameters -> {1, -1}]
Out[4]=

Properties and Relations (2) 

Applying SymbolicFourier to a List is the same as pre-multiplying it with FourierMatrix:

In[5]:=
r1 = ResourceFunction["SymbolicFourier"][Array[\[FormalX], 6]]
Out[5]=
In[6]:=
r2 = FourierMatrix[6] . Array[\[FormalX], 6]
Out[6]=
In[7]:=
r1 == r2 // FullSimplify
Out[7]=

The result of SymbolicFourier produces a result in factored form, often with a lower LeafCount:

In[8]:=
{LeafCount[r1], LeafCount[r2]}
Out[8]=

Possible Issues (1) 

SymbolicFourier currently does not support lists with depth greater than 1:

In[9]:=
ResourceFunction["SymbolicFourier"][{{a, b}, {c, d}}]
Out[9]=

Version History

  • 1.1.0 – 06 March 2023
  • 1.0.0 – 26 May 2021

Source Metadata

  • Citation:
    • de Boor, C., "FFT as Nested Multiplication, with a Twist." SIAM Journal on Scientific and Statistical Computing, vol. 1, no. 1, 173–178, 1980. DOI: 10.1137/0901009
    • Glassman J.A., "A Generalization of the Fast Fourier Transform." IEEE Transactions on Computers, vol. C-19, no. 2, 105–116, 1970. DOI: 10.1109/T-C.1970.222875

Related Resources

Author Notes

Support for matrix/tensor arguments will be added at a later date.

License Information