Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SwapOrderedPermutations

Source Notebook

Construct a list of permutations so that successive permutations differ by exactly one transposition

Contributed by: Wolfram Staff (original content by Sriram V. Pemmaraju and Steven S. Skiena)

ResourceFunction["SwapOrderedPermutations"][l]

constructs all permutations of list l such that adjacent permutations differ by only one transposition.

Details and Options

A transposition is a swap of two elements of an ordered list with all others staying at the their respective positions.
ResourceFunction["SwapOrderedPermutations"] uses Heap’s algorithm.

Examples

Basic Examples (2) 

Compute a full list of permutations each differing from the previous permutation by exactly one transposition:

In[1]:=
ResourceFunction["SwapOrderedPermutations"][{a, b, c}]
Out[1]=

Find swap-ordered permutations for four elements:

In[2]:=
ResourceFunction["SwapOrderedPermutations"][Range[4]]
Out[2]=

Properties and Relations (2) 

SwapOrderedPermutations differs from Permutations in the ordering of the result:

In[3]:=
Permutations[{1, 2, 3, 4}]
Out[3]=
In[4]:=
ResourceFunction["SwapOrderedPermutations"][{1, 2, 3, 4}]
Out[4]=
In[5]:=
Sort[%] === %%
Out[5]=

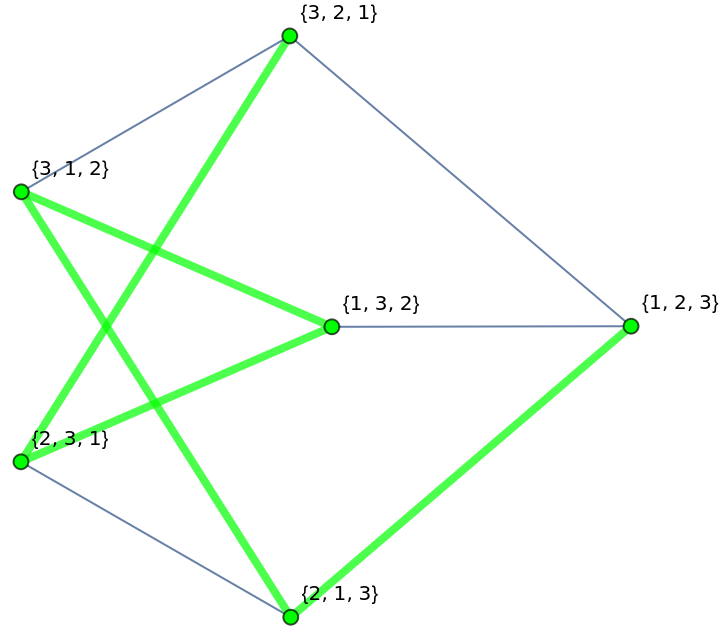
SwapOrderedPermutations defines a Hamiltonian path in the transposition graph:

In[6]:=
PermutationTranspositionQ[l1_, l2_] := Module[{nz = Select[l1 - l2, (# =!= 0) &]}, Length[nz] == 2 && nz[[1]] == -nz[[2]]]; HighlightGraph[ RelationGraph[PermutationTranspositionQ, Permutations[Range[3]], VertexLabels -> "Name"], Style[PathGraph[ ResourceFunction["SwapOrderedPermutations"][ Range[3]]], {AbsoluteThickness[4], Green}]]
Out[6]=

Version History

  • 1.0.0 – 27 August 2020

Related Resources

License Information