Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Sumset

Source Notebook

Sumset gives the sumset of a collection of sets or the h-fold sumset of a set

Contributed by: Kevin O'Bryant
Professor of Mathematics
City University of New York
(College of Staten Island, The Graduate Center)

ResourceFunction["Sumset"][A1,A2,…]

gives the sorted set of sums a1+a2+⋯ (with repetitions removed) where ai∈Ai.

ResourceFunction["Sumset"][h,A]

gives the sorted set of sums a1+a2+⋯+ah (with repetitions removed) where ai∈A.

Details

ResourceFunction["Sumset"] gives all possible sums from taking one element in each of the given sets.
The sumset is also called the Minkowski sum in some analytic settings.
Uses Union, Flatten and Outer, so may not work as expected if some of the elements being added are themselves lists.
Computes ResourceFunction["Sumset"][2k,A] for enough values of k to compute ResourceFunction["Sumset"][h,A], simplifying along the way, so this is faster than naive implementations. (This is akin to using a power tree method to compute a power.)

Examples

Basic Examples (3) 

Compute the 6-fold sumset of a set of integers:

In[1]:=
ResourceFunction["Sumset"][6, {0, 1, 2, 3, 4, 5, 50}]
Out[1]=

Compute the sumset of points in the plane:

In[2]:=
setofpoints = {{0, 0}, {0, 1}, {0, 3}, {1, 4}}; ResourceFunction["Sumset"][2, setofpoints]
Out[3]=

Compute the sumset of points in 3-space:

In[4]:=
setofpoints = {{0, 0, 0}, {0, 1, 1}, {0, 3, -1}, {1, 4, 2}}; set2ofpoints = {{0, -1, -1}, {1, 1, 1}, {2, 2, 2}, {3, 3, 10}}; ResourceFunction["Sumset"][setofpoints, set2ofpoints]
Out[6]=

Neat Examples (2) 

The expected size of Complement[Range[2,n],Sumset[2,A]] is just under 10, if A is a random subset of Range[1,n] (reference is Many Sets have More Sums than Differences, G. Martin and K. O'Bryant, Additive combinatorics, 287--305, CRM Proc. Lecture Notes, 43, Amer. Math. Soc., Providence, RI, 2007):

In[7]:=
n = 100; data = Table[ 2 n - 1 - Length[ResourceFunction["Sumset"][2, RandomSample[Range[1, n], n/2]]], {1000}]; Histogram[data, {1}, PlotLabel -> "mean = " <> ToString[Mean[N[data, 2]]]]
Out[9]=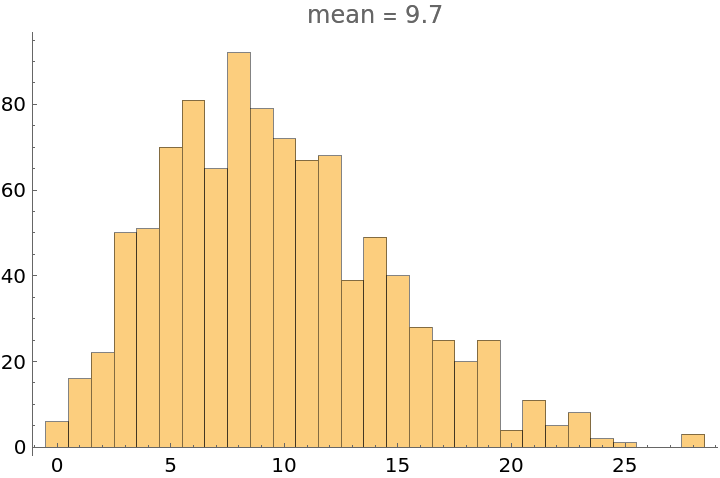

As h grows, Sumset[h,A] grows to contain the interior of a polygon (scaled to h):

In[10]:=
domain = Flatten[Table[{i, j}, {i, -4, 4}, {j, -4, 4}], 1]; A = RandomSample[domain, 10]; Manipulate[ ListPlot[ResourceFunction["Sumset"][h, A], AspectRatio -> 1, ImageSize -> Small, PlotRange -> (4 h + 1) {{-1, 1}, {-1, 1}}, Ticks -> {Range[-4 h, 4 h, h], Range[-4 h, 4 h, h]}], {h, 1, 24, 1}, SaveDefinitions -> True]
Out[11]=

Publisher

Kevin O'Bryant

Requirements

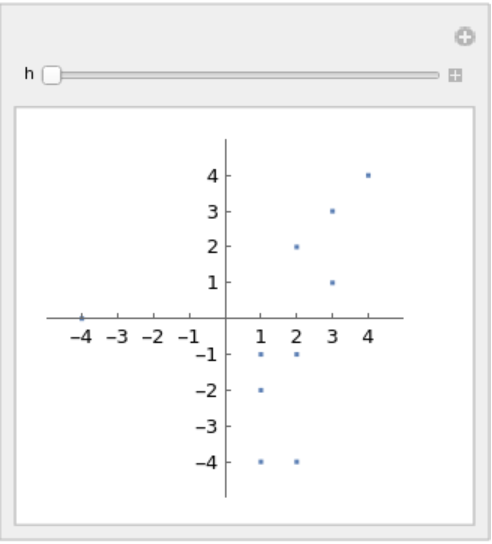Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 03 June 2024

Source Metadata

  • Citation:
    • Elementary Methods in Number Theory, Melvyn B. Nathanson, Springer, 2000. (Chapter 4)

Author Notes

This is an inefficient approach to computing the table Table[Sumset[h,A],{h,1,32}], as the function "sums[k]" inside Sumset gets recomputed every time at great expense. If A is a set of integers, the code is still fast enough, but if A is a set of points, it is prohibitive.

License Information