Function Repository Resource:

SumRule

See how to apply the sum rule for derivatives

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["SumRule"][f,x]

applies the sum rule for computing the derivative of f with respect to x, returning an inactive result.

Details

The sum rule for derivatives states that the derivative of a sum of terms is equal to the sum of the derivatives of each term.

SumRule accepts the following options:

"PrintRule"

False

print a statement of the sum rule and the derivative rules relevant to each term of the given sum

"PrintNapkin"

False

print the side "napkin" work needed for computing components of the sum rule

“InactiveInnerDerivatives"

False

keep the derivatives of the components inactivated

Examples

Basic Examples (1)

See how to apply the sum rule to compute the derivative of sin(x)+ x² with respect to x:

In[1]:=

Out[1]=

Scope (1)

If there is no explicit sum in the first argument of SumRule, one of the terms is taken to be 0:

In[2]:=

Out[2]=

Options (3)

InactiveInnerDerivatives (1)

Setting "InactiveInnerDerivatives" to True inactivates the derivatives of the factors within the structure of the sum rule:

In[3]:=

Out[3]=

PrintNapkin (1)

Setting "PrintNapkin" to True prints a grid with the side "napkin" work needed to apply the sum rule (i.e., identifying and computing the derivatives of each term):

In[4]:=

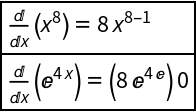
Out[4]=

PrintRule (1)

Setting "PrintRule" to True prints a general statement of the sum rule for derivatives along with general statements of the derivative rule needed to compute the derivative of each term:

In[5]:=