Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get a list of subsets of a list along with their complements
ResourceFunction["SubsetsWithComplements"][list] gives a List of all possible subsets of list along with their complements. | |
ResourceFunction["SubsetsWithComplements"][list,n] gives all subsets containing at most n elements along with their corresponding complements. | |
ResourceFunction["SubsetsWithComplements"][list,{n}] gives all subsets containing exactly n elements. | |
ResourceFunction["SubsetsWithComplements"][list,{nmin,nmax}] gives all subsets containing between nmin and nmax elements. | |
ResourceFunction["SubsetsWithComplements"][list,nspec,s] limits the result to the first s subsets. | |
ResourceFunction["SubsetsWithComplements"][list,nspec,{s}] gives, if possible, the sth subset and complement. |
Get all the subsets of a List of characters, paired with their complements:
| In[1]:= |
| Out[1]= | 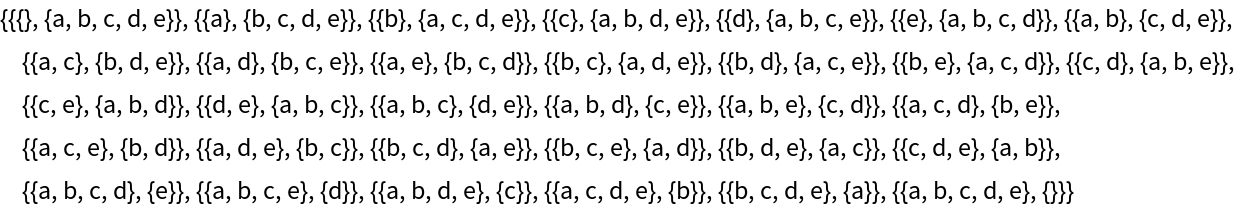 |
Take a List of three characters and get all the one-element subsets thereof and their complements:
| In[2]:= |
| Out[2]= |
Get all subsets from a List of five characters with at most two elements, along with their complements:
| In[3]:= |
| Out[3]= |  |
Take a List of five characters and get all subsets with between two and three elements and their complements:
| In[4]:= |
| Out[4]= | 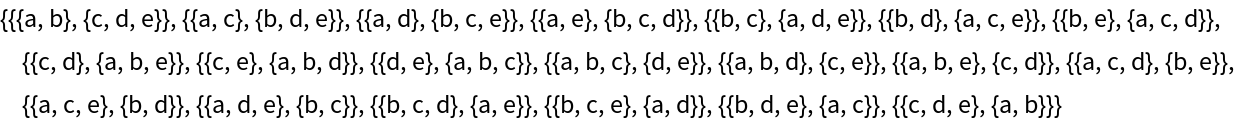 |
Get the first three two-element subsets and complements from a list with six elements:
| In[5]:= |
| Out[5]= |  |
Get the seventh two-element subset and complements of a list with six elements:
| In[6]:= |
| Out[6]= |
Find and show conditions under which each expression in a List will have a value greater than that of any other expression in the list:
| In[7]:= |
| In[8]:= |
| Out[8]= |
| In[9]:= |
| In[10]:= |
| Out[10]= | 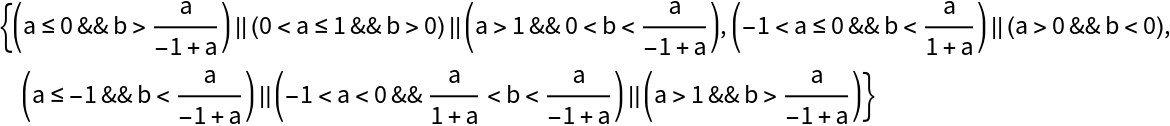 |
| In[11]:= |
| Out[11]= | 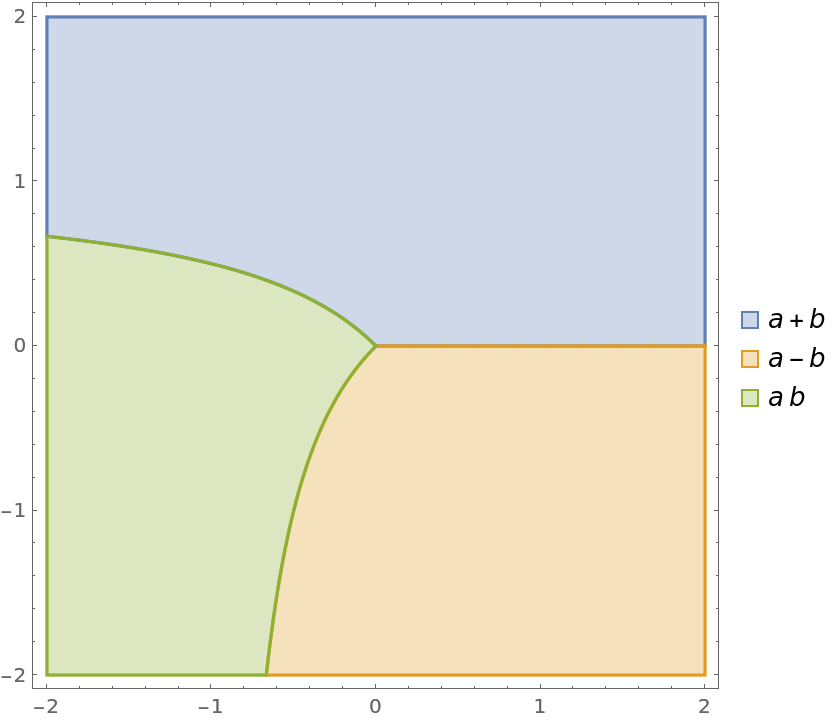 |
Do similarly for the lowest value of any expression in the List:
| In[12]:= |
| In[13]:= |
| Out[13]= | 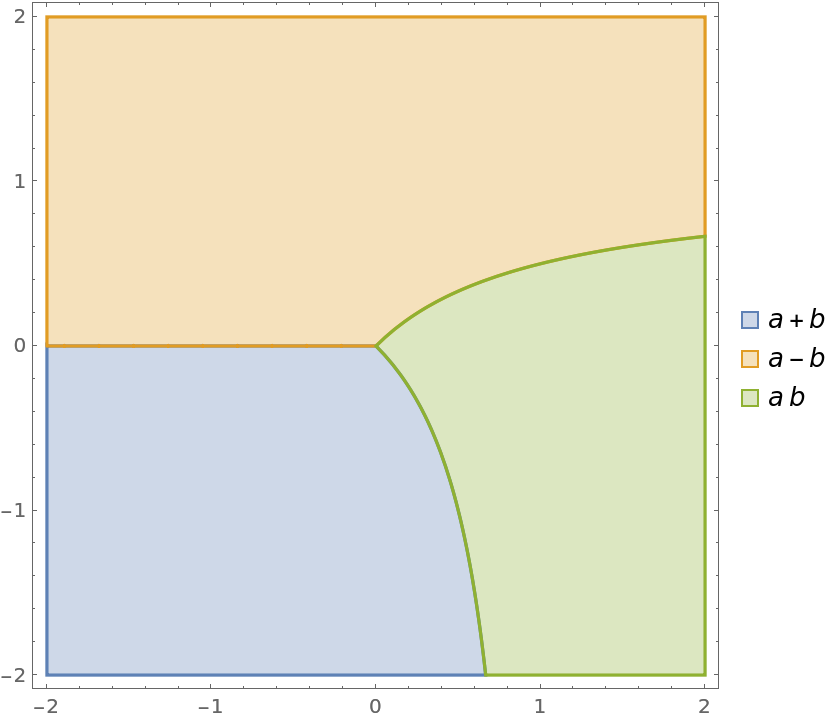 |
A certain classifier predicts the probabilities that a person will be in each of three possible classes. A misclassification results in a utility of –1, except when a person is really in the first class but is misclassified as being a member of the second class. This latter case results in a utility of –u, where u is some non-negative number. For each value of u, find and show the set of classifier probabilities {p1,(1–p1)p2,1–(p1+(1–p1)p2)} that result in each prediction being the one that maximizes expected utility:
| In[14]:= |
| Out[14]= |
| In[15]:= | ![bestClassificationFunction = Function[u, Evaluate@Function[{p1, p2, p3}, Evaluate[
Query[Simplify, MapAt[First, {1}]/*Apply[Greater]/*Thread/*
Apply[And]/*(Reduce[
And[#, Total[{p1, p2, p3}] == 1, And @@ Map[NonNegative, {p1, p2, p3}]], {p1, p2, p3}] &)][
ResourceFunction["SubsetsWithComplements"][
expectedUtilities, {1}]]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/485/485d0f21-baa3-4e41-ba89-dbd24fcc8118/0bddbbacb59fd3d2.png) |
| Out[15]= | 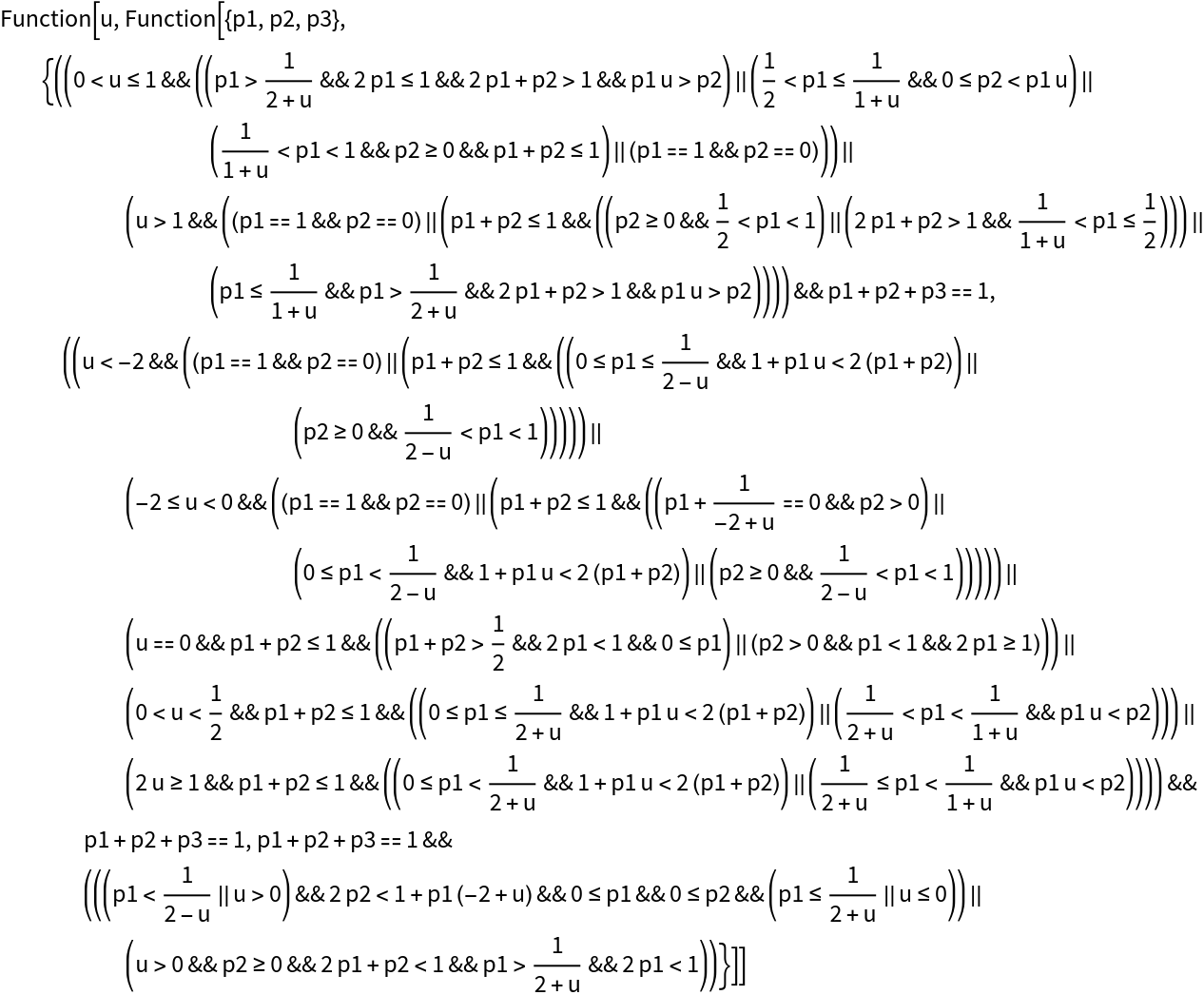 |
| In[16]:= | ![RegionPlot3D[{bestClassificationFunction[u][p1, p2 (1 - p1), 1 - (p1 + p2 (1 - p1))][[1]], bestClassificationFunction[u][p1, p2 (1 - p1), 1 - (p1 + p2 (1 - p1))][[2]], bestClassificationFunction[u][p1, p2 (1 - p1), 1 - (p1 + p2 (1 - p1))][[3]]}, {p1, 0, 1}, {p2, 0, 1}, {u, 0.1, 8}, PlotStyle -> Opacity[0.25], Mesh -> None, AxesLabel -> {"p1", "p2", "u"}]](https://www.wolframcloud.com/obj/resourcesystem/images/485/485d0f21-baa3-4e41-ba89-dbd24fcc8118/3535fa7f81099406.png) |
| Out[16]= | 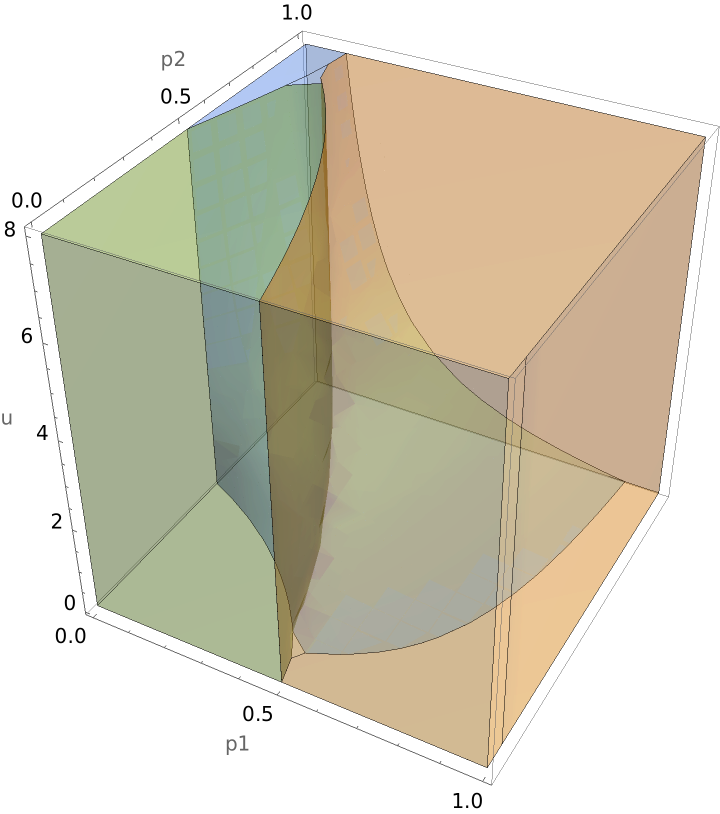 |
This work is licensed under a Creative Commons Attribution 4.0 International License