Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Give the index of a subset
ResourceFunction["SubsetIndex"][list] gives the index of subset list. |
Find the index of a tuple:
| In[1]:= |
| Out[1]= |
The following 3-subset sequence can be extended to infinity:
| In[2]:= |
| Out[2]= |
The function returns indices of one to ten for these subsets:
| In[3]:= |
| Out[3]= |
Any strictly increasing list of nonnegative integers can be considered as a subset with a unique index:
| In[4]:= |
| Out[4]= |
The result above is a subset with a unique index:
| In[5]:= |
| Out[5]= |
Various subsets of differing lengths have index 321:
| In[6]:= |
| Out[6]= |
Some binomial representations of the number 320:
| In[7]:= | ![Column[Row[
Riffle[Table[
TraditionalForm[
Binomial[(ToString /@ #)[[n]], ToString[n]]], {n, 1, Length[#]}], "+"]] & /@ index321, Alignment -> Center]](https://www.wolframcloud.com/obj/resourcesystem/images/330/330861eb-d073-4a99-aaa4-9b815ef192e6/7ecfc25cf82a0da8.png) |
| Out[7]= | 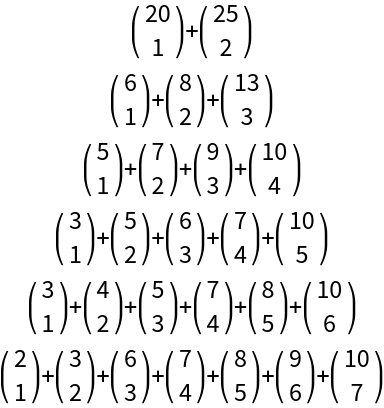 |
Here are some 2-subsets with their indices to show their structure:
| In[8]:= | ![doubles = SortBy[Subsets[Range[0, 5], {2}], Reverse];
Graphics[{Text[
Style[Column[{StringJoin[ToString /@ #], ResourceFunction["SubsetIndex"][#]},
Alignment -> Center], 20], #] & /@ doubles, Blue, Line[doubles]}]](https://www.wolframcloud.com/obj/resourcesystem/images/330/330861eb-d073-4a99-aaa4-9b815ef192e6/56d62b412b7decb0.png) |
| Out[8]= | 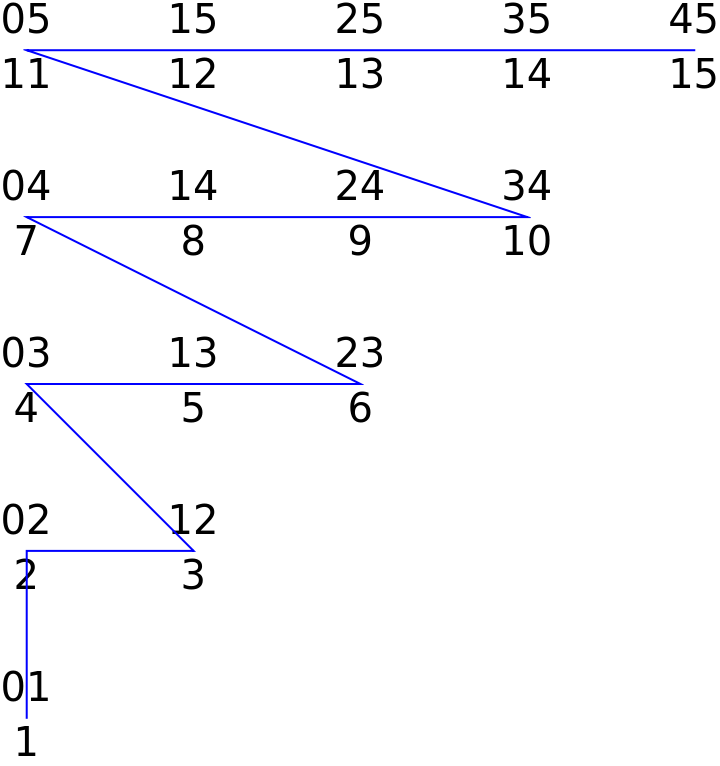 |
The structure of 3-subsets in 3D:
| In[9]:= | ![triples = SortBy[Subsets[Range[0, 5], {3}], Reverse];
Graphics3D[{Text[
Style[Column[{StringJoin[ToString /@ #], ResourceFunction["SubsetIndex"][#]},
Alignment -> Center], 20], #] & /@ triples, Blue, Line[triples]}]](https://www.wolframcloud.com/obj/resourcesystem/images/330/330861eb-d073-4a99-aaa4-9b815ef192e6/1a8c760e5ad56864.png) |
| Out[9]= | 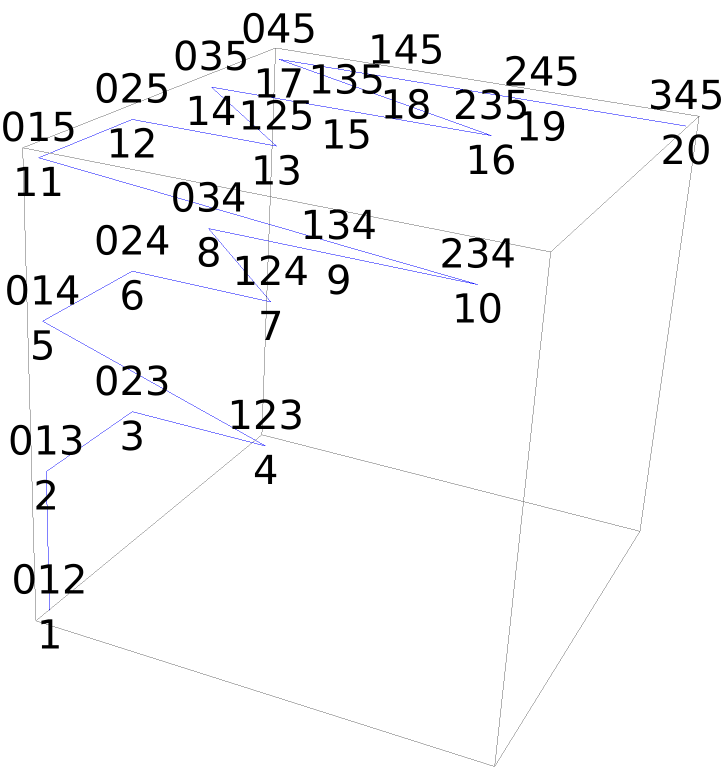 |
Find the index of an eight-term subset:
| In[10]:= |
| Out[10]= |
From that, we get the trillionth number with binary weight eight:
| In[11]:= |
| Out[11]= |
This work is licensed under a Creative Commons Attribution 4.0 International License