Basic Examples (2) 

The permutation group induced on the set of all 2-subsets of {1,2,3} by the cyclic group C₃:

In[1]:=

Out[1]=

In[2]:=

Out[2]=

The permutation group induced on the set of all 2-subsets of {1,2,3,4} by the cyclic group C₄:

In[3]:=

Out[3]=

In[4]:=

Out[4]=

Scope (3) 

Specify the group as a permutation List:

In[5]:=

Out[5]=

Or an abstract group:

In[6]:=

Out[6]=

The permutation group induced on the set of ordered 2-subsets by C₄:

In[7]:=

Out[7]=

In[8]:=

Out[8]=

Applications (3) 

Permutation group on the edges of the 5-vertex wheel graph:

In[9]:=

Out[9]=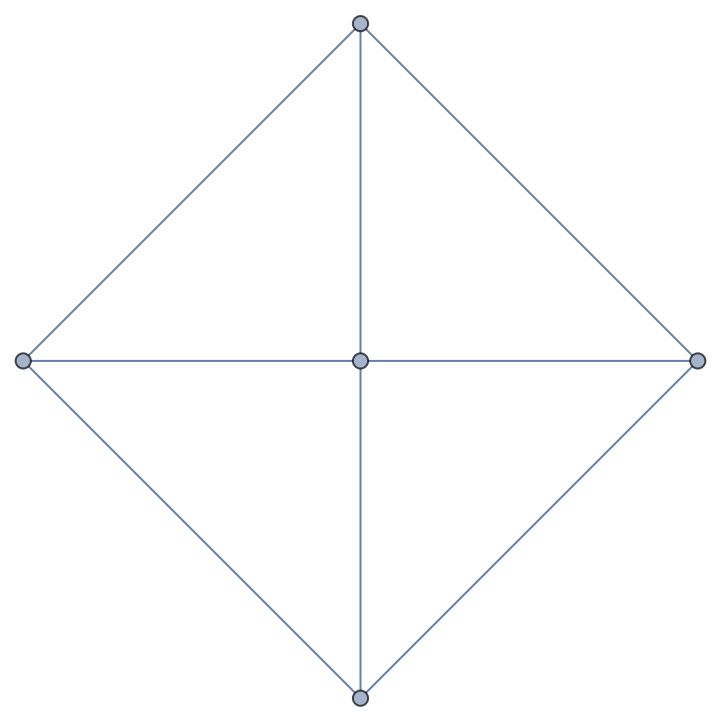

In[10]:=

Out[10]=

The number of colorings of 4-node simple graphs using at most n colors (OEIS A063842):

In[11]:=

Out[11]=

Count the number of distinct dice as orbit representatives of a permutation group induced by a group of symmetries acting on a set of faces of a cube:

In[12]:=

In[13]:=

In[14]:=

In[15]:=

Out[15]=

In[16]:=

Out[16]=

Properties and Relations (2) 

n 2-subsets of {1,2,3,4,5,6} yield a permutation group of n-permutations:

In[17]:=

Out[17]=

In[18]:=

Out[18]=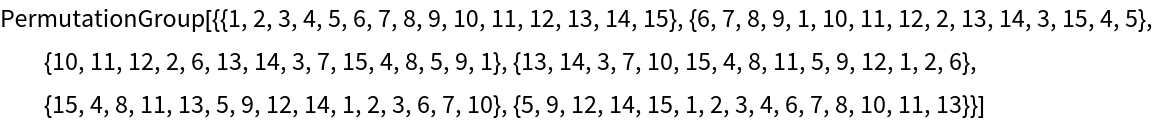

In[19]:=

Out[19]=

The n ordered 2-subsets of {1,2,3,4,5,6} yield a permutation group of n-permutations:

In[20]:=

Out[20]=

In[21]:=

Out[21]=

In[22]:=

Out[22]=