Function Repository Resource:

SubscriptedSymbols

Retrieves all symbols in subscript format from a given expression

Contributed by: E. Chan-López, Víctor Castellanos & Jorge Luis Ramos Castellano

ResourceFunction["SubscriptedSymbols"][expr]

gives all symbols already in subscript format for a given expr.

Details and Options

ResourceFunction["SubscriptedSymbols"] looks for symbols with represents as subscripts anywhere within the expression expr.

ResourceFunction["SubscriptedSymbols"] treats the constant C[i] as symbol in subscript format and retrieves them.

Similar to Variables, ResourceFunction["SubscriptedSymbols"] also has the Modulus option.

Each unique subscript is included in the result only once.

Examples

Basic Examples (3)

Use SubscriptedSymbols with a simple expression:

In[1]:=

Out[1]=

Use SubscriptedSymbols with a list of simple expressions:

In[2]:=

Out[2]=

Use SubscriptedSymbols with a list of expressions that don't contain any symbols in subscript format:

In[3]:=

$ResourceFunction[ "SubscriptedSymbols"] /@ {a*t1, b*x, c*s, d*x1, e*\[Pi]}$

Out[3]=

Scope (8)

Use SubscriptedSymbols with an expression that contains derivatives of any order:

In[4]:=

$ResourceFunction["SubscriptedSymbols"][ Subscript[x, 1]'[t] + Subscript[x, 2]''[t] + \!$\*SuperscriptBox[ SubscriptBox[\(x$, $3$], TagBox[ RowBox[{"(", RowBox[{"1", ",", "1"}], ")"}], Derivative], MultilineFunction->None]\)[t, s]]$

Out[4]=

Use SubscriptedSymbols with a list of simple expressions:

In[5]:=

Out[5]=

Use SubscriptedSymbols with a list of more complicated expressions:

In[6]:=

$ResourceFunction[ "SubscriptedSymbols"]@{(Subscript[x, 1]^(1 + n) + Subscript[x, 2]) (Subscript[x, 3]^(-2 + m) - x4), Sqrt[ Subscript[\[Alpha], \[Beta]][t] + Subscript[\[Theta], \[Psi]][t]], Power[(Subscript[x, 4][t, s] + 2 Subscript[w, 3][t, s])^3, (5)^-1]}$

Out[6]=

Use SubscriptedSymbols with a non-linear system of differential equations:

In[7]:=

$ResourceFunction[ "SubscriptedSymbols"][{Subscript[x, 1]'[t] == -Subscript[x, 1][t]^2 - Subscript[x, 2][t], Subscript[x, 2]'[t] == 2 Subscript[x, 1][t] - Subscript[x, 2][t]^3}]$

Out[7]=

Use SubscriptedSymbols with a hyperbolic partial differential equation with non-rational coefficients:

In[8]:=

$ResourceFunction["SubscriptedSymbols"][ D[Subscript[u, 1][x, y], {x, 2}] - 2 Sin[x] D[Subscript[u, 1][x, y], x, y] - Cos[x]^2 D[Subscript[u, 1][x, y], {y, 2}] - Cos[x] D[Subscript[u, 1][x, y], y] == 0]$

Out[8]=

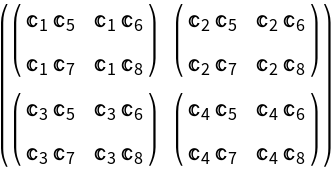
Use SubscriptedSymbols with a tensor product of matrices involving C[i]:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

Use SubscriptedSymbols with a univariate polynomial:

In[11]:=

Out[11]=

Use SubscriptedSymbols with a polynomial in two variables:

In[12]:=

Out[12]=

Options (2)

Modulus (2)

Find subscripted symbols present after reducing coefficients modulo 2:

In[13]:=

Out[13]=

For polynomials, SubscriptedSymbols and Variables gives the same results:

In[14]:=

Out[14]=

Applications (5)

Use SubscriptedSymbols to define a simple function that transforms symbols, already in subscript format, into symbols that can be converted to subscript format within a given expression:

In[15]:=

$ToSymbolFormat[expr_] /; SameQ[Head[expr], Subscript] := ToExpression[StringJoin@(ToString /@ Level[expr, {-1}])] ToSymbolFormat[expr_] /; SameQ[Head[expr], C] := expr /. C[s_Integer?NonNegative] :> ToExpression[ToString[C] <> ToString[s]] ToSymbolFormat[expr_] := expr /. Thread[ ResourceFunction["SubscriptedSymbols"][expr] -> ToSymbolFormat /@ ResourceFunction["SubscriptedSymbols"][expr]]$

Use ToSymbolFormat with a tensor of rank 3:

In[16]:=

$MatrixForm@ ToSymbolFormat@ D[{Subscript[x, 1]^2 Subscript[y, 1] + Subscript[x, 1], -Subscript[y, 1] Subscript[x, 1]^3 - 2 Subscript[x, 1]}, {{Subscript[x, 1], Subscript[y, 1]}, 2}]$

Out[16]=

Use ToSymbolFormat with a polynomial in two variables:

In[17]:=

Out[17]=

Use ToSymbolFormat with a function:

In[18]:=

$ToSymbolFormat[Function[{x, y}, C[1]*E^(-x^2 - y^2) + C[2]]]$

Out[18]=

Use ToSymbolFormat with an expression involving nested subscripts:

In[19]:=

$ToSymbolFormat[ Cos[Subscript[x, Subscript[\[Alpha], \[Beta]]]] + Sin[Subscript[x, Subscript[\[Psi], \[CurlyPhi]]]]]$

Out[19]=

Properties and Relations (3)

Unlike Variables, SubscriptedSymbols looks for subscripted variables in non-polynomial expressions:

In[20]:=

Out[20]=

Use SubscriptedSymbols with a list of functions:

In[21]:=

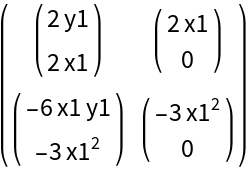
$ResourceFunction[ "SubscriptedSymbols"] /@ {Function[{x, y}, C[1]*E^(-x^2 - y^2) + C[2]], Function[{x, t}, C[3] + x^2/6 + C[4][t - 1/6 (1 + Sqrt[13]) x]]}$