Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Construct special triangles of a triangle
ResourceFunction["SubTriangle"][tri, special] returns the triangle identified by special fom the triangle tri. |
| AAOA | anti-altimedial orthic axes triangle. Ref: X15015 |
| Anticomplementary | triangle with ABC as medial triangle. |
| BCI | centers of three tangent circles of equal size. |
| Brocard1 | coincident points for lines through Brocard points. |
| Brocard2 | see references. |
| Brocard3 | isogonal conjugate of "Brocard1". |
| Circummedial | circumcevian triangle of the centroid. |
| CircumcircleMidArc | mid-arc points of the circumcircle. |
| Circumorthic | circumcevian triangle of the orthocenter. |
| Contact | tangency points of incircle. |
| Euler1 | midpoints to the orthocenter. |
| EulerGergonneSoddy | right triangle formed by named lines. |
| Excentral | centers of excircles, also called the excenters. |
| Extangents | triangle tangent to the excircles. |
| Extouch1 | tangency points of excircles. |
| Feuerbach | 9-point circle tangency points with excircles. |
| HalfAltitude | midpoints of altitudes. |
| Incentral | cevians of incenter. |
| Intangents | the points of pairwise intersection of the three intangents |
| Kosnita | the circumcenters of the triangles BOC, COA, AOB |
| Malfatti1 | the vertices are the centers of the Malfatti circles |
| Medial | midpoints, or cevians of the centroid. |
| Neuberg1 | centers of Neuberg circles. |
| Neuberg2 | reflections of "Neuberg1". |
| Orthic | cevians of orthocenter. |
| Symmedial | cevians of symmedian point. |
| Tangential | triangle whose incircle is the circumcircle of ABC. |
| Trinh | circumcenter reflection of Kosnita triangle. Ref: X7688 |
Find and show the anticomplementary triangle:
| In[1]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= | 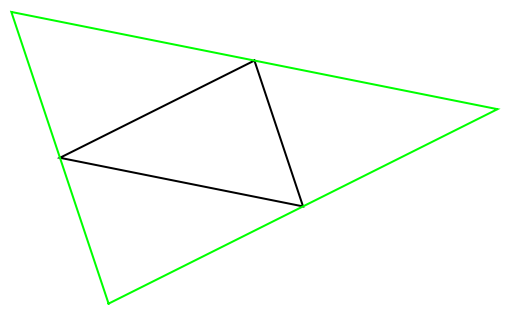 |
Find and show the first Brocard triangle:
| In[4]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= | 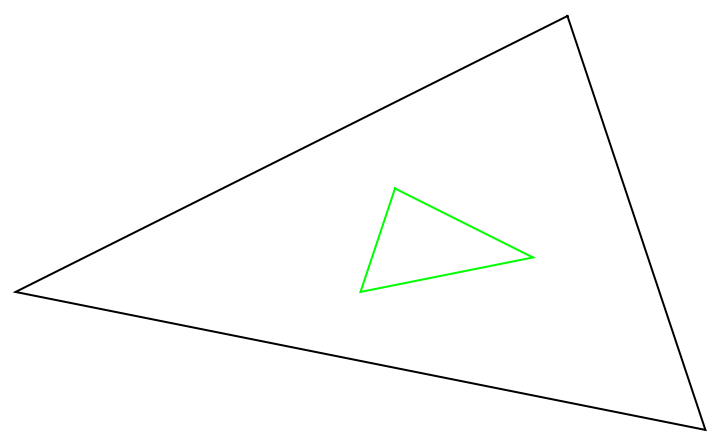 |
Find and show the tangential triangle:
| In[7]:= |
| Out[8]= |
The circumcircle of the triangle is the incircle of the tangential triangle:
| In[9]:= |
| Out[9]= | 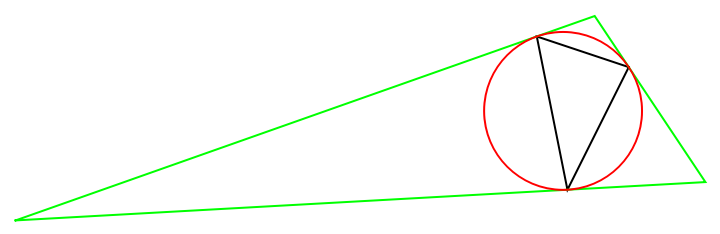 |
Find the half-altitude triangle:
| In[10]:= |
| Out[11]= |
The half-altitude triangle is formed by the midpoints of the altitudes:
| In[12]:= | ![Graphics[{EdgeForm[Black], White, tri, EdgeForm[Green], Opacity[0], half, Red, Opacity[1], Line /@ Transpose[{tri[[1]], ResourceFunction["SubTriangle"][tri, "Orthic"][[1]]}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/cf5/cf5c6518-07e4-434a-872a-9bb8b64ad3c1/1fce6a1df74e1c83.png) |
| Out[12]= | 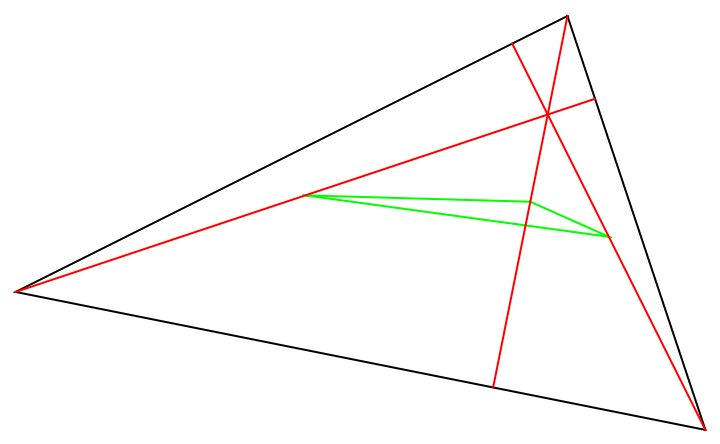 |
Find and show the orthic triangle of the symmedial triangle:
| In[13]:= |
| Out[14]= |
| In[15]:= |
| Out[15]= |
| In[16]:= |
| Out[16]= | 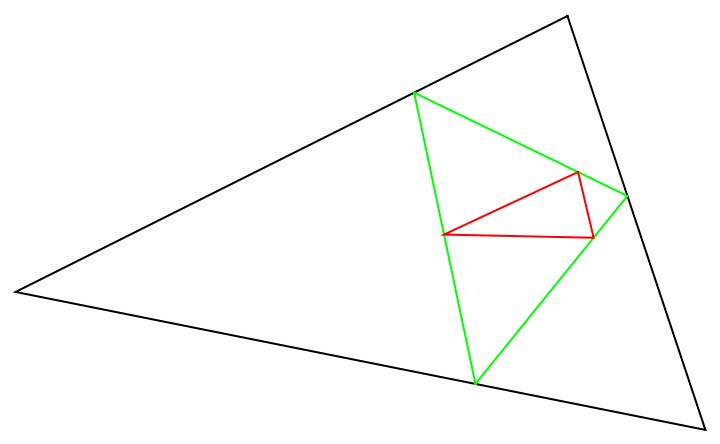 |
Special triangles do not always exist:
| In[17]:= | ![tri = Triangle[CirclePoints[3]];
Graphics[{EdgeForm[Black], White, tri, Opacity[0], Tooltip[{EdgeForm[Hue[RandomReal[{0, 1}]]], ResourceFunction["SubTriangle"][tri, #]}, #] & /@ {"AAOA", "Brocard1", "Brocard2", "Brocard3", "EulerGergonneSoddy"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/cf5/cf5c6518-07e4-434a-872a-9bb8b64ad3c1/57fbd41fdb201680.png) |
| Out[18]= |  |
Show all triangles with Tooltip:
| In[19]:= | ![tri = Triangle[{{2, 1}, {-1, 2}, {2, -3}}];
Graphics[{EdgeForm[Black], White, tri, Opacity[0], Tooltip[{EdgeForm[Hue[RandomReal[{0, 1}]]], ResourceFunction["SubTriangle"][tri, #]}, #] & /@ {"AAOA", "Anticomplementary", "BCI", "Brocard1", "Brocard2", "Brocard3", "Circummedial", "CircumcircleMidArc", "Circumorthic", "Contact", "Euler1", "EulerGergonneSoddy", "Excentral", "Extangents", "Extouch1", "Feuerbach", "HalfAltitude", "Incentral", "Intangents", "Kosnita", "Malfatti1", "Medial", "Neuberg1", "Neuberg2", "Orthic", "Symmedial", "Tangential", "Trinh"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/cf5/cf5c6518-07e4-434a-872a-9bb8b64ad3c1/345db2031f4064e2.png) |
| Out[20]= | 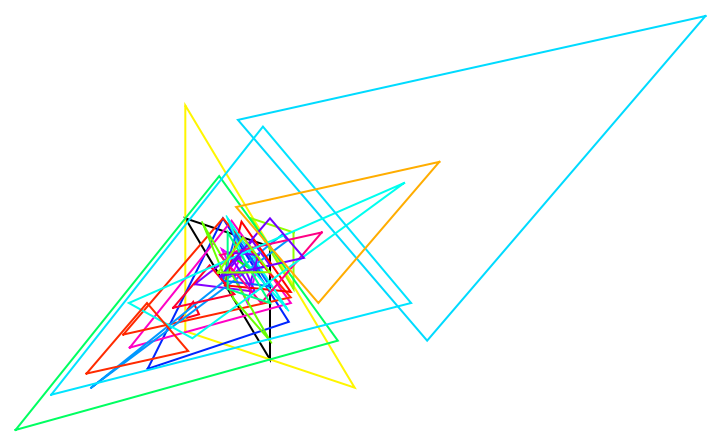 |
Show all triangles in a Manipulate:
| In[21]:= | ![Manipulate[
Graphics[{PointSize[0.03], Blue, Point /@ {AA, BB, CC}, {LightBlue, EdgeForm[{Thick, Blue}], Triangle[{AA, BB, CC}]}, {EdgeForm[Green], Opacity[0], Tooltip[ResourceFunction["SubTriangle"][
Triangle[{AA, BB, CC}], #], #] & /@ {"AAOA", "Anticomplementary", "BCI", "Brocard1", "Brocard2", "Brocard3", "Circummedial", "CircumcircleMidArc", "Circumorthic", "Contact",
"Euler1", "EulerGergonneSoddy", "Excentral", "Extangents", "Extouch1", "Feuerbach", "HalfAltitude", "Incentral", "Intangents", "Kosnita", "Malfatti1", "Medial", "Neuberg1", "Neuberg2", "Orthic", "Symmedial", "Tangential", "Trinh"}}}, ImageSize -> {400, 220}, PlotRange -> {{-5.5, 5.5}, {-3.5, 3.5}}], {{AA, {1.5, 2.5}}, {-5.25, -3.25}, {5.25, 3.25}, Locator, Appearance -> None}, {{BB, {-3.5, -2}}, {-5.25, -3.25}, {5.25, 3.25}, Locator, Appearance -> None},
{{CC, {3., -1.5}}, {-5.25, -3.25}, {5.25, 3.25}, Locator, Appearance -> None}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/cf5/cf5c6518-07e4-434a-872a-9bb8b64ad3c1/54dc05b3fae56b67.png) |
| Out[21]= | 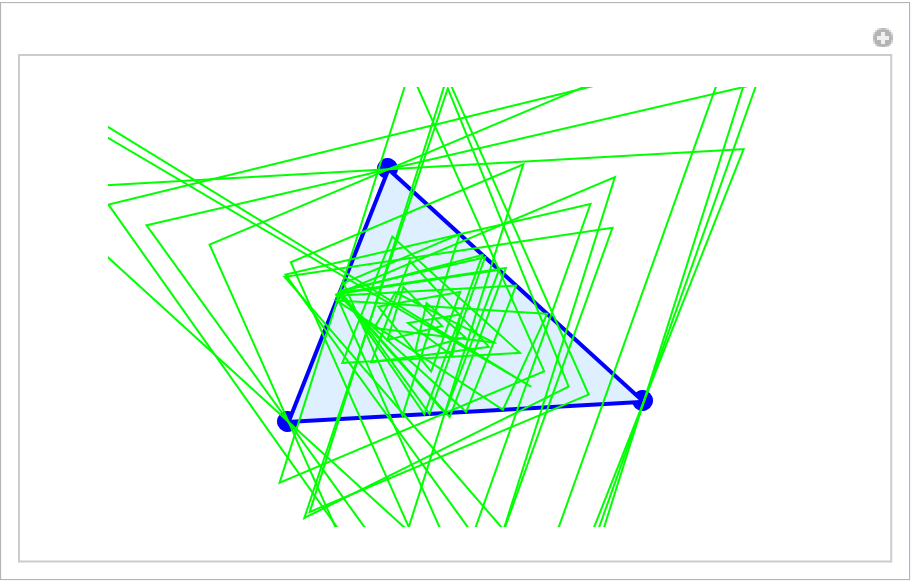 |
Find the Trinh and Kosnita triangles:
| In[22]:= |
| Out[23]= |
The Kosnita and Trinh triangles are symmetric around the circumcenter (in red):
| In[24]:= | ![circ = Circumsphere /@ Subsets[Append[tri[[1]], Circumsphere[tri][[1]]], {3}]; Graphics[{EdgeForm[Black], White, tri, EdgeForm[Green], Opacity[0], trinh, kos, Red, Opacity[1], circ[[1]], Cyan, Drop[circ, 1]}]](https://www.wolframcloud.com/obj/resourcesystem/images/cf5/cf5c6518-07e4-434a-872a-9bb8b64ad3c1/50187cd2e763fe85.png) |
| Out[24]= | 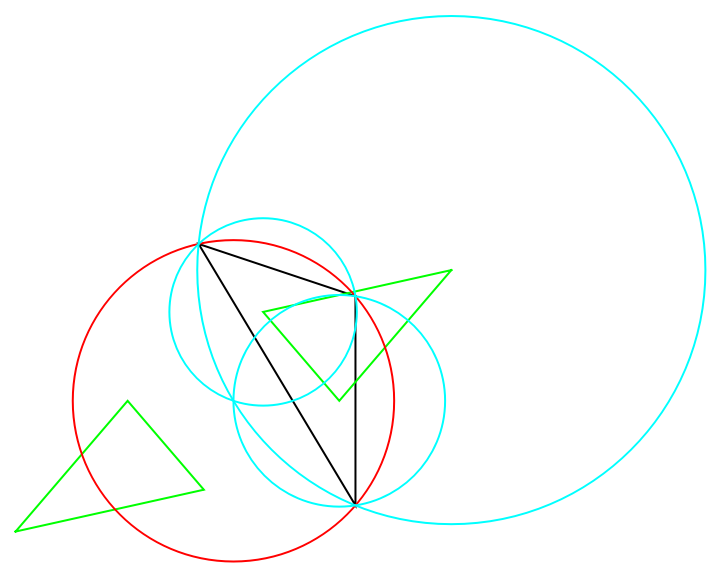 |
This work is licensed under a Creative Commons Attribution 4.0 International License