Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
SubTetrahedron (1.1.0) current version: 1.2.0 »
Construct special tetrahedra of a tetrahedron
Contributed by:
Ed Pegg Jr
ResourceFunction["SubTetrahedron"][tetra, "special"] returns the tetrahedron identified by "special" from the tetrahedron tetra. |
Details
tetra can be a list of vertices or a Tetrahedron object.
For a tetrahedron ABCD, various special tetrahedra are defined:
| "Altitude" | feet of the altitudes |
| "Anticomplementary" | tetrahedron with ABCD as medial tetrahedron |
| "BCI" | centers of four tangent spheres of equal size |
| "Circummedial" | circumcevian tetrahedron of the centroid |
| "Circummonge" | circumcevian tetrahedron of the Monge point |
| "Contact" | tangency points of insphere |
| "Euler" | 2/3rd points to the Monge point |
| "EulerProjected" | feet of the Euler points |
| "Excentral" | centers of excircles, also called the excenters |
| "Extouch" | tangency points of excircles |
| "Fermat" | extensions of the Fermat point |
| "Feuerbach" | sphere intangency points with exspheres |
| "HalfAltitude" | midpoints of altitudes |
| "Incentral" | cevians of incenter |
| "Medial" | centroids of the component triangles |
| "Negative" | reflection of vertices via the centroid |
| "Reflection" | reflection of vertices via the opposite faces |
| "Symmedial" | cevians of symmedian point |
Examples
Basic Examples (2)
Find the anticomplementary tetrahedron:
| In[1]:= | ![tet = {{0, 0, 0}, {0, 0, 6}, {0, 8, 6}, {6, 2, 9}};
anti = ResourceFunction["SubTetrahedron"][tet, "Anticomplementary"]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/128c5ad094866ec3.png){kind=small} |
| Out[2]= |  |
Show it:
| In[3]:= | ![Graphics3D[{Opacity[.5], Blue, Tetrahedron[tet], Opacity[0], Tetrahedron[anti]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/11922c3df0338d1e.png){kind=small} |
| Out[3]= |  |
Scope (4)
Find the reflection tetrahedron:
| In[4]:= | ![tet = {{0, 0, 0}, {1, 2, 0}, {3, 0, 0}, {1, 1, 2}};
ref = ResourceFunction["SubTetrahedron"][tet, "Reflection"]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/1147b725f752e56e.png) |
| Out[5]= |  |
Show both tetrahedra and the reflected vertices:
| In[6]:= | ![Graphics3D[{ Opacity[1], Tube[#] & /@ Transpose[{tet, ref}], Opacity[.1], Blue, Tetrahedron[tet], Red, Tetrahedron[ref]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/6b2eb7baf8d76d65.png) |
| Out[6]= |  |
Find the altitude tetrahedron:
| In[7]:= | ![initial = {{0, 0, 0}, {1, 2, 0}, {3, 0, 0}, {1, 1, 2}};
alt = ResourceFunction["SubTetrahedron"][initial, "Altitude"]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/47f1db65030038d4.png) |
| Out[8]= |  |
Show both tetrahedra and the altitudes:
| In[9]:= | ![Graphics3D[{Tube[#] & /@ Transpose[{initial, alt}], Opacity[.1], Blue,
Tetrahedron[initial], Red, Tetrahedron[alt]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/6e3b06d79439c763.png) |
| Out[9]= |  |
Find and show the BCI tetrahedron:
| In[10]:= | ![tet = {{0, 0, 0}, {0, 0, 6}, {0, 8, 6}, {6, 2, 9}};
bci = N[ResourceFunction["SubTetrahedron"][tet, "BCI"]]; Graphics3D[{Opacity[.5], Tetrahedron[tet], Tetrahedron[bci], Sphere[#, (EuclideanDistance @@ Take[bci, 2])/2] & /@ bci}, Boxed -> False, ImageSize -> Small, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/705fc04079d7e938.png) |
| Out[11]= |  |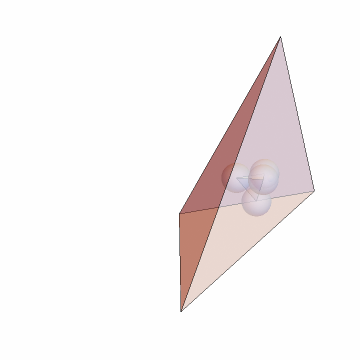
Find and show the symmedial tetrahedron:
| In[12]:= | ![initial = Tetrahedron[{{0, 0, 0}, {1, 2, 0}, {3, 0, 0}, {1, 1, 2}}];
sym = ResourceFunction["SubTetrahedron"][initial, "Symmedial"]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/6c38c7a91eadf32f.png) |
| Out[13]= |  |
| In[14]:= | ![Graphics3D[{EdgeForm[Black], White, Opacity[.5], initial, EdgeForm[Green], Tetrahedron[sym]}]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/6b93cf244c1030cf.png){kind=small} |
| Out[14]= |  |
Neat Examples (2)
Find the Euler, EulerProjected and Medial tetrahedra:
| In[15]:= | ![initial = {{0, 0, 0}, {1, 3, 0}, {3, 0, 0}, {1, 1, 2}};
tetras = ResourceFunction["SubTetrahedron"][initial, #] & /@ {"Euler", "EulerProjected", "Medial"}](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/7a7c0cb2f4eb3e78.png) |
| Out[16]= |  |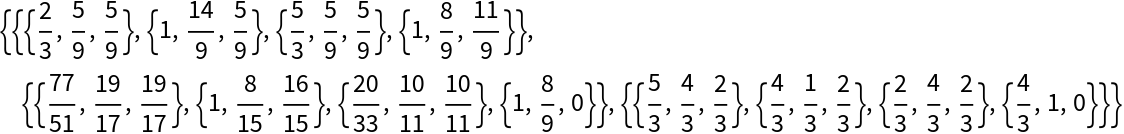
All have the same circumsphere:
| In[17]:= |  |
| Out[17]= |  |
Show the 12-point sphere:
| In[18]:= | ![Graphics3D[{Opacity[.2], Thick, Tetrahedron[initial], spheres[[1]], Tetrahedron /@ tetras}, Boxed -> False, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/27c3066c30e7f9b4.png) |
| Out[18]= |  |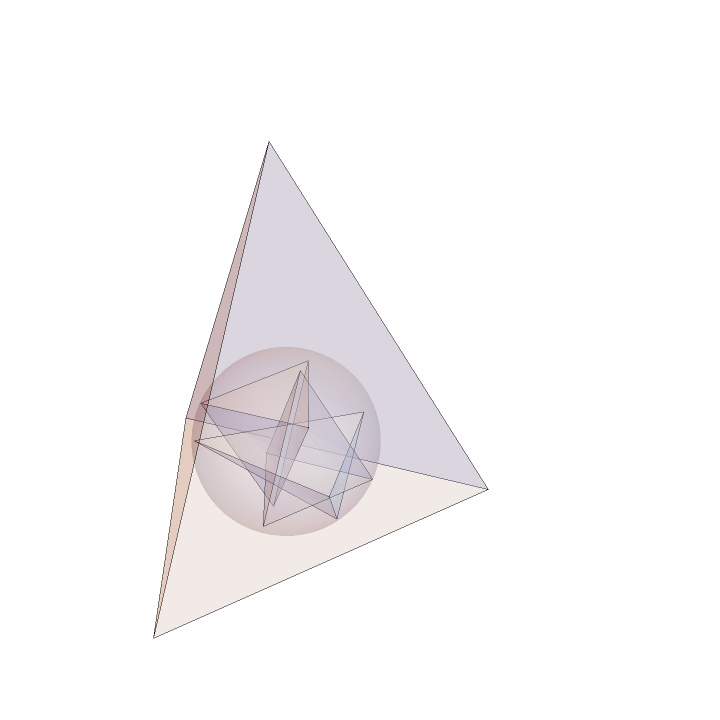
This tetrahedron is close to being similar to the reflected tetrahedron:
| In[19]:= | ![tet = {{0, 0, 0}, {1, 0, 0}, {0.8029, 2.8552, -2.6304}, {2.2197, 1.0925, 1.0949}};
ref = ResourceFunction["SubTetrahedron"][tet, "Reflection"];
Graphics3D[{Opacity[.5], Tetrahedron[tet], Tetrahedron[ref]}, Boxed -> False, ImageSize -> Medium, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1-1-0/47275dfe333ff7e9.png) |
| Out[20]= |  |
Requirements
Wolfram Language 13.0 (December 2021) or above
Version History
Related Resources
Related Symbols
License Information
This work is licensed under a Creative Commons Attribution 4.0 International License