Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SubTetrahedron (1.0.0) current version: 1.2.0 »

Source Notebook

Construct special tetrahedra of a tetrahedron

Contributed by: Ed Pegg Jr

ResourceFunction["SubTetrahedron"][tetra, "special"]

returns the tetrahedron identified by "special" from the tetrahedron tetra.

Details

For a tetrahedron ABCD, various special tetrahedra are defined:
"Altitude"feet of the altitudes
"Anticomplementary"tetrahedron with ABCD as medial tetrahedron
"BCI"centers of four tangent spheres of equal size
"Circummedial"circumcevian tetrahedron of the centroid
"Circummonge"circumcevian tetrahedron of the Monge point
"Contact"tangency points of insphere
"Euler"2/3rd points to the Monge point
"EulerProjected"feet of the Euler points
"Excentral"centers of excircles, also called the excenters
"Extouch"tangency points of excircles
"Feuerbach"sphere intangency points with exspheres
"HalfAltitude"midpoints of altitudes
"Incentral"cevians of incenter
"Medial"centroids of the component triangles
"Negative"reflection of vertices via the centroid
"Reflection"reflection of vertices via the opposite faces
"Symmedial"cevians of symmedian point

Examples

Basic Examples (2) 

Find the anticomplementary tetrahedron:

In[1]:=
tet = {{0, 0, 0}, {0, 0, 6}, {0, 8, 6}, {6, 2, 9}}; anti = ResourceFunction["SubTetrahedron"][tet, "Anticomplementary"]
Out[2]=

Show it:

In[3]:=
Graphics3D[{Opacity[.5], Blue, Tetrahedron[tet], Opacity[0], Tetrahedron[anti]}, Sequence[ Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]
Out[3]=

Scope (4) 

Find the reflection tetrahedron:

In[4]:=
tet = {{0, 0, 0}, {1, 2, 0}, {3, 0, 0}, {1, 1, 2}}; ref = ResourceFunction["SubTetrahedron"][tet, "Reflection"]
Out[5]=

Show both tetrahedra and the reflected vertices:

In[6]:=
Graphics3D[{ Opacity[1], Tube[#] & /@ Transpose[{tet, ref}], Opacity[.1], Blue, Tetrahedron[tet], Red, Tetrahedron[ref]}, Sequence[ Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]
Out[6]=

Find the altitude tetrahedron:

In[7]:=
initial = {{0, 0, 0}, {1, 2, 0}, {3, 0, 0}, {1, 1, 2}}; alt = ResourceFunction["SubTetrahedron"][initial, "Altitude"]
Out[8]=

Show both tetrahedra and the altitudes:

In[9]:=
Graphics3D[{Tube[#] & /@ Transpose[{initial, alt}], Opacity[.1], Blue, Tetrahedron[initial], Red, Tetrahedron[alt]}, Sequence[ Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]
Out[9]=

Find and show the BCI tetrahedron:

In[10]:=
tet = {{0, 0, 0}, {0, 0, 6}, {0, 8, 6}, {6, 2, 9}}; bci = N[ResourceFunction["SubTetrahedron"][tet, "BCI"]]; Graphics3D[{Opacity[.5], Tetrahedron[tet], Tetrahedron[bci], Sphere[#, (EuclideanDistance @@ Take[bci, 2])/2] & /@ bci}, Boxed -> False, ImageSize -> Small, SphericalRegion -> True]
Out[11]=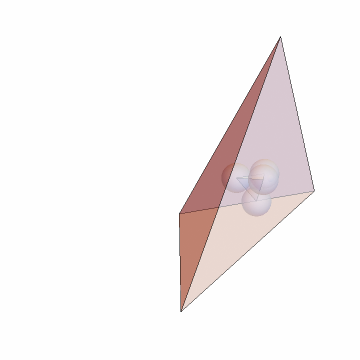

Find and show the symmedial tetrahedron:

In[12]:=
initial = {{0, 0, 0}, {1, 2, 0}, {3, 0, 0}, {1, 1, 2}}; sym = ResourceFunction["SubTetrahedron"][initial, "Symmedial"]
Out[12]=
In[13]:=
Graphics3D[{EdgeForm[Black], White, Opacity[.5], Tetrahedron@initial, EdgeForm[Green], Tetrahedron@sym}]
Out[13]=

Neat Examples (2) 

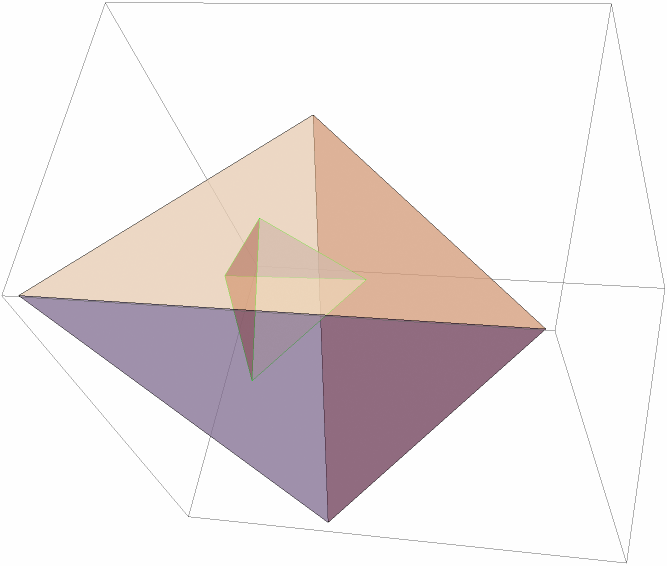Find the Euler, EulerProjected and Medial tetrahedra:

In[14]:=
initial = {{0, 0, 0}, {1, 3, 0}, {3, 0, 0}, {1, 1, 2}}; tetras = ResourceFunction["SubTetrahedron"][initial, #] & /@ {"Euler", "EulerProjected", "Medial"}
Out[15]=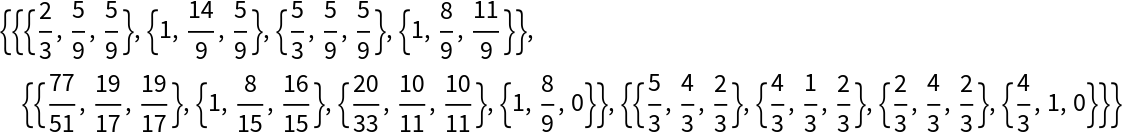

All have the same circumsphere:

In[16]:=
spheres = Circumsphere /@ tetras
Out[16]=

Show the 12-point sphere:

In[17]:=
Graphics3D[{Opacity[.2], Thick, Tetrahedron[initial], spheres[[1]], Tetrahedron /@ tetras}, Boxed -> False, SphericalRegion -> True]
Out[17]=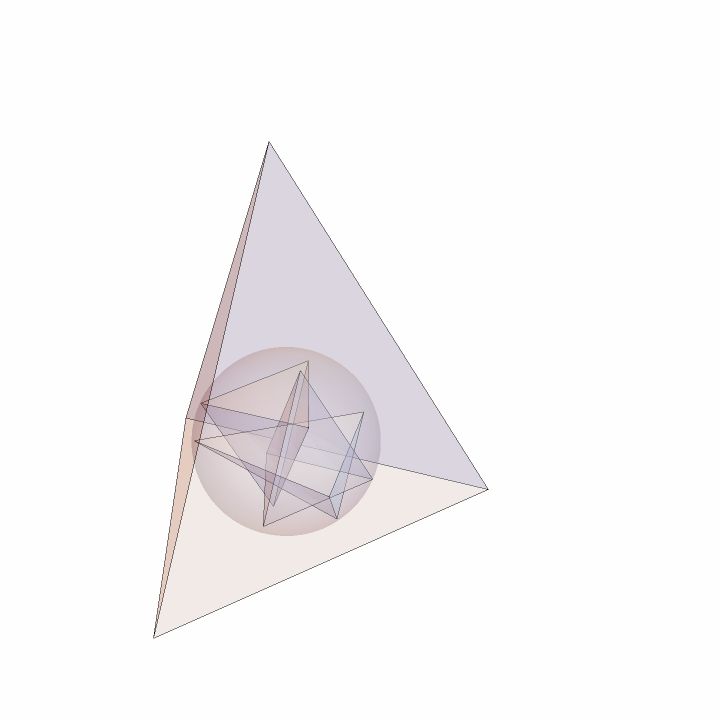

This tetrahedron is close to being similar to the reflected tetrahedron:

In[18]:=
tet = {{0, 0, 0}, {1, 0, 0}, {0.8029, 2.8552, -2.6304}, {2.2197, 1.0925, 1.0949}}; ref = ResourceFunction["SubTetrahedron"][tet, "Reflection"]; Graphics3D[{Opacity[.5], Tetrahedron[tet], Tetrahedron[ref]}, Boxed -> False, ImageSize -> Medium, SphericalRegion -> True]
Out[19]=

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.2.0 – 31 October 2023
  • 1.1.0 – 27 October 2023
  • 1.0.0 – 18 October 2023

Related Resources

License Information