Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Construct special tetrahedra of a tetrahedron
ResourceFunction["SubTetrahedron"][tetra, "special"] returns the tetrahedron identified by "special" from the tetrahedron tetra. |
| "Altitude" | feet of the altitudes |
| "Anticomplementary" | tetrahedron with ABCD as medial tetrahedron |
| "BCI" | centers of four tangent spheres of equal size |
| "Circummedial" | circumcevian tetrahedron of the centroid |
| "Circummonge" | circumcevian tetrahedron of the Monge point |
| "Contact" | tangency points of insphere |
| "Euler" | 2/3rd points to the Monge point |
| "EulerProjected" | feet of the Euler points |
| "Excentral" | centers of exspheres, also called the excenters |
| "Extangents" | tetrahedron externally tangent to expheres |
| "Extouch" | tangency points of exspheres |
| "Fermat" | extensions of the Fermat point |
| "Feuerbach" | sphere intangency points with exspheres |
| "HalfAltitude" | midpoints of altitudes |
| "Incentral" | cevians of incenter |
| "Medial" | centroids of the component triangles |
| "Negative" | reflection of vertices via the centroid |
| "Reflection" | reflection of vertices via the opposite faces |
| "Symmedial" | cevians of symmedian point |
| "Tangential" | tetrahedron tangent to circumsphere at vertices of ABCD |
Find the anticomplementary tetrahedron:
| In[1]:= |
| Out[2]= |
Show it:
| In[3]:= |
| Out[3]= |  |
Find and show the extouch tetrahedron, the tangent points for the exspheres:
| In[4]:= | ![tet = {{-22, -25, 4}, {-12, 15, -6}, {8, 5, -6}, {18, -15, 24}};
ex = ResourceFunction["SubTetrahedron"][tet, "Extouch"];
Graphics3D[{Opacity[.5], Tetrahedron[tet], Green, Tetrahedron[ex], Blue, ResourceFunction["Exspheres"][tet]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/64ed3421e23dde48.png) |
| Out[6]= | 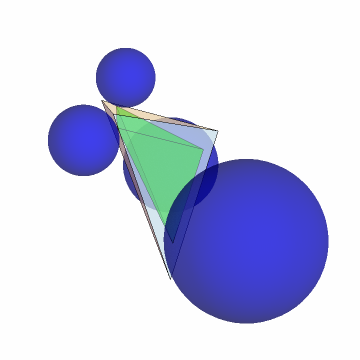 |
Find the reflection tetrahedron:
| In[7]:= | ![tet = {{0, 0, 0}, {1, 2, 0}, {3, 0, 0}, {1, 1, 2}};
ref = ResourceFunction["SubTetrahedron"][tet, "Reflection"]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1ee0822bac342fb9.png) |
| Out[8]= |
Show both tetrahedra and the reflected vertices:
| In[9]:= | ![Graphics3D[{ Opacity[1], Tube[#] & /@ Transpose[{tet, ref}], Opacity[.1], Blue, Tetrahedron[tet], Red, Tetrahedron[ref]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/2e1587f5aaf00a78.png) |
| Out[9]= |  |
Find the altitude tetrahedron:
| In[10]:= | ![initial = {{0, 0, 0}, {1, 2, 0}, {3, 0, 0}, {1, 1, 2}};
alt = ResourceFunction["SubTetrahedron"][initial, "Altitude"]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/6cf90d3638364a3e.png) |
| Out[11]= |
Show both tetrahedra and the altitudes:
| In[12]:= | ![Graphics3D[{Tube[#] & /@ Transpose[{initial, alt}], Opacity[.1], Blue,
Tetrahedron[initial], Red, Tetrahedron[alt]}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/4e2bae01dec977e1.png) |
| Out[12]= |  |
Find and show the BCI tetrahedron:
| In[13]:= | ![tet = {{0, 0, 0}, {0, 0, 6}, {0, 8, 6}, {6, 2, 9}};
bci = N[ResourceFunction["SubTetrahedron"][tet, "BCI"]]; Graphics3D[{Opacity[.5], Tetrahedron[tet], Tetrahedron[bci], Sphere[#, (EuclideanDistance @@ Take[bci, 2])/2] & /@ bci}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/11812789f71d97c9.png) |
| Out[14]= | 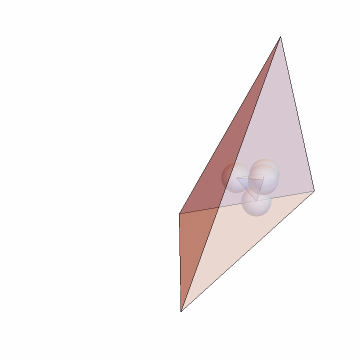 |
Find and show the symmedial tetrahedron:
| In[15]:= | ![initial = {{0, 0, 0}, {1, 2, 0}, {3, 0, 0}, {1, 1, 2}};
sym = ResourceFunction["SubTetrahedron"][initial, "Symmedial"]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/1b4a3e173cc95bc3.png) |
| Out[16]= |
| In[17]:= | ![Graphics3D[{EdgeForm[Black], White, Opacity[.5], Tetrahedron@initial, EdgeForm[Green], Tetrahedron@sym}, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/15fed73f3bf2d718.png) |
| Out[17]= | 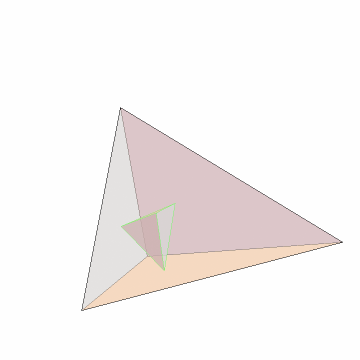 |
Find and show the tangential tetrahedron:
| In[18]:= | ![tet = {{0, 0, 0}, {0, 0, 6}, {0, 8, 6}, {6, 2, 9}};
tangential = ResourceFunction["SubTetrahedron"][tet, "Tangential"];
Graphics3D[{Opacity[.3], Circumsphere[tet], Opacity[.5], Blue, Tetrahedron[tet], Red, Tetrahedron[tangential] }, Sequence[
Boxed -> False, ImageSize -> Small, SphericalRegion -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/603ede05995f9d14.png) |
| Out[19]= |  |
Find the Euler, EulerProjected and Medial tetrahedra:
| In[20]:= | ![initial = {{0, 0, 0}, {1, 3, 0}, {3, 0, 0}, {1, 1, 2}};
tetras = ResourceFunction["SubTetrahedron"][initial, #] & /@ {"Euler", "EulerProjected", "Medial"}](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/241bd8808863bb63.png) |
| Out[21]= | 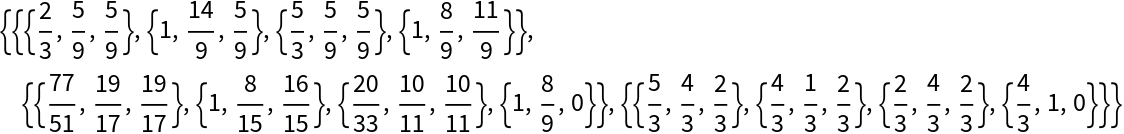 |
All have the same circumsphere:
| In[22]:= |
| Out[22]= |
Show the 12-point sphere:
| In[23]:= | ![Graphics3D[{Opacity[.2], Thick, Tetrahedron[initial], spheres[[1]], Tetrahedron /@ tetras}, Boxed -> False, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/283e24779fbfdb15.png) |
| Out[23]= | 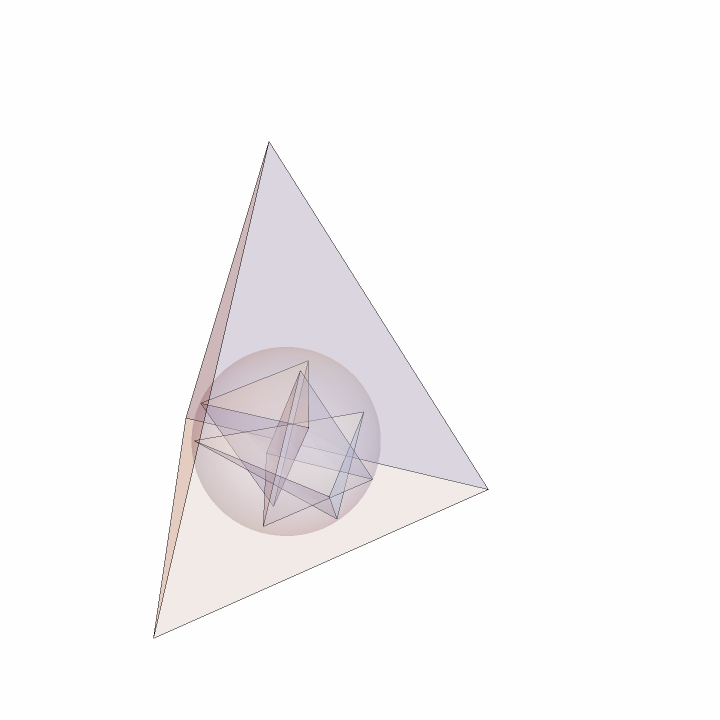 |
This tetrahedron is close to being similar to the reflected tetrahedron:
| In[24]:= | ![tet = {{0, 0, 0}, {1, 0, 0}, {0.8029, 2.8552, -2.6304}, {2.2197, 1.0925, 1.0949}};
ref = ResourceFunction["SubTetrahedron"][tet, "Reflection"];
Graphics3D[{Opacity[.5], Tetrahedron[tet], Tetrahedron[ref]}, Boxed -> False, ImageSize -> Medium, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/7ec96ffa1b2a5a43.png) |
| Out[25]= |  |
Find and show the extangents tetrahedron:
| In[26]:= | ![tet = {{0, 0, 0}, {0, 0, 6}, {0, 8, 6}, {6, 2, 9}};
extangents = ResourceFunction["SubTetrahedron"][tet, "Extangents"]; Graphics3D[{Tube[#] & /@ Transpose[{tet, extangents}], Opacity[.3], Blue, Tetrahedron[tet], Red, Tetrahedron[extangents], Green, ResourceFunction["Exspheres"][tet]}, Boxed -> False, ImageSize -> Medium, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/7d88458421f13102.png) |
| Out[27]= | 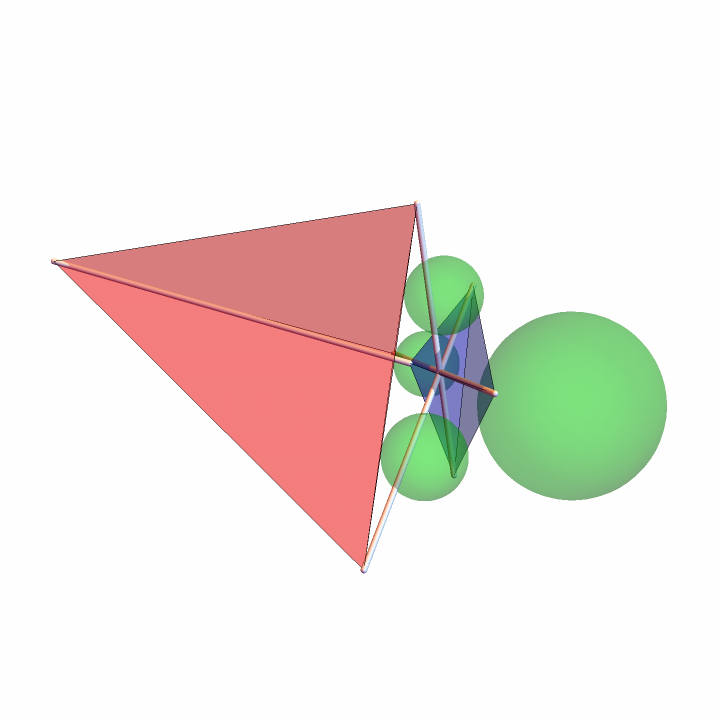 |
Find the perspector of the tetrahedron and its extangents tetrahedron:
| In[28]:= | ![RootApproximant /@ Mean[First[RegionIntersection @@ #] & /@ Subsets[InfiniteLine[#] & /@ Transpose[{tet, extangents}], {2}]]](https://www.wolframcloud.com/obj/resourcesystem/images/d23/d2329ecd-3568-43e0-bafb-abdba86c43dd/2066bb59ff96906e.png) |
| Out[28]= |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License