Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Calculate the Student's t-value that corrects for the bias of the unknown standard deviation in the statistical uncertainty of a measurement
ResourceFunction["StudentTValue"][ν] calculates the Student's t-value for a StudentTDistribution with ν degrees of freedom. | |
ResourceFunction["StudentTValue"][{v1,v2,…}] returns an Around created as by MeanAround with an error scaled by the Student’s t-value. |
Calculate the Student’s t-value for two degrees of freedom:
| In[1]:= |
| Out[1]= | 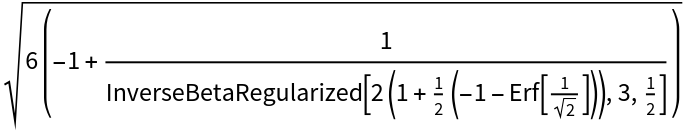 |
Scale the error of an around by the Student’s t-value:
| In[2]:= |
| Out[2]= |
Calculate the value of a measurement with a Student’s t-value scaled error:
| In[3]:= |
| Out[3]= |
The function can return an exact value in the single argument form. Use N to get a numerical value:
| In[4]:= |
| Out[4]= | 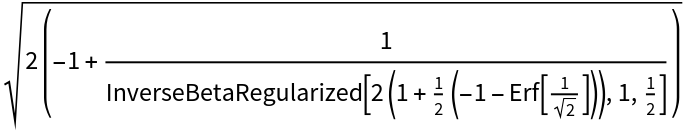 |
| In[5]:= |
| Out[5]= |
The function can handle a list of Around values:
| In[6]:= |
| Out[6]= |
StudentTValue can handle asymmetric Around:
| In[7]:= |
| Out[7]= |
StudentTValue will calculate the Student’s t-value according to the specified ConfidenceLevel (which is per default at 0.683…=1σ):
| In[8]:= |
| Out[8]= |
Calculate the statistical uncertainty for measurements with only a few data points:
| In[9]:= |
| Out[10]= |
The Student’s t-value for a List is equal to the Student’s t-value of the resulting MeanAround of the data with the degrees of freedom equal to the number of data points minus one:
| In[11]:= | ![ResourceFunction["StudentTValue"][{1, 2, 3, 4, 3, 2, 1}] === ResourceFunction["StudentTValue"][7 - 1, MeanAround[{1, 2, 3, 4, 3, 2, 1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/951/951a3c37-532c-42b5-8114-4dbb2bfdb3b4/305fff5a4cf673a4.png) |
| Out[11]= |
For many measurements, StudentTValue will tend towards one (if the ConfidenceLevel option is set to Automatic as default):
| In[12]:= |
| Out[12]= | 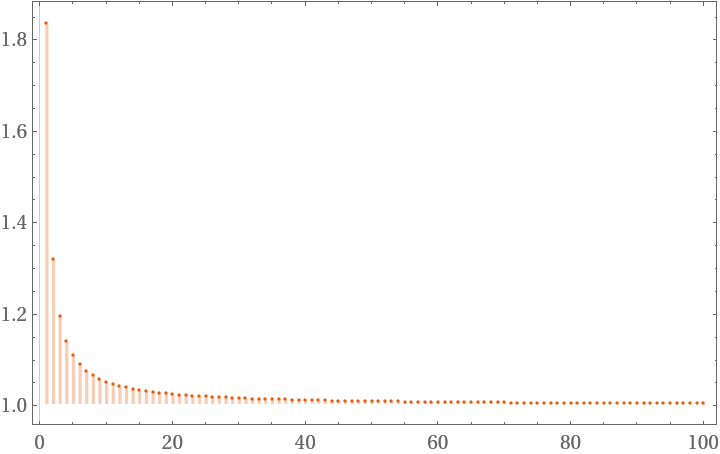 |
The function only accepts integers as the degree of freedom parameter ν:
| In[13]:= |
| Out[13]= |
The function returns an infinitely-big error interval for just one value:
| In[14]:= |
| Out[14]= |
The error interval from StudentTValue always encloses the one from MeanAround but converges for a high enough number of measurements:
| In[15]:= | ![list = RandomVariate[NormalDistribution[1, 0.2], 20];
ListPlot[
Transpose[({ResourceFunction["StudentTValue"][#], MeanAround[#]} &@
list[[1 ;; #]]) & /@ Range[2, Length[list]]], IntervalMarkers -> "Bands", PlotRange -> {{0, 20}, {0.8, 1.2}}]](https://www.wolframcloud.com/obj/resourcesystem/images/951/951a3c37-532c-42b5-8114-4dbb2bfdb3b4/7195e2347da69c32.png) |
| Out[16]= | 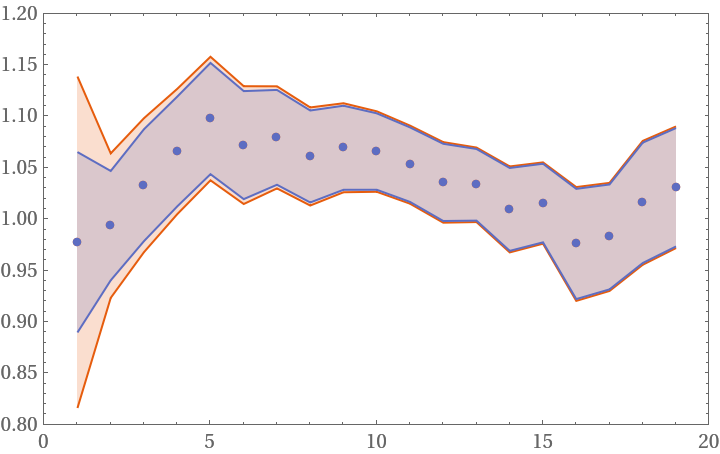 |
This work is licensed under a Creative Commons Attribution 4.0 International License