Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 StieltjesJacobiE

Source Notebook

Evaluate the Stieltjes-Jacobi polynomial

Contributed by: Jan Mangaldan

ResourceFunction["StieltjesJacobiE"][n,a,b,x]

gives the Stieltjes-Jacobi polynomial .

Details and Options

Mathematical function, suitable for both symbolic and numerical manipulation.
Explicit polynomials are given when possible.
The Stieltjes-Jacobi polynomial is the polynomial whose roots are the additional abscissas in Jacobi-Kronrod quadrature, apart from the abscissas that are the roots of the Jacobi polynomial .
is a polynomial of degree n+1.
For certain special arguments, ResourceFunction["StieltjesJacobiE"] automatically evaluates to exact values.
ResourceFunction["StieltjesJacobiE"] can be evaluated to arbitrary numerical precision.
ResourceFunction["StieltjesJacobiE"] automatically threads over lists.

Examples

Basic Examples (2) 

Compute the 2nd Stieltjes-Jacobi polynomial:

In[1]:=
ResourceFunction["StieltjesJacobiE"][2, a, b, z]
Out[1]=

Plot over a subset of the reals:

In[2]:=
Plot[ResourceFunction["StieltjesJacobiE"][10, 2, 2, x], {x, -1, 1}]
Out[2]=

Scope (4) 

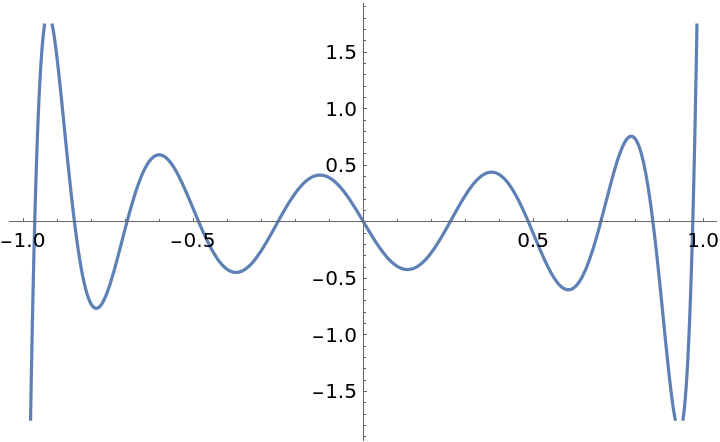Evaluate numerically:

In[3]:=
ResourceFunction["StieltjesJacobiE"][9, 1, 3, 1.5]
Out[3]=

Evaluate to high precision:

In[4]:=
N[ResourceFunction["StieltjesJacobiE"][9, 1, 3, 3/2], 30]
Out[4]=

The precision of the output tracks the precision of the input:

In[5]:=
ResourceFunction[ "StieltjesJacobiE"][9, 1, 3, 1.5000000000000000000000000000]
Out[5]=

StieltjesJacobiE threads elementwise over lists:

In[6]:=
ResourceFunction["StieltjesJacobiE"][{1, 2, 3}, 4, 5, z]
Out[6]=

Applications (2) 

Compute the abscissas and weights of a (2n+1)-point Gauss-Kronrod quadrature:

In[7]:=
n = 7; a1 = x /. NSolve[LegendreP[n, x] == 0, x, WorkingPrecision -> 25]; a2 = x /. NSolve[ResourceFunction["StieltjesJacobiE"][n, 0, 0, x] == 0, x, WorkingPrecision -> 25];
In[8]:=
ck = N[(2^(n + 1) n!)/(2 n + 1)!!, 25]; w1 = 4/(n (n + 1) LegendreP[n - 1, a1] JacobiP[n - 1, 1, 1, a1]) + ( 2 ck)/((n + 1) JacobiP[n - 1, 1, 1, a1] ResourceFunction[ "StieltjesJacobiE"][n, 0, 0, a1]); w2 = ck/(LegendreP[n, a2] ((\!\( \*SubscriptBox[\(\[PartialD]\), \(x\)]\(\* InterpretationBox[ TagBox[ DynamicModuleBox[{Typeset`open = False}, FrameBox[ PaneSelectorBox[{False->GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["StieltjesJacobiE", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource[ "FEBitmaps", "IconizeCloser"], ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource[ "FEBitmaps", "IconizeOpener"], ImageSizeCache->{11., {1., 10.}}]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{ {GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["StieltjesJacobiE", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource[ "FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource[ "FEBitmaps", "IconizeOpener"]]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]}, { StyleBox[ PaneBox[GridBox[{ { RowBox[{ TagBox["\<\"Version (latest): \"\>", "IconizedLabel"], " ", TagBox["\<\"1.0.0\"\>", "IconizedItem"]}]}, { TagBox[ TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/9d3a68d3-524a-49a1-8296-13dcb7312c01/"}, "HyperlinkURL"], "IconizedItem"]} }, DefaultBaseStyle->"Column", GridBoxAlignment->{"Columns" -> {{Left}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle", FontFamily->"Roboto", FontSize->11]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, { GrayLevel[0.8]}, False}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open], BaselinePosition->Baseline, ImageSize->Automatic], Background->RGBColor[ 0.9686274509803922, 0.9764705882352941, 0.984313725490196], BaselinePosition->Baseline, DefaultBaseStyle->{}, FrameMargins->{{0, 0}, {1, 0}}, FrameStyle->RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627], RoundingRadius->4]], {"FunctionResourceBox", RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784], "StieltjesJacobiE"}, TagBoxNote->"FunctionResourceBox"], ResourceFunction["StieltjesJacobiE"], BoxID -> "StieltjesJacobiE", Selectable->False][n, 0, 0, x]\)\)) /. x -> a2));
In[9]:=
ab = Riffle[a2, a1]
Out[9]=
In[10]:=
wt = Riffle[w2, w1]
Out[10]=

Use the Gauss-Kronrod abscissas and weights to approximate the area under a curve:

In[11]:=
f = x |-> Cos[x] + 3 x^3 - x + 3; a = -1/2; b = 3/2;
In[12]:=
res = ((b - a)/2) wt . f[Rescale[ab, {-1, 1}, {a, b}]]
Out[12]=

Compare to the output of NIntegrate:

In[13]:=
NIntegrate[f[x], {x, a, b}, WorkingPrecision -> 25]
Out[13]=
In[14]:=
Abs[% - res]
Out[14]=

Compute the abscissas and weights of a (2n+1)-point Lobatto-Kronrod quadrature:

In[15]:=
n = 7; a1 = x /. NSolve[JacobiP[n - 1, 1, 1, x] == 0, x, WorkingPrecision -> 25]; a2 = x /. NSolve[ResourceFunction["StieltjesJacobiE"][n - 1, 1, 1, x] == 0, x, WorkingPrecision -> 25];
In[16]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/a01ac0ea-2246-4b84-a291-892c90db6706"]
In[17]:=
ab = Join[{N[-1, 25]}, Riffle[a2, a1], {N[1, 25]}]
Out[17]=
In[18]:=
wt = Riffle[w1, w2]
Out[18]=

Use the Lobatto-Kronrod abscissas and weights to approximate the area under a curve:

In[19]:=
f = x |-> Cos[x] + 3 x^3 - x + 3; a = -1/2; b = 3/2;
In[20]:=
res = ((b - a)/2) wt . f[Rescale[ab, {-1, 1}, {a, b}]]
Out[20]=

Compare to the output of NIntegrate:

In[21]:=
NIntegrate[f[x], {x, a, b}, WorkingPrecision -> 25]
Out[21]=
In[22]:=
Abs[% - res]
Out[22]=

Properties and Relations (3) 

The second (nonpolynomial) solution of the Jacobi differential equation, :

In[23]:=
JacobiQ[n_, a_, b_, x_] := 2^-n (x - 1)^-(a + n + 1) (x + 1)^-b Hypergeometric2F1[a + n + 1, n + 1, a + b + 2 n + 2, 2/(1 - x)]

StieltjesJacobiE is the polynomial part of the asymptotic expansion of at Infinity:

In[24]:=
Normal[Quiet@ Series[1/((x - 1)^a (x + 1)^b JacobiQ[2, a, b, x]), {x, \[Infinity], 0}]]
Out[24]=
In[25]:=
% == ResourceFunction["StieltjesJacobiE"][2, a, b, x] // Simplify
Out[25]=

StieltjesJacobiE is a polynomial of degree n+1:

In[26]:=
Exponent[ResourceFunction["StieltjesJacobiE"][6, \[Alpha], \[Beta], x], x]
Out[26]=

The roots of JacobiP and StieltjesJacobiE interlace each other:

In[27]:=
Plot[{ResourceFunction["StieltjesJacobiE"][5, 1, 1, x], JacobiP[5, 1, 1, x]}, {x, -1, 1}]
Out[27]=

Neat Examples (1) 

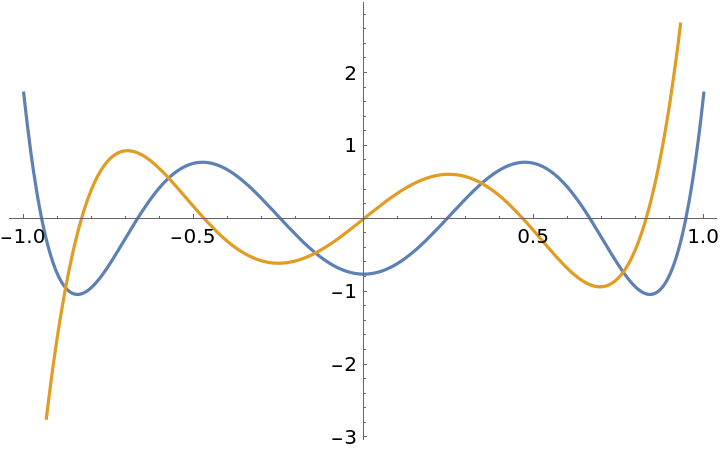A curve with multiple loops:

In[28]:=
ParametricPlot[{ResourceFunction["StieltjesJacobiE"][4, 0, 0, Cos[t]], ResourceFunction["StieltjesJacobiE"][4, 0, 0, Sin[t]]}, {t, 0, 2 \[Pi]}]
Out[28]=

Version History

  • 1.0.0 – 04 January 2021

Source Metadata

  • Citation:
    • Monegato G., A note on extended Gaussian quadrature rules. Mathematics of Computation, vol. 30, 812-817, 1976
      DOI: 10.1090/S0025-5718-1976-0440878-3
    • Monegato G., Some remarks on the construction of extended Gaussian quadrature rules. Mathematics of Computation, vol. 32, 247-252, 1978
      DOI: 10.1090/S0025-5718-1978-0458810-7

Related Resources

License Information