Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the stationary points of a function of one or more variables
ResourceFunction["StationaryPoints"][expr, {var1,var2, …}] computes the stationary points of expr with respect to the variables vari. | |
ResourceFunction["StationaryPoints"][{expr,domain},{var1,var2,…}] computes the stationary points of expr that lie within the specified domain. | |
ResourceFunction["StationaryPoints"][…, "type"] limits the stationary points returned to those of the given type. |
Find the stationary points of a function of one variable:
| In[1]:= |
| Out[1]= |
Plot the function and its stationary points found above:
| In[2]:= | ![Plot[t^2 Exp[-t^2], {t, -5, 5}, Epilog -> Join[{Red, PointSize@Large}, Point[{#[[2, 1, 2]], #[[1]]}] & /@ Flatten[Values[statPoints], 1]]]](https://www.wolframcloud.com/obj/resourcesystem/images/871/8716575d-4f76-42ed-b088-eb35860223e2/5-0-0/0df6781f495d3587.png) |
| Out[2]= | 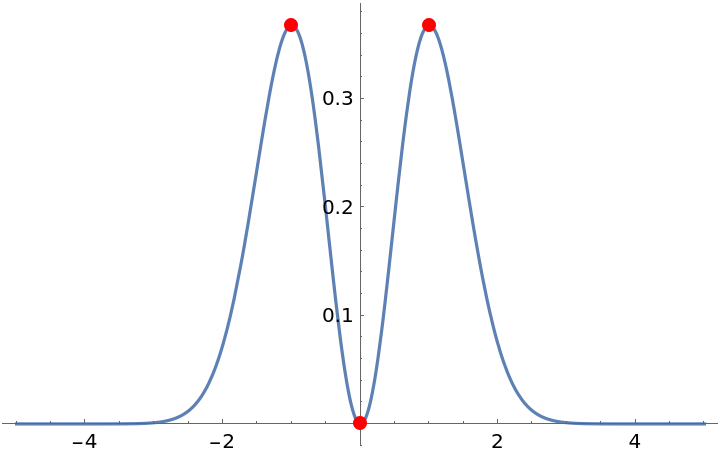 |
Find the stationary points of a periodic function:
| In[3]:= |
| Out[3]= | 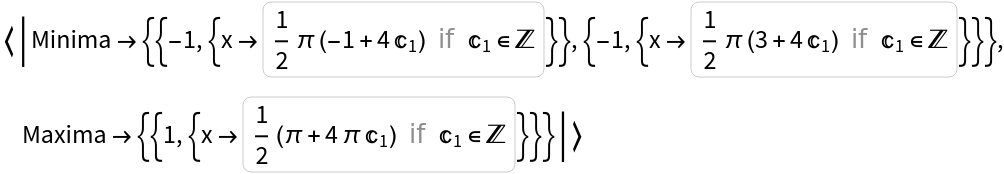 |
| In[4]:= |
| Out[4]= |
Find the stationary points of a function over a restricted domain:
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
Find stationary points of a function of two variables:
| In[7]:= |
| Out[7]= |
Find stationary points of a function of three variables when restricting to a plane:
| In[8]:= |
| Out[8]= |
Using the "Type" option will return only stationary points of the given type:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= | 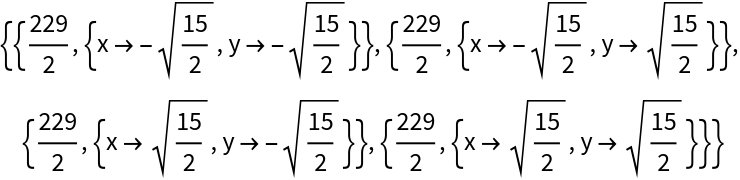 |
| In[11]:= |
| Out[11]= |
Using Automatic as the second argument gives an Association of all stationary points:
| In[12]:= |
| Out[12]= | 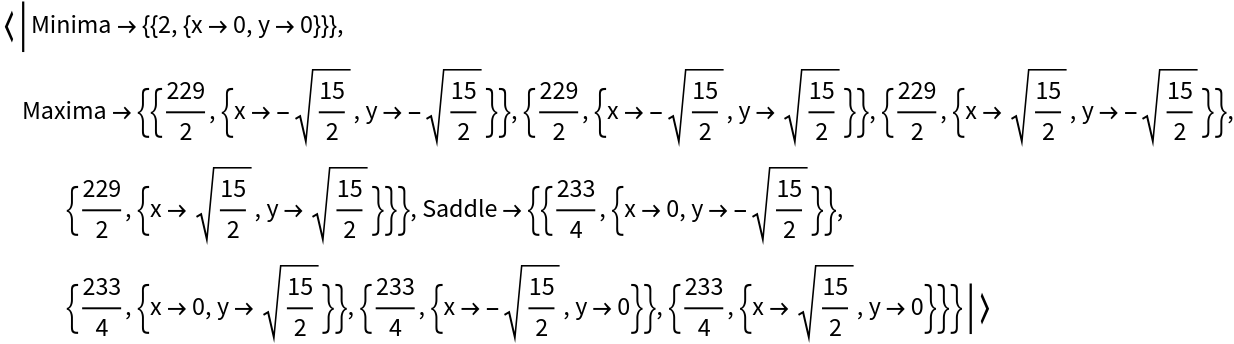 |
StationaryPoints will sometimes return results in terms of Root objects:
| In[13]:= |
| Out[13]= |  |
Results such as these can be numericized by applying N:
| In[14]:= |
| Out[14]= |
For functions with a repeating pattern of stationary points, StationaryPoints returns results in terms of one or more undetermined constants ci, which can take any integer value:
| In[15]:= |
| Out[15]= |
For functions possessing one or more families of non-isolated stationary points, StationaryPoints may return only the isolated stationary points. For example, the function sin(x3y3) has lines of stationary points along both the x- and y- axes, as can be seen in the following plot:
| In[16]:= |
| Out[16]= | 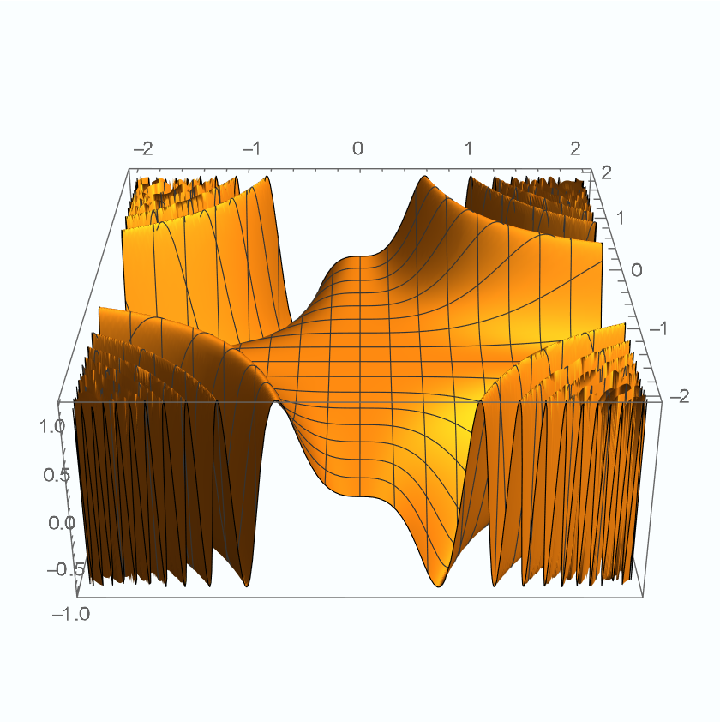 |
These, however, are excluded from the results of StationaryPoints:
| In[17]:= |
| Out[17]= | 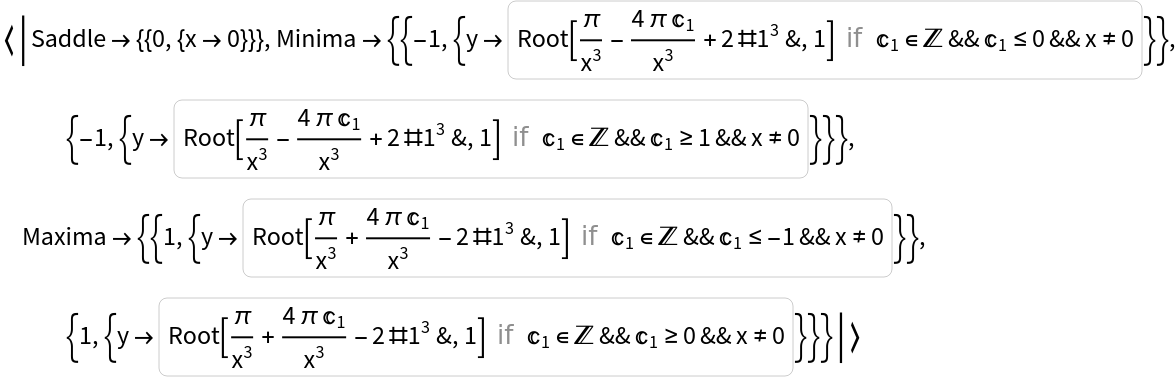 |
This work is licensed under a Creative Commons Attribution 4.0 International License