Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 StateMultipoleToDensityMatrix

Source Notebook

Represent state multipoles (statistical tensors) via density matrix elements

Contributed by: Xu-xing Geng

ResourceFunction["StateMultipoleToDensityMatrix"][j1,j2,k,q]

expand the state multipoles corresponding to the order-k irreducible tensor q-components with angular momenta j1 and j2 into density matrix elements.

Details

ResourceFunction["StateMultipoleToDensityMatrix"] expands the state multipole 𝒯[J,J]k,q corresponding to an angular momentum J1=J2=J into density matrix elements [J, J]m1,m2.
The state multipole is defined as the trace of the irreducible tensor: , where T is the irreducible tensor and  is the density matrix.
The state multipoles are expressed as linear combinations of density matrix elements, which can simplify the calculation of many physical quantities such as the expectation value of angular momentum and rotational symmetry analysis.
In experimental and theoretical studies, this relationship can help us extract angular momentum characteristics from experimental data (usually represented as a density matrix) and conduct in-depth analysis of the symmetry and physical properties of physical systems. It is particularly important in the fields of atomic physics and quantum optics.

Examples

Basic Examples (1) 

Expand the state multipole 𝒯[1,1]1,1 with angular momenta J1=1 and J2=1 into density matrix elements:

In[1]:=
ResourceFunction["StateMultipoleToDensityMatrix"][1, 1, 1, 1]
Out[1]=

Scope (1) 

Expand the state multipole 𝒯[1,2]1,1 with angular momenta J1=1 and J2=2 coupling into density matrix elements:

In[2]:=
ResourceFunction["StateMultipoleToDensityMatrix"][1, 2, 2, 0]
Out[2]=

Options (2) 

Expand all state multipole components of k=1 with momenta J1=1 and J2=1 into density matrix elements:

In[3]:=
Table[Subscript[\[ScriptCapitalT][1, 1], 1, j] == ResourceFunction["StateMultipoleToDensityMatrix"][1, 1, 1, j], {j, -1, 1}] // TableForm
Out[3]=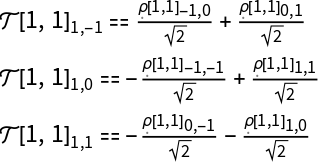

Expand all state multipole components of k=2 with momenta J1=3 and J2=4 into density matrix elements:

In[4]:=
Table[Subscript[\[ScriptCapitalT][3, 4], 2, j] == ResourceFunction["StateMultipoleToDensityMatrix"][3, 4, 2, j], {j, -2, 2}] // TableForm
Out[4]=

Publisher

Xuxing geng

Requirements

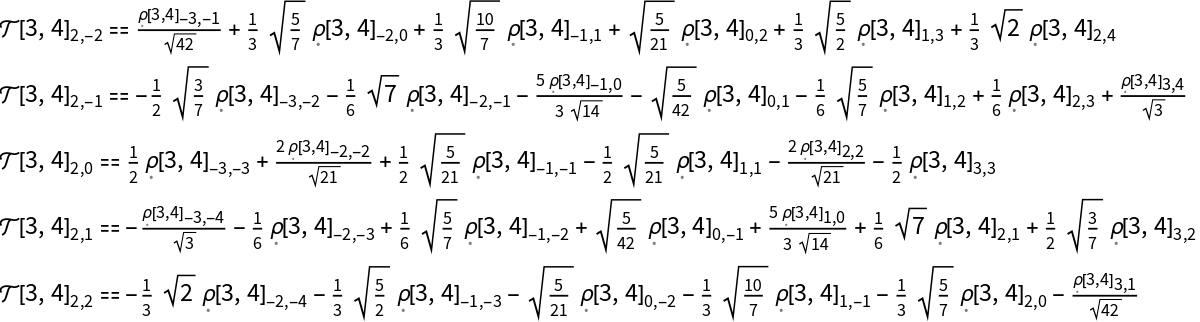Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 23 August 2024

Source Metadata

  • Citation:
    Blum K. Density matrix theory and applications[M]. Springer Science & Business Media, 2012.

Related Resources

License Information