Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 StandardSimplex

Source Notebook

Get the standard simplex for a specified dimension

Contributed by: Richard Hennigan (Wolfram Research)

ResourceFunction["StandardSimplex"][n]

gives the standard n-simplex embedded in .

ResourceFunction["StandardSimplex"][n,len]

gives the standard n-simplex with edge lengths of len.

ResourceFunction["StandardSimplex"][n,len,orientation]

orients the simplex according to orientation.

Details and Options

ResourceFunction["StandardSimplex"][n,…] gives Simplex[{v1,…,vn+1}], where each of the vi is a point in .
If no edge length is given, the resulting edge length will be .
In ResourceFunction["StandardSimplex"][n,len,orientation], valid values for orientation are:
1forward
-1reverse
Trueforward
Falsereverse

Examples

Basic Examples (5) 

Get the standard 0-simplex:

In[1]:=
ResourceFunction["StandardSimplex"][0]
Out[1]=

Get the standard 1-simplex:

In[2]:=
ResourceFunction["StandardSimplex"][1]
Out[2]=
In[3]:=
Graphics[%]
Out[3]=

Get the standard 2-simplex:

In[4]:=
ResourceFunction["StandardSimplex"][2]
Out[4]=
In[5]:=
Graphics3D[%]
Out[5]=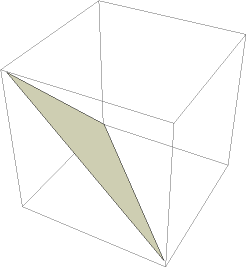

Get the standard 2-simplex with unit edge lengths:

In[6]:=
ResourceFunction["StandardSimplex"][2, 1]
Out[6]=

Get the standard 3-simplex with symbolic edge lengths:

In[7]:=
ResourceFunction["StandardSimplex"][3, a]
Out[7]=

Scope (3) 

Get a reverse orientation simplex:

In[8]:=
ResourceFunction["StandardSimplex"][2, 1, -1]
Out[8]=
In[9]:=
Graphics3D[{FaceForm[Red, Blue], %}]
Out[9]=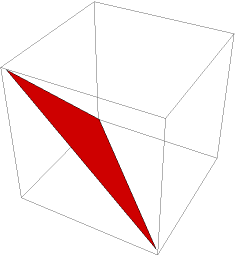

Compare to the canonical orientation:

In[10]:=
ResourceFunction["StandardSimplex"][2, 1, 1]
Out[10]=
In[11]:=
Graphics3D[{FaceForm[Red, Blue], %}]
Out[11]=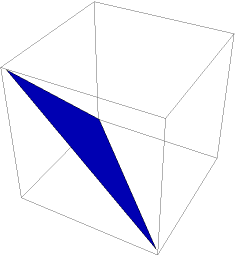

Forward orientation can be specified as 1, True or Automatic:

In[12]:=
ResourceFunction["StandardSimplex"][2, Automatic, 1]
Out[12]=
In[13]:=
ResourceFunction["StandardSimplex"][2, Automatic, True]
Out[13]=
In[14]:=
ResourceFunction["StandardSimplex"][2, Automatic, Automatic]
Out[14]=

Reverse orientation can be specified as -1 or False:

In[15]:=
ResourceFunction["StandardSimplex"][2, Automatic, -1]
Out[15]=
In[16]:=
ResourceFunction["StandardSimplex"][2, Automatic, False]
Out[16]=

Properties and Relations (2) 

The measure of StandardSimplex[n] is given by :

In[17]:=
Table[ResourceFunction["SimplexMeasure"][ ResourceFunction["StandardSimplex"][n]], {n, 0, 9}]
Out[17]=

The standard simplex becomes very small in higher dimensions:

In[18]:=
ListLinePlot[%]
Out[18]=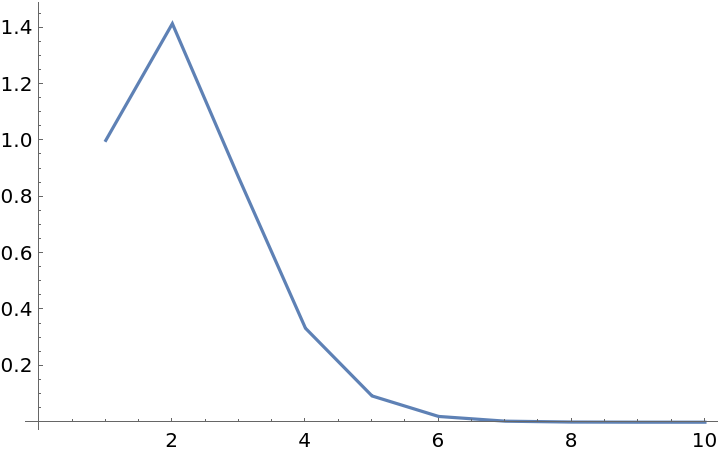

Inspect the orientations using ResourceFunction["SimplexOrientation"]:

In[19]:=
Table[ResourceFunction["SimplexOrientation"][ ResourceFunction["StandardSimplex"][n, Automatic, 1]], {n, 20}]
Out[19]=
In[20]:=
Table[ResourceFunction["SimplexOrientation"][ ResourceFunction["StandardSimplex"][n, Automatic, -1]], {n, 20}]
Out[20]=

Possible Issues (3) 

When n is zero, StandardSimplex will not return a Simplex, since Simplex will evaluate to a Point:

In[21]:=
ResourceFunction["StandardSimplex"][0]
Out[21]=
In[22]:=
Simplex[{{1}}]
Out[22]=

The 0-simplex has no edges to scale:

In[23]:=
ResourceFunction["StandardSimplex"][0, 1]
Out[23]=

The dimension specification must be a positive machine integer:

In[24]:=
ResourceFunction["StandardSimplex"][x, 1]
Out[24]=

Neat Examples (3) 

Visualize the boundary of the standard 2-simplex:

In[25]:=
ResourceFunction["SimplexBoundary"][ ResourceFunction["StandardSimplex"][2]]
Out[25]=
In[26]:=
Graphics3D[%]
Out[26]=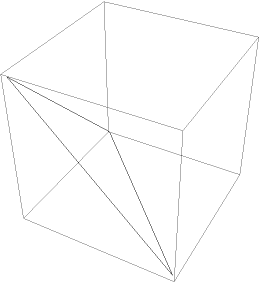

Project the standard 2-simplex into using an orthogonal projection:

In[27]:=
triangle = ResourceFunction["StandardSimplex"][2]
Out[27]=
In[28]:=
projected = Map[Most, triangle, {2}]
Out[28]=
In[29]:=
Graphics[projected]
Out[29]=

Project the standard 3-simplex into using an orthogonal projection:

In[30]:=
tetrahedron = ResourceFunction["StandardSimplex"][3]
Out[30]=
In[31]:=
projected = Map[Most, tetrahedron, {2}]
Out[31]=
In[32]:=
Graphics3D[projected]
Out[32]=

Requirements

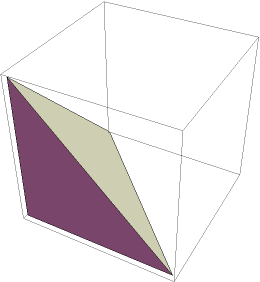Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 11 March 2019

Related Resources

License Information