Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SquareSpiralPoints

Source Notebook

Get the coordinates of the points on a square spiral with sides parallel to the axes

Contributed by: George Beck

ResourceFunction["SquareSpiralPoints"][n]

gives the list of coordinate pairs on a square spiral with n sides starting at the origin.

Details and Options

The list starts at the origin and goes up, left, down, right and repeats.

Examples

Basic Examples (4) 

Here are the points on the first four sides of the spiral:

In[1]:=
ResourceFunction["SquareSpiralPoints"][4]
Out[1]=

This shows the sequence of points in order on the first six sides:

In[2]:=
With[{s = ResourceFunction["SquareSpiralPoints"][6]}, Graphics[{{Pink, PointSize[.03], Point[s]}, Arrow@Partition[s, 2, 1]}]]
Out[2]=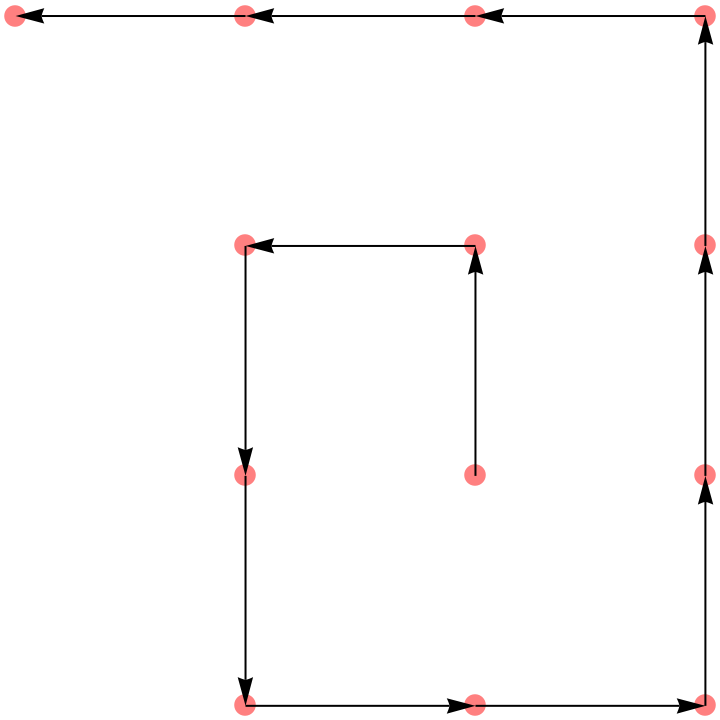

Forty black sides with 20 red sides overlaid:

In[3]:=
Graphics[{Line@ResourceFunction["SquareSpiralPoints"][40], Red, Line@ResourceFunction["SquareSpiralPoints"][20]}]
Out[3]=

The number of points in n sides:

In[4]:=
Length@ResourceFunction["SquareSpiralPoints"]@# & /@ Range[0, 10]
Out[4]=
In[5]:=
Table[Floor[(n + 1)^2/4] + 1, {n, 0, 10}]
Out[5]=

Neat Examples (2) 

This finds the coordinate pairs that are a prime distance along the square spiral:

In[6]:=
UlamSquareSpiralPoints[n_] := ResourceFunction["SquareSpiralPoints"][n][[ Prime@Range@PrimePi[Floor[(n + 1)^2/4] + 1] ]]

The larger points correspond to the primes 2, 3, 5, 7, 11, 13:

In[7]:=
With[{n = 6}, Graphics[{{LightGray, Line@ResourceFunction["SquareSpiralPoints"]@n}, Point@ResourceFunction["SquareSpiralPoints"]@n, PointSize[.08], Point@UlamSquareSpiralPoints@n}, ImageSize -> 100]]
Out[7]=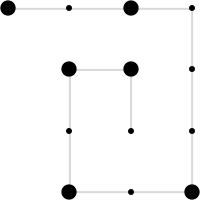

About 12% of the numbers up to 10101 are prime:

In[8]:=
With[{n = 200}, Floor[(n + 1)^2/4] + 1]
Out[8]=
In[9]:=
PrimePi@%
Out[9]=

Here are the first 1240 primes plotted along the square spiral:

In[10]:=
Graphics@Point@UlamSquareSpiralPoints@250
Out[10]=

About 11% of the numbers to 10101 are lucky:

In[11]:=
ResourceFunction["LuckyNumbers"]@10101 // Length
Out[11]=

This finds the coordinate pairs that are at lucky number distances along the square spiral:

In[12]:=
LuckySquareSpiralPoints[n_] := ResourceFunction["SquareSpiralPoints"][n][[ ResourceFunction["LuckyNumbers"][Floor[(n + 1)^2/4] + 1] ]]

Here are the first 1130 lucky numbers plotted along the square spiral:

In[13]:=
Graphics@Point@LuckySquareSpiralPoints@200
Out[13]=

Publisher

George Beck

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 26 February 2019

Related Resources

License Information