Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the final angle and spring length of a spring pendulum based on initial conditions
ResourceFunction["SpringPendulumFormula"][params,cond] computes the angle and spring length based on system parameters params and initial conditions cond. | |
ResourceFunction["SpringPendulumFormula"][property] returns the specified property of the spring pendulum formula. |
| k | "k" | spring constant |
| m | "m" | mass |
| l0 | "l0" | spring equalibrium length |
| li | "li" | initial spring length |
| t | "t" | final time |
| θi | "thetai" | initial angle from vertical |
| "Formula" | equations for spring pendulum |
| "QuantityVariableDimensions" | list of base dimensions for all variables |
| "QuantityVariableNames" | English names for all variables |
| "QuantityVariablePhysicalQuantities" | physical quantities for all variables |
| "QuantityVariables" | list of all variables |
| "QuantityVariableTable" | details on all variables |
Solve for the final spring length and final angle from the vertical for a spring pendulum:
| In[1]:= | ![ResourceFunction[
"SpringPendulumFormula"][<|"k" -> Quantity[100, "Newtons"/"Meters"], "l0" -> Quantity[1, "Meters"], "m" -> Quantity[1, "Kilograms"]|>, <|
"thetai" -> Quantity[55, "AngularDegrees"], "li" -> Quantity[1, "Meters"], "t" -> Quantity[6.1`, "Seconds"]|>]](https://www.wolframcloud.com/obj/resourcesystem/images/8d1/8d116b73-8333-44ec-b77b-09c538f2da60/366bc0ca2a472cac.png) |
| Out[1]= |  |
Specify gravitational acceleration:
| In[2]:= | ![ResourceFunction["SpringPendulumFormula"][
Association["k" -> Quantity[100, "Newtons"/"Meters"], "l0" -> Quantity[1, "Meters"], "m" -> Quantity[1, "Kilograms"], "g" -> Entity["Planet", "Mars"][
EntityProperty["Planet", "Gravity"]]], Association["thetai" -> Quantity[55, "AngularDegrees"], "li" -> Quantity[1, "Meters"], "t" -> Quantity[6.1`, "Seconds"]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8d1/8d116b73-8333-44ec-b77b-09c538f2da60/794299a22f2b7ed5.png) |
| Out[2]= |  |
Examine the equations of motion for a spring pendulum:
| In[3]:= |
| Out[3]= |
Find the quantity variables used by the SpringPendulumFormula:
| In[4]:= |
| Out[4]= |
Obtain their formal names:
| In[5]:= |
| Out[5]= |  |
Derive the physical quantities and unit dimensions of the variables:
| In[6]:= |
| Out[6]= |
| In[7]:= |
| Out[7]= |  |
Examine a table combining all the information about the quantity variables used or derived by SpringPendulumFormula:
| In[8]:= |
| Out[8]= |  |
Plot angle and length evolution over time:
| In[9]:= | ![result = ResourceFunction["SpringPendulumFormula"][
Association["k" -> Quantity[100, "Newtons"/"Meters"], "l0" -> Quantity[1, "Meters"], "m" -> Quantity[1, "Kilograms"]], Association["thetai" -> Quantity[55, "AngularDegrees"], "li" -> Quantity[1, "Meters"], "t" -> Quantity[6.1`, "Seconds"]]];](https://www.wolframcloud.com/obj/resourcesystem/images/8d1/8d116b73-8333-44ec-b77b-09c538f2da60/746cb4464c9b7c73.png) |
| In[10]:= |
| Out[10]= | 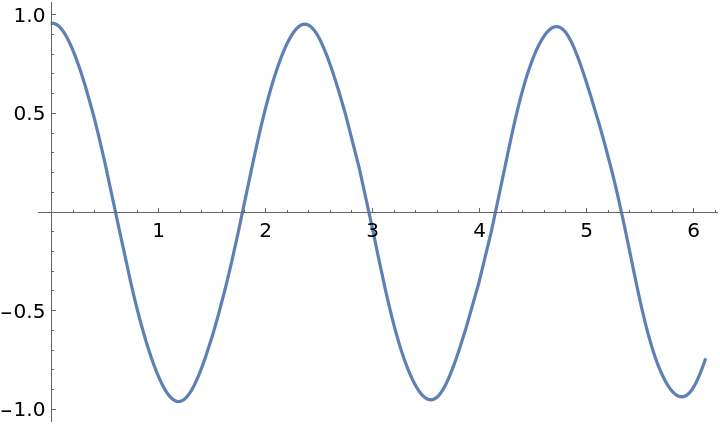 |
| In[11]:= |
| Out[11]= | 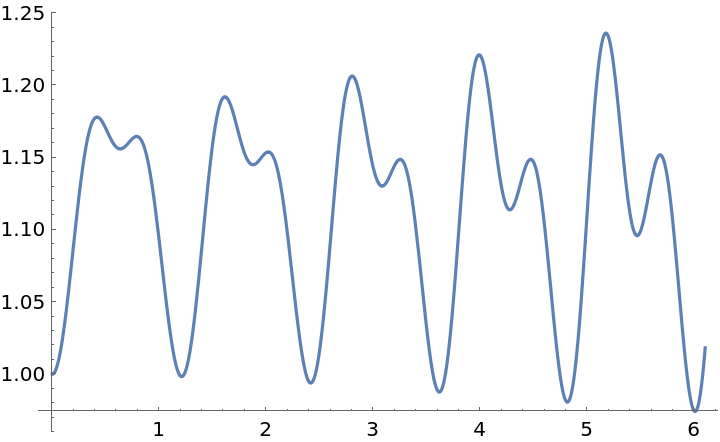 |
This work is licensed under a Creative Commons Attribution 4.0 International License