Function Repository Resource:

SplineCircle

Source Notebook

Generate a BSplineCurve primitive representing a circle

Contributed by: Carl Woll

ResourceFunction["SplineCircle"][{x,y}, r]

returns a BSplineCurve representation of a 2D circle with center {x,y} and radius r.

ResourceFunction["SplineCircle"][{x, y}, {r₁,r₂}]

returns a 2D ellipse with semimajor axis r₁ and semiminor axis r₂, and with the semimajor axis in the x direction.

ResourceFunction["SplineCircle"][{x, y}, {r₁,r₂}, u]

returns a 2D ellipse with the semimajor axis in the direction u.

ResourceFunction["SplineCircle"][{x, y}, {r₁,r₂}, u, {θ₁, θ₂}]

returns a 2D elliptical arc from θ₁ to θ₂ measured from the semimajor axis.

ResourceFunction["SplineCircle"][{x, y, z}, r]

returns a BSplineCurve representation of a 3D circle with center {x,y,z} and radius r, with the symmetry axis in the z direction.

ResourceFunction["SplineCircle"][{x, y, z},{r₁,r₂}]

returns a 3D ellipse with semimajor axis r₁ and semiminor axis r₂, and with the semimajor axis in the x direction.

ResourceFunction["SplineCircle"][{x, y, z},{r₁,r₂}, a]

returns a 3D ellipse with the symmetry axis in the direction a.

ResourceFunction["SplineCircle"][{x, y, z}, {r₁,r₂}, {u, v}]

returns a 3D ellipse with the semimajor axis in the direction u, and with the elliptical plane being spanned by u and v.

ResourceFunction["SplineCircle"][{x, y, z},{r₁,r₂}, p, {θ₁, θ₂}]

returns a 3D elliptical arc in the plane specified by p, where p can be the symmetry axis or the plane spanned by 3D vectors u and v.

Details and Options

Angles are measured counerclockwise from the semimajor axis direction.

In 2D, ResourceFunction["SplineCircle"][c,r,u] is equivalent to GeometricTransformation[Circle[c,r],RotationTransform[{{1,0},u},c]].

SplineCircle[c] is equivalent to SplineCircle[c, 1].

SplineCircle returns a BSplineCurve object.

SplineCircle can be used as a curve specification in primitives like Tube, Arrow, JoinedCurve and FilledCurve.

Examples

Basic Examples (7)

A 2D circle:

In[1]:=

Out[1]=

A 2D elliptical arc:

In[2]:=

Out[2]=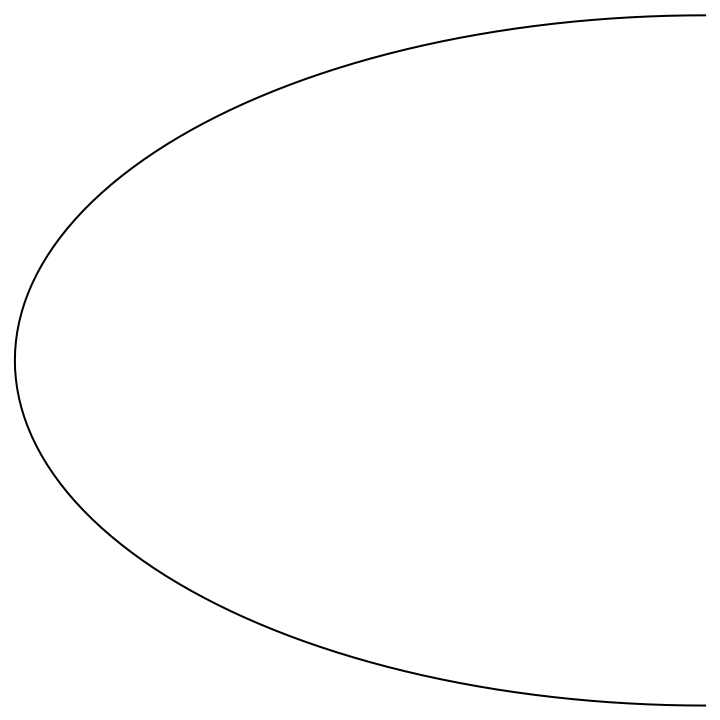

A 2D ellipse with semimajor axis in the direction {4, 1}:

In[3]:=

Out[3]=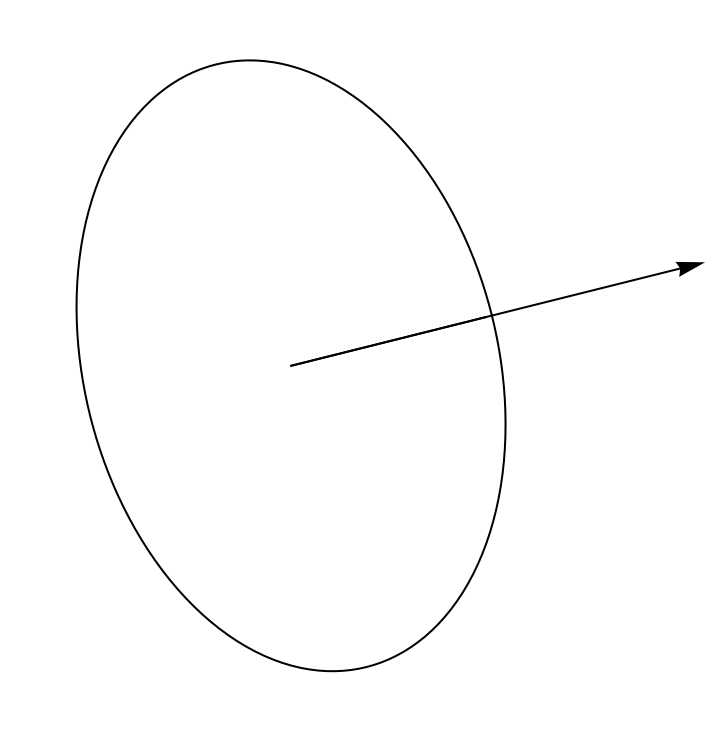

Differently styled ellipses:

In[4]:=

Out[4]=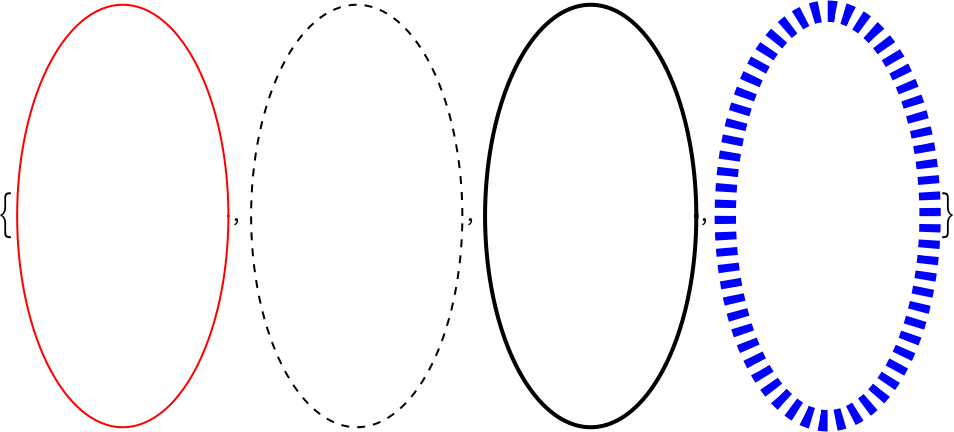

A 3D circle:

In[5]:=

Graphics3D[
ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{0, 0, 0}, 1],
Boxed -> False,
Axes -> True,
AxesOrigin -> {0, 0, 0},
AxesEdge -> {.5, .5, .5},
AxesLabel -> {x, y, z}
]

Out[5]=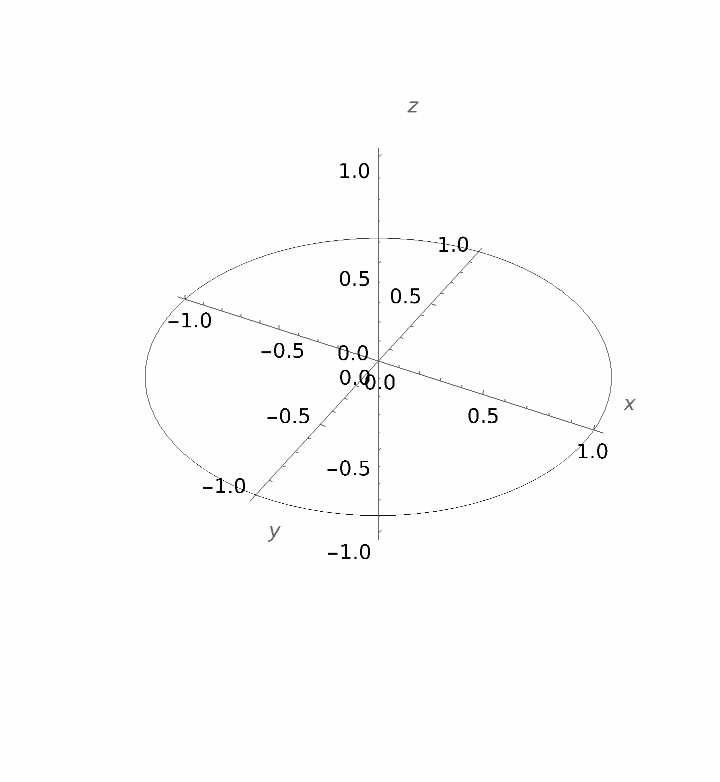

A 3D ellipse:

In[6]:=

Graphics3D[
ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{0, 0, 0}, {1, 3}, {{0, 1, 0}, {0, 0, 1}}],
Boxed -> False,
AxesOrigin -> {0, 0, 0},
Axes -> True,
AxesEdge -> {.5, .5, .5},
AxesLabel -> {x, y, z}
]

Out[6]=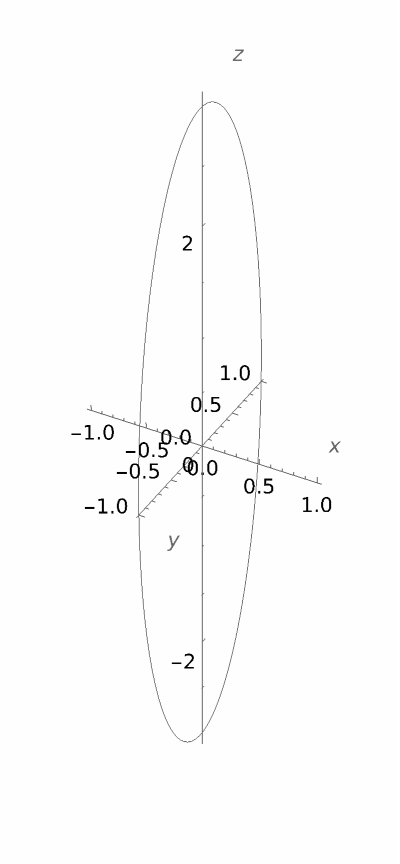

A 3D elliptical arc:

In[7]:=

Graphics3D[
ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{1, 1, 1}, {1, 3}, {{1, 0, 0}, {0, 0, 1}}, {0, Pi/2}],
Axes -> True,
AxesLabel -> {x, y, z}
]

Out[7]=

Scope (4)

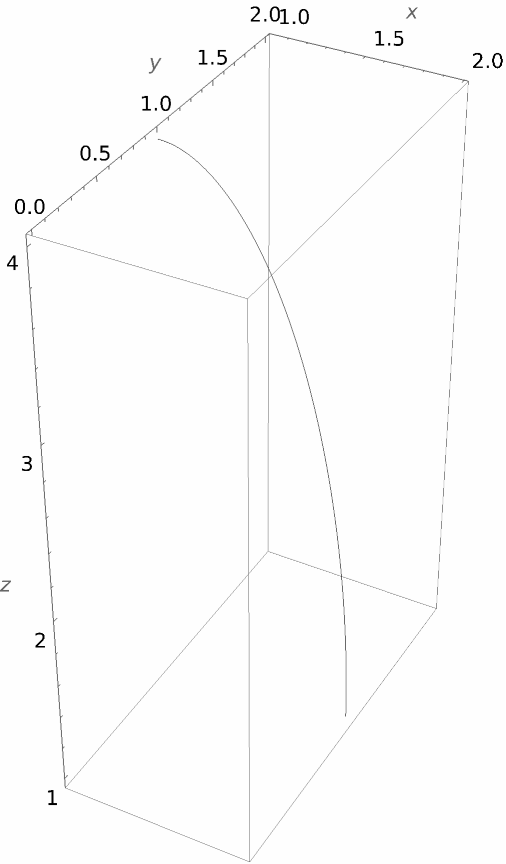Use SplineCircle as a FilledCurve specification:

In[8]:=

Graphics[FilledCurve[{
{ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{0, 0}, 2]},
{ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{1, 1}, 1]}
}]
]

Out[8]=

Use SplineCircle as a Tube curve specification:

In[9]:=

Out[9]=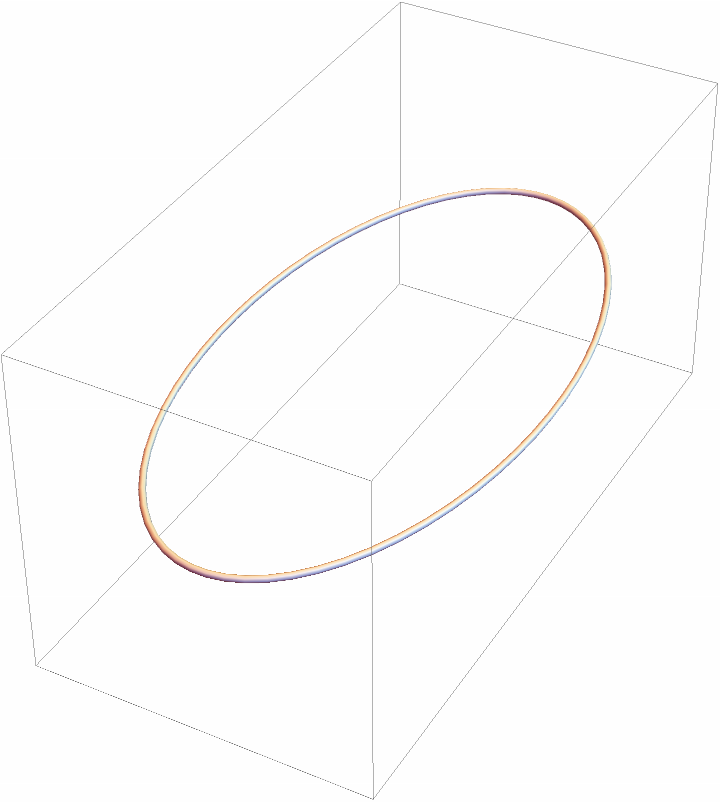

Use SplineCircle as an Arrow curve specification:

In[10]:=

SeedRandom[6]
points = RandomReal[1, {10, 3}];
axes = RandomReal[1, {10, 2, 3}];
angles = RandomReal[2 Pi, {10, 2}];
Graphics3D[
MapThread[
Arrow @* ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], {points, ConstantArray[1, 10], axes, angles}]]

Out[14]=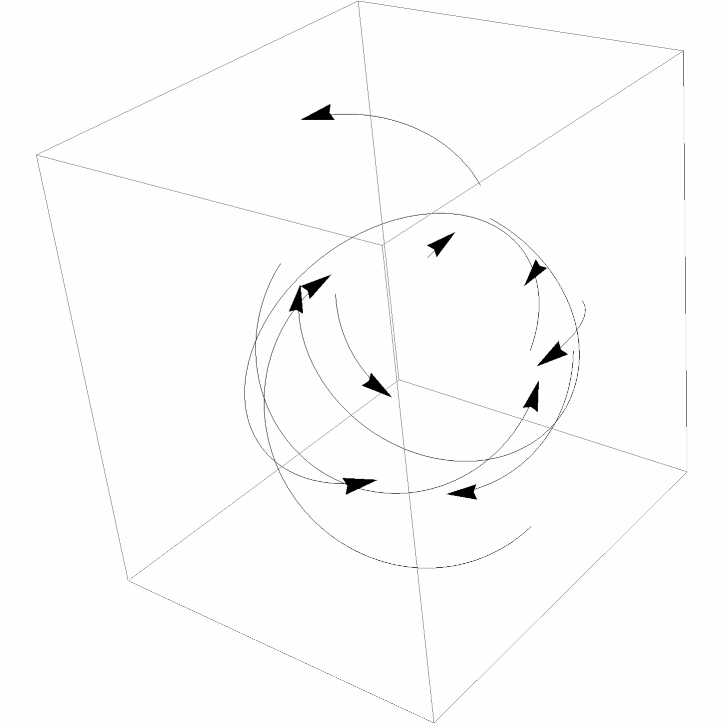

Rendering of a fairly large number of circle tubes:

In[15]:=

Out[15]=

Properties and Relations (2)

A 2D SplineCircle with a non-default semimajor axis is equivalent to a geometric transformation of a Circle object:

In[16]:=

Out[16]=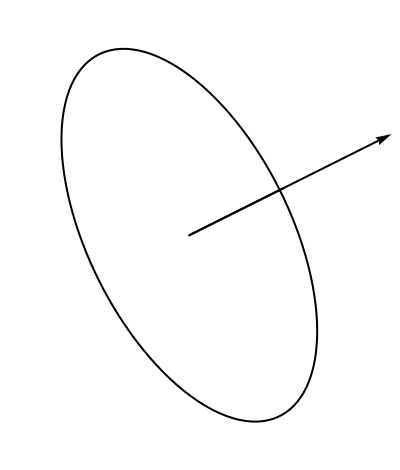

The Circle equivalent:

In[17]:=

Graphics[{Arrow[{{0, 0}, {2, 1}}], GeometricTransformation[Circle[{0, 0}, {1, 2}], RotationTransform[{{1, 0}, {2, 1}}, {0, 0}]]}, ImageSize -> 200]

Out[17]=

Possible Issues (3)

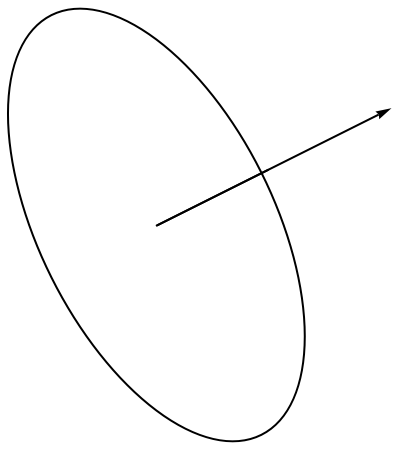When only a symmetry axis {x,y,z} is specified, the largest component of the symmetry axis is computed, and the third coordinate starting with the largest component in a RHS is determined. Then the semimajor axis is assumed to be perpendicular to both the third component and the symmetry axis. For example, suppose the symmetry axis is:

In[18]:=

The largest component is in the z direction, and so the third coordinate would be the y coordinate. Then the semimajor axis is assumed to be in the direction:

In[19]:=