Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a BSplineCurve primitive representing a circle
ResourceFunction["SplineCircle"][{x,y}, r] returns a BSplineCurve representation of a 2D circle with center {x,y} and radius r. | |
ResourceFunction["SplineCircle"][{x, y}, {r1,r2}] returns a 2D ellipse with semimajor axis r1 and semiminor axis r2, and with the semimajor axis in the x direction. | |
ResourceFunction["SplineCircle"][{x, y}, {r1,r2}, u] returns a 2D ellipse with the semimajor axis in the direction u. | |
ResourceFunction["SplineCircle"][{x, y}, {r1,r2}, u, {θ1, θ2}] returns a 2D elliptical arc from θ1 to θ2 measured from the semimajor axis. | |
ResourceFunction["SplineCircle"][{x, y, z}, r] returns a BSplineCurve representation of a 3D circle with center {x,y,z} and radius r, with the symmetry axis in the z direction. | |
ResourceFunction["SplineCircle"][{x, y, z},{r1,r2}] returns a 3D ellipse with semimajor axis r1 and semiminor axis r2, and with the semimajor axis in the x direction. | |
ResourceFunction["SplineCircle"][{x, y, z},{r1,r2}, a] returns a 3D ellipse with the symmetry axis in the direction a. | |
ResourceFunction["SplineCircle"][{x, y, z}, {r1,r2}, {u, v}] returns a 3D ellipse with the semimajor axis in the direction u, and with the elliptical plane being spanned by u and v. | |
ResourceFunction["SplineCircle"][{x, y, z},{r1,r2}, p, {θ1, θ2}] returns a 3D elliptical arc in the plane specified by p, where p can be the symmetry axis or the plane spanned by 3D vectors u and v. |
A 2D circle:
| In[1]:= |
| Out[1]= |  |
A 2D elliptical arc:
| In[2]:= |
| Out[2]= | 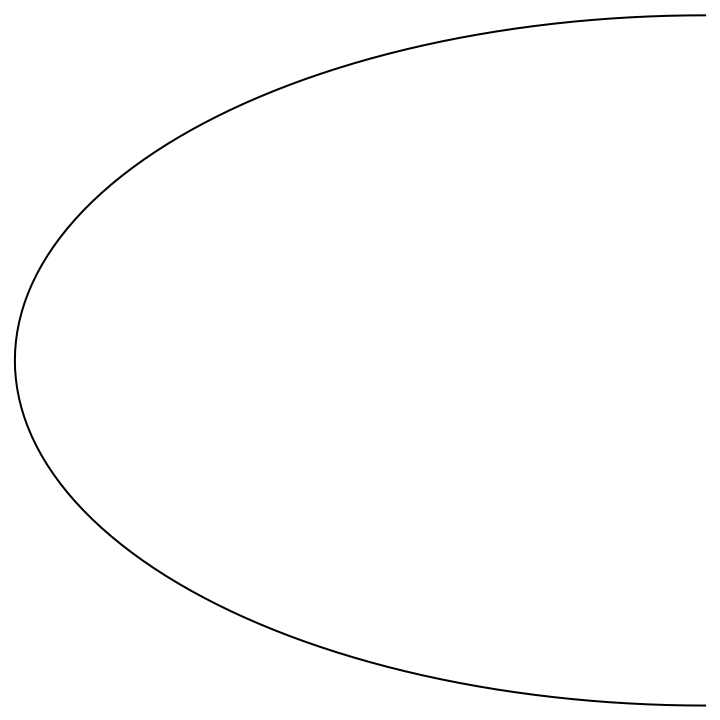 |
A 2D ellipse with semimajor axis in the direction {4, 1}:
| In[3]:= |
| Out[3]= | 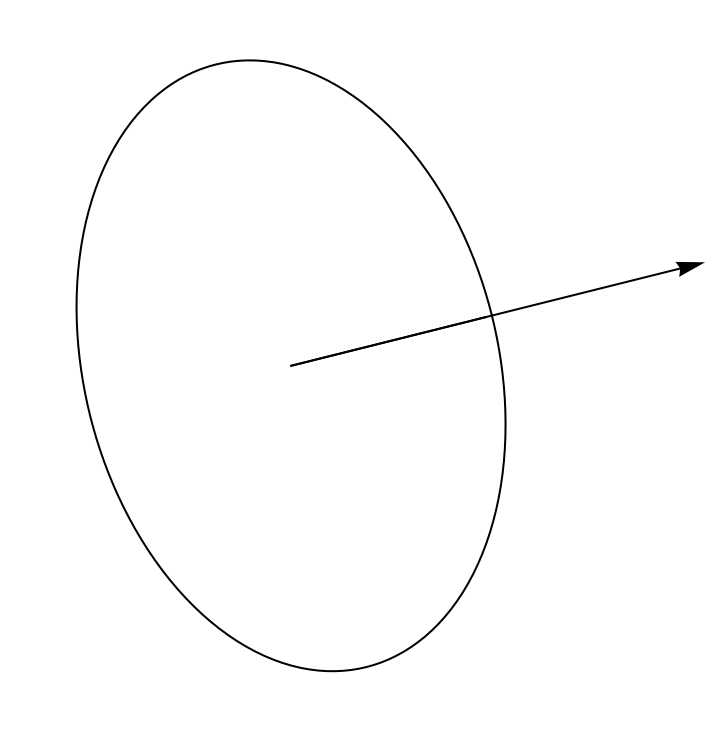 |
Differently styled ellipses:
| In[4]:= | ![Table[Graphics[{d, ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{0, 0}, {1, 2}]}], {d, {Red, Dashed, Thick, Directive[Blue, Thickness[.1], Dashed]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/d68/d68e4122-d684-41c5-9855-c3558aefe757/7b0fbb889ba7bddd.png) |
| Out[4]= | 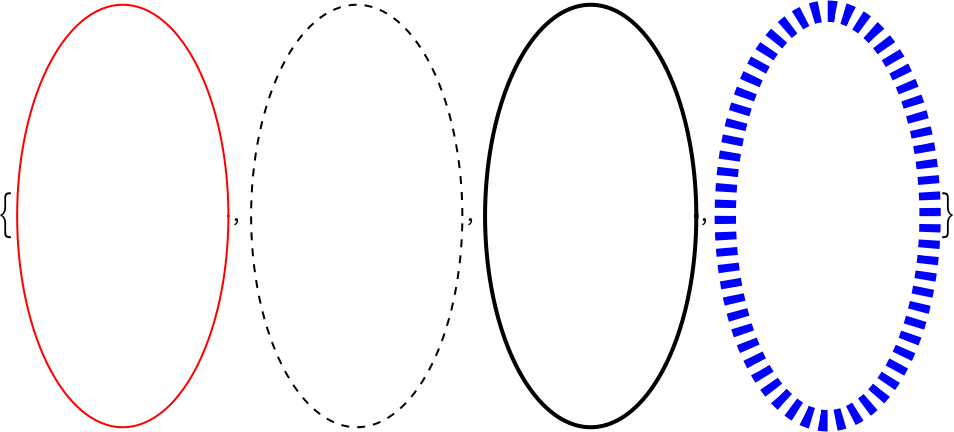 |
A 3D circle:
| In[5]:= | ![Graphics3D[
ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{0, 0, 0}, 1],
Boxed -> False,
Axes -> True,
AxesOrigin -> {0, 0, 0},
AxesEdge -> {.5, .5, .5},
AxesLabel -> {x, y, z}
]](https://www.wolframcloud.com/obj/resourcesystem/images/d68/d68e4122-d684-41c5-9855-c3558aefe757/110cc034e104b032.png) |
| Out[5]= | 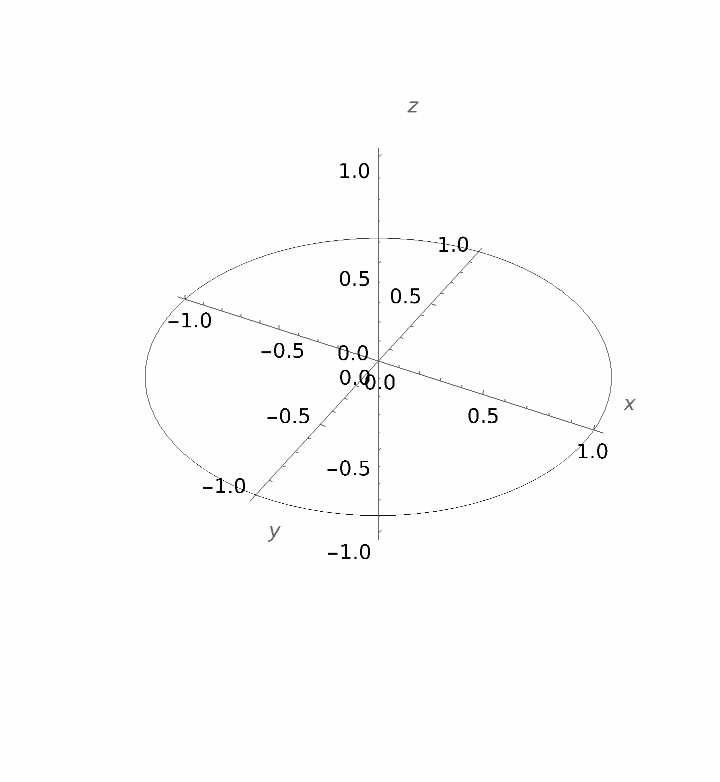 |
A 3D ellipse:
| In[6]:= | ![Graphics3D[
ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{0, 0, 0}, {1, 3}, {{0, 1, 0}, {0, 0, 1}}],
Boxed -> False,
AxesOrigin -> {0, 0, 0},
Axes -> True,
AxesEdge -> {.5, .5, .5},
AxesLabel -> {x, y, z}
]](https://www.wolframcloud.com/obj/resourcesystem/images/d68/d68e4122-d684-41c5-9855-c3558aefe757/0fd148825df6bd70.png) |
| Out[6]= | 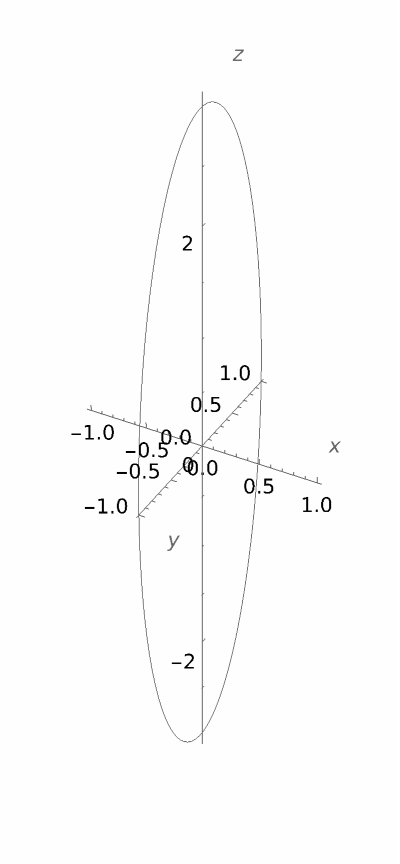 |
A 3D elliptical arc:
| In[7]:= | ![Graphics3D[
ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{1, 1, 1}, {1, 3}, {{1, 0, 0}, {0, 0, 1}}, {0, Pi/2}],
Axes -> True,
AxesLabel -> {x, y, z}
]](https://www.wolframcloud.com/obj/resourcesystem/images/d68/d68e4122-d684-41c5-9855-c3558aefe757/438ced08add97f11.png) |
| Out[7]= | 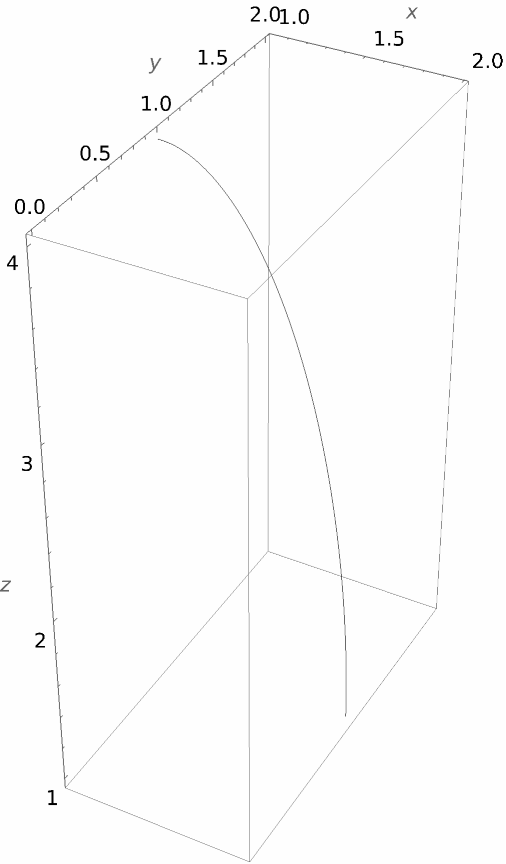 |
Use SplineCircle as a FilledCurve specification:
| In[8]:= | ![Graphics[FilledCurve[{
{ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{0, 0}, 2]},
{ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{1, 1}, 1]}
}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/d68/d68e4122-d684-41c5-9855-c3558aefe757/1fe94e73ad9cf500.png) |
| Out[8]= |  |
Use SplineCircle as a Tube curve specification:
| In[9]:= |
| Out[9]= | 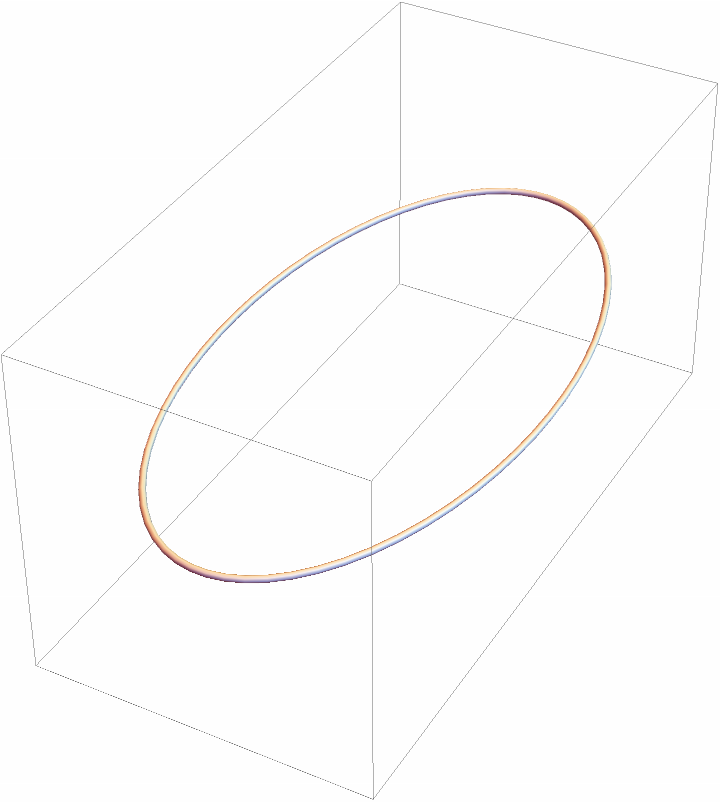 |
Use SplineCircle as an Arrow curve specification:
| In[10]:= | ![SeedRandom[6]
points = RandomReal[1, {10, 3}];
axes = RandomReal[1, {10, 2, 3}];
angles = RandomReal[2 Pi, {10, 2}];
Graphics3D[
MapThread[
Arrow @* ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], {points, ConstantArray[1, 10], axes, angles}]]](https://www.wolframcloud.com/obj/resourcesystem/images/d68/d68e4122-d684-41c5-9855-c3558aefe757/370bda950492548a.png) |
| Out[14]= | 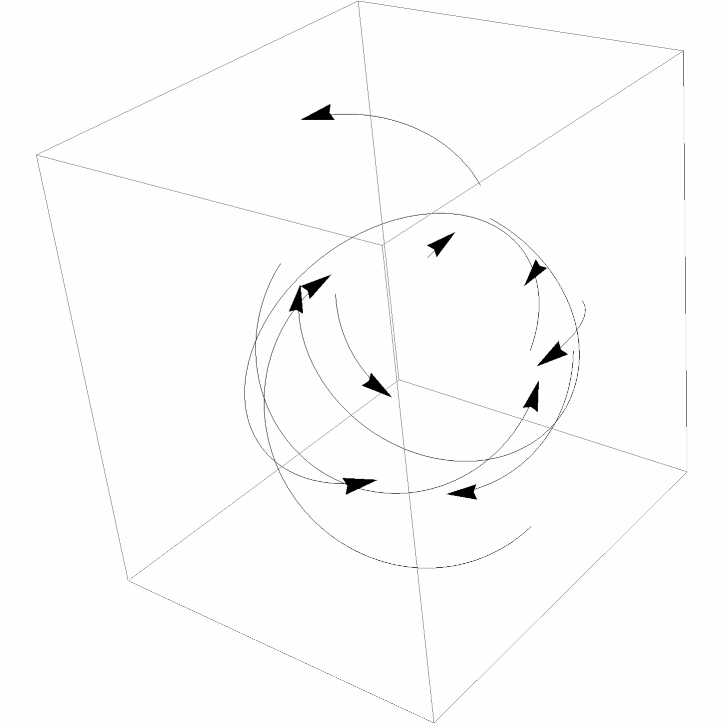 |
Rendering of a fairly large number of circle tubes:
| In[15]:= | ![Graphics3D[
MapThread[
Tube@*ResourceFunction[
"SplineCircle", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], {RandomReal[3, {300, 3}], RandomReal[{2, 3}, 300], RandomReal[1, {300, 2, 3}]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/d68/d68e4122-d684-41c5-9855-c3558aefe757/673fd2002de2041a.png) |
| Out[15]= |  |
A 2D SplineCircle with a non-default semimajor axis is equivalent to a geometric transformation of a Circle object:
| In[16]:= |
| Out[16]= | 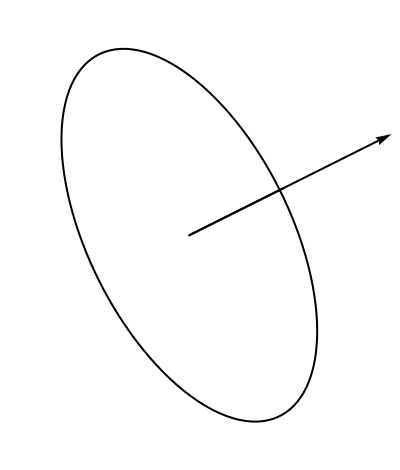 |
The Circle equivalent:
| In[17]:= | ![Graphics[{Arrow[{{0, 0}, {2, 1}}], GeometricTransformation[Circle[{0, 0}, {1, 2}], RotationTransform[{{1, 0}, {2, 1}}, {0, 0}]]}, ImageSize -> 200]](https://www.wolframcloud.com/obj/resourcesystem/images/d68/d68e4122-d684-41c5-9855-c3558aefe757/474e54da8447f8ac.png) |
| Out[17]= | 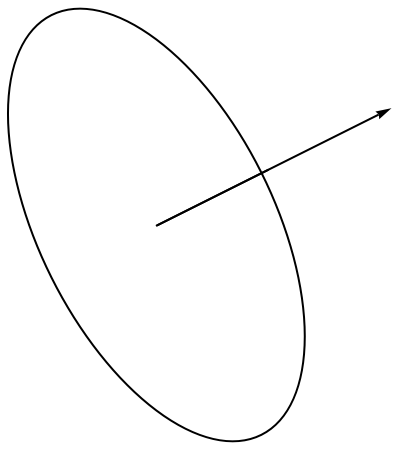 |
When only a symmetry axis {x,y,z} is specified, the largest component of the symmetry axis is computed, and the third coordinate starting with the largest component in a RHS is determined. Then the semimajor axis is assumed to be perpendicular to both the third component and the symmetry axis. For example, suppose the symmetry axis is:
| In[18]:= |
The largest component is in the z direction, and so the third coordinate would be the y coordinate. Then the semimajor axis is assumed to be in the direction:
| In[19]:= |
| Out[19]= |
Check:
| In[20]:= |
| Out[20]= | 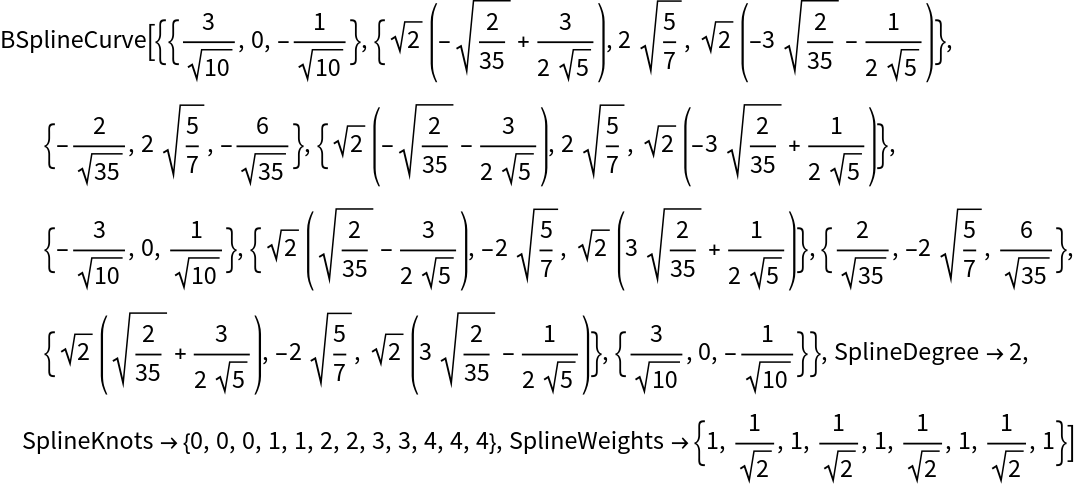 |
This work is licensed under a Creative Commons Attribution 4.0 International License