Basic Examples (2) 

A spherical triangle:

In[1]:=

Show the spherical triangle:

In[2]:=

Out[2]=

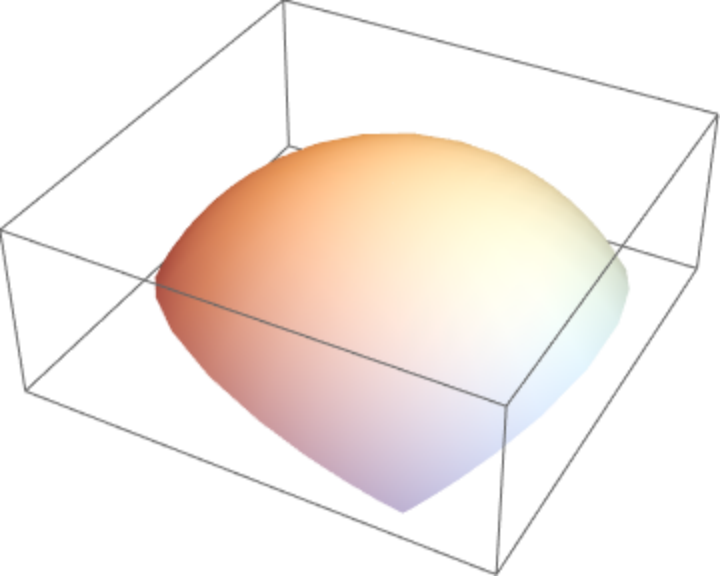
A spherical rectangle:

In[3]:=

Show the spherical rectangle:

In[4]:=

Out[4]=

Scope (2) 

A spherical polygon with a specified sphere center:

In[5]:=

Show the polygon on a sphere:

In[6]:=

Out[6]=

Use directives to specify the face colors:

In[7]:=

Out[7]=

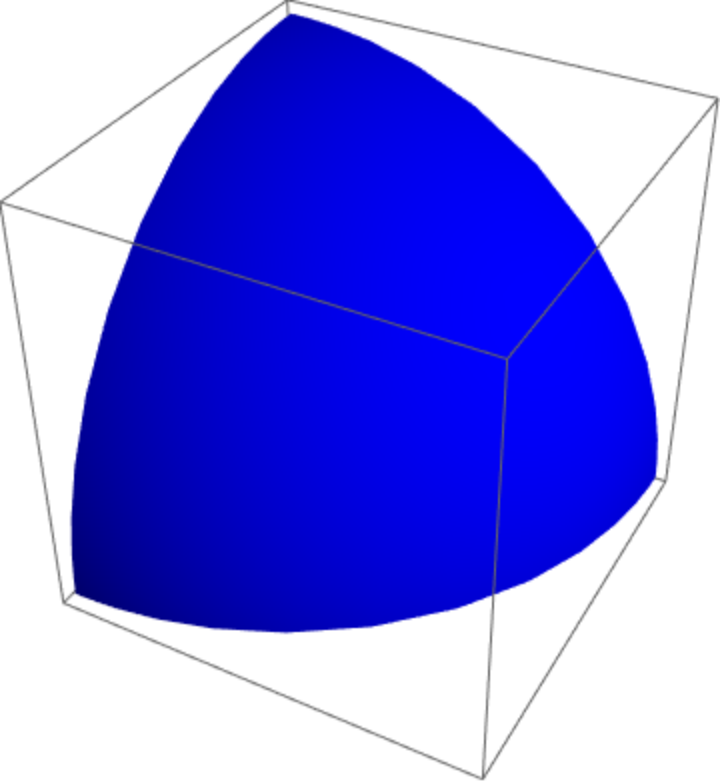
In[8]:=

Out[8]=

Options (3) 

EdgeStyle (2) 

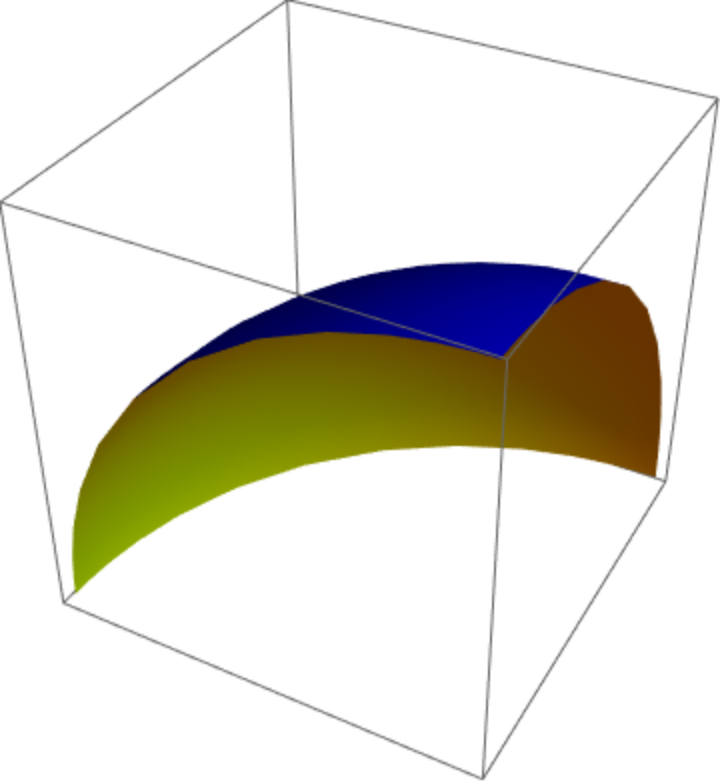
Specify the style of the edges:

In[9]:=

Out[9]=

---

Specify face and edge styling:

In[10]:=

Out[10]=

ShowEdges (1) 

Show the edges of the spherical polygon:

In[11]:=

Out[11]=

Properties and Relations (1) 

SphericalPolygon returns a GraphicsComplex object:

In[12]:=

Out[12]=

Possible Issues (3) 

Consecutive vertices of SphericalPolygon cannot be antipodal points:

In[13]:=

Out[13]=

SphericalPolygon does not directly support spherical digons:

In[14]:=

Out[14]=

To render a spherical digon, add the midpoints of the edges:

In[15]:=

Out[15]=

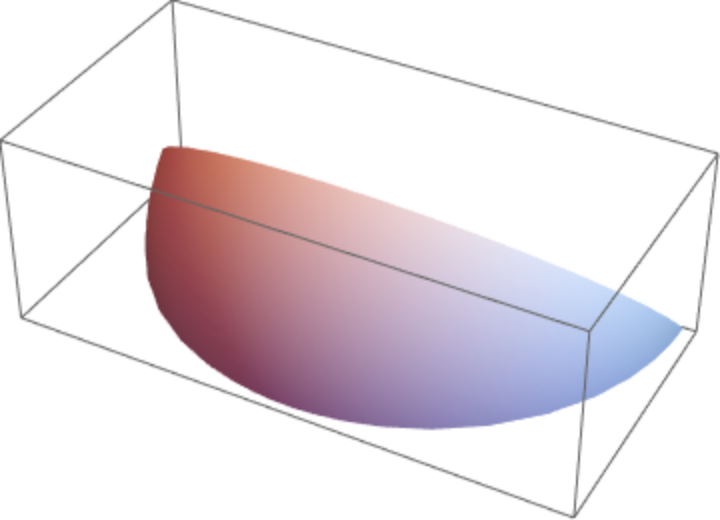
SphericalPolygon is best used for convex spherical polygons. Concave polygons might display artifacts:

In[16]:=

Out[16]=

Split the concave spherical polygon into two spherical triangles:

In[17]:=

Out[17]=

Neat Examples (2) 

Random triangulation of a sphere:

In[18]:=

In[19]:=

Out[19]=

Use SphericalPolygon to depict a soccer ball:

In[20]:=

In[21]:=

Out[21]=