Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SphericalLinearInterpolation

Source Notebook

Evaluate the piecewise spherical linear interpolant of given data

Contributed by: Jan Mangaldan

ResourceFunction["SphericalLinearInterpolation"][data,t]

finds a piecewise spherical linear interpolation of data at the point t.

ResourceFunction["SphericalLinearInterpolation"][data]

represents an operator form of ResourceFunction["SphericalLinearInterpolation"] that can be applied to an expression.

Details

Spherical linear interpolation is also known as "slerp".
ResourceFunction["SphericalLinearInterpolation"][data,t] evaluates so as to agree with data at every point explicitly specified in data.
data should be in the form {{t1,v1},{t2,v2},…}, where the ti must be real numbers, and the vi must be vectors on a sphere, all of the same dimension.

Examples

Basic Examples (3) 

Generate some data over a sphere of radius 3:

In[1]:=
vecs = 3 (Normalize /@ RandomVariate[NormalDistribution[], {5, 3}]); vals = FoldList[Plus, 0, Normalize[VectorAngle @@@ Partition[vecs, 2, 1], Total]]; data = Transpose[{vals, vecs}]
Out[1]=

Evaluate the piecewise spherical linear interpolant of the data at a given value:

In[2]:=
ResourceFunction["SphericalLinearInterpolation"][data, 0.7]
Out[2]=

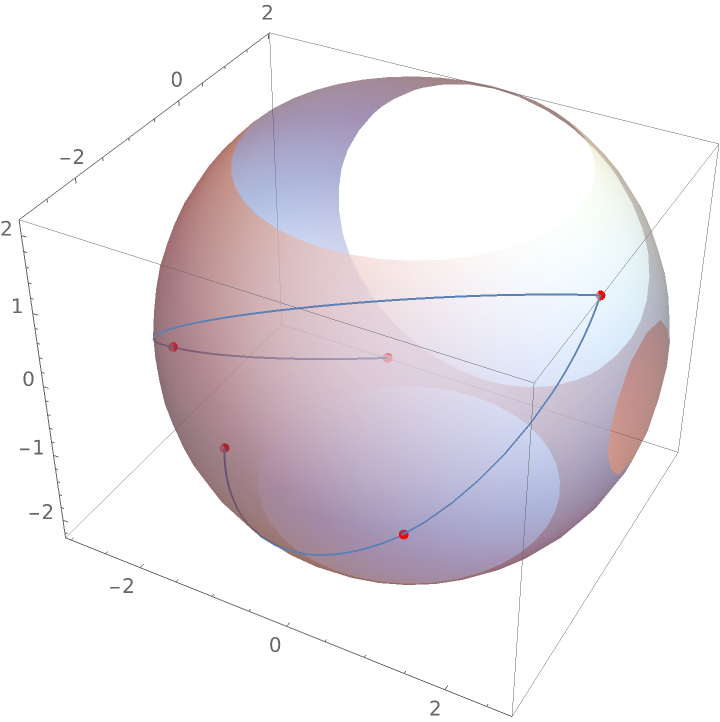
Plot the piecewise spherical linear interpolant along with the original data:

In[3]:=
Show[ParametricPlot3D[ ResourceFunction["SphericalLinearInterpolation"][data, t], {t, 0, 1}], Graphics3D[{{Opacity[0.6], Sphere[{0, 0, 0}, 3]}, {Red, AbsolutePointSize[5], Point[vecs]}}]]
Out[3]=

Scope (2) 

Evaluate the piecewise spherical linear interpolant for four-dimensional vectors:

In[4]:=
data = Transpose[{N[Subdivide[4]], Normalize /@ RandomVariate[NormalDistribution[], {5, 4}]}]; ResourceFunction["SphericalLinearInterpolation"][data, 0.354]
Out[4]=

Evaluate the piecewise spherical linear interpolant for high-precision data:

In[5]:=
data = Transpose[{N[Subdivide[4], 20], Normalize /@ RandomVariate[NormalDistribution[], {5, 3}, WorkingPrecision -> 20]}]; ResourceFunction["SphericalLinearInterpolation"][data, 1/2]
Out[5]=

Applications (2) 

A function for taking a bounded random step on a sphere:

In[6]:=
boundedRandomStep[v_?VectorQ, \[CurlyPhi]_?NumericQ] := RotationMatrix[{{0, 0, 1}, v}].({0, 0, Cos[\[CurlyPhi]]} + Sin[\[CurlyPhi]] Append[ Normalize[RandomVariate[NormalDistribution[], 2]], 0])

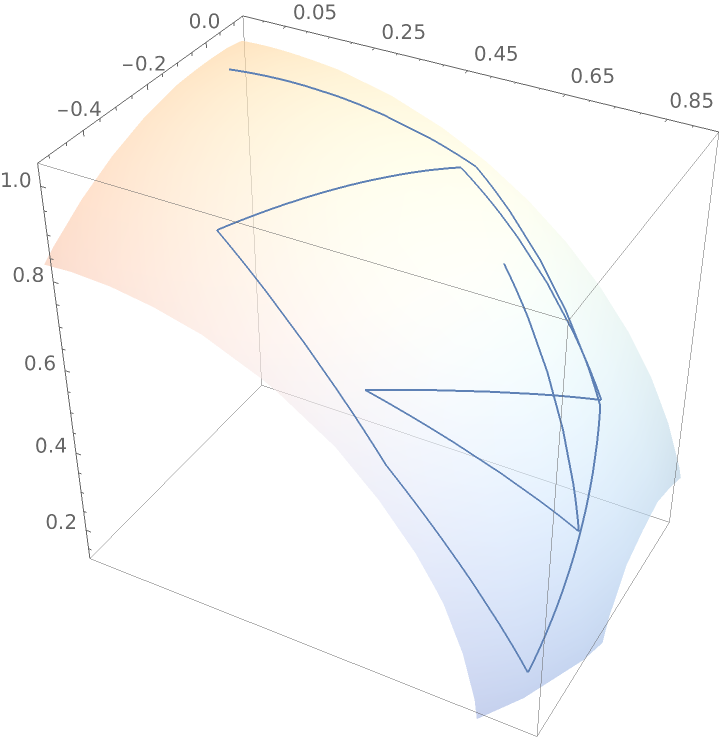
Visualize a random walk with bounded steps on a sphere:

In[7]:=
steps = NestList[boundedRandomStep[#, \[Pi]/6] &, {0, 0, 1}, 10]; vals = FoldList[Plus, 0, Normalize[VectorAngle @@@ Partition[steps, 2, 1], Total]]; data = Transpose[{vals, steps}]; Show[ParametricPlot3D[ ResourceFunction["SphericalLinearInterpolation"][data, t], {t, 0, 1}], Graphics3D[{Opacity[0.6], Sphere[]}]]
Out[7]=

Version History

  • 1.0.0 – 11 January 2021

Source Metadata

  • Citation:
    • Kahan W., How Futile are Mindless Assessments of Roundoff in Floating-Point Computation?
      Available online http://people.eecs.berkeley.edu/~wkahan/Mindless.pdf
    • Shoemake K., Animating rotation with quaternion curves. In Proceedings of the 12th annual conference on Computer graphics and interactive techniques (SIGGRAPH ‘85). Association for Computing Machinery, New York, USA, 245–254.
      DOI: 10.1145/325334.325242

Related Resources

Author Notes

In the compiled part of the implementation, I use Kahan's formula for the vector angle for a numerically stable evaluation.

License Information