Function Repository Resource:

SphericalCurve

Get curves defined over a sphere

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["SphericalCurve"][{par₁,par₂,…},"type"]

gives the parametrization of a curve of the given type on a sphere, with parameters par_i.

Details and Options

A spherical curve is a curve traced on a sphere.

Types of curves are "Clelia", "HyperbolicTangentSpiral", "SatelliteCurve", "SeiffertsSphericalSpiral", "SphereRhumbLine", "SphericalCardioid", "SphericalCycloid", "SphericalEllipse", "SphericalHelix", "SphericalHelix", "SphericalLissajous", "SphericalLoxodrome", "SphericalLoxodromeUnitSpeed", "SphericalNephroid", "SphericalPendulum", "SphericalSinusoid", "SphericalTrochoid", "SpheroCylindricalCurve", "SpinningTop" and "TennisBallSeam".

Examples

Basic Examples (2)

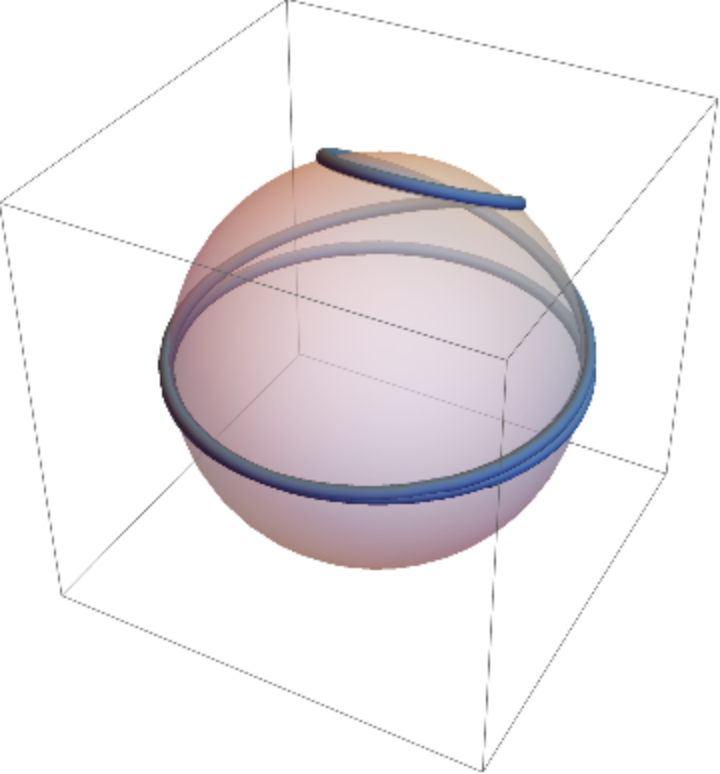
Get the expression for a hyperbolic tangent spiral on a sphere:

In[1]:=

Out[1]=

Plot it:

In[2]:=

Show[ParametricPlot3D[Evaluate[hts],
{t, -10, 10}, Axes -> None, PlotStyle -> Tube[.035]], Graphics3D[{Opacity[.5], Sphere[{0, 0, 0}, .99]}], PlotRange -> All]

Out[2]=

Scope (13)

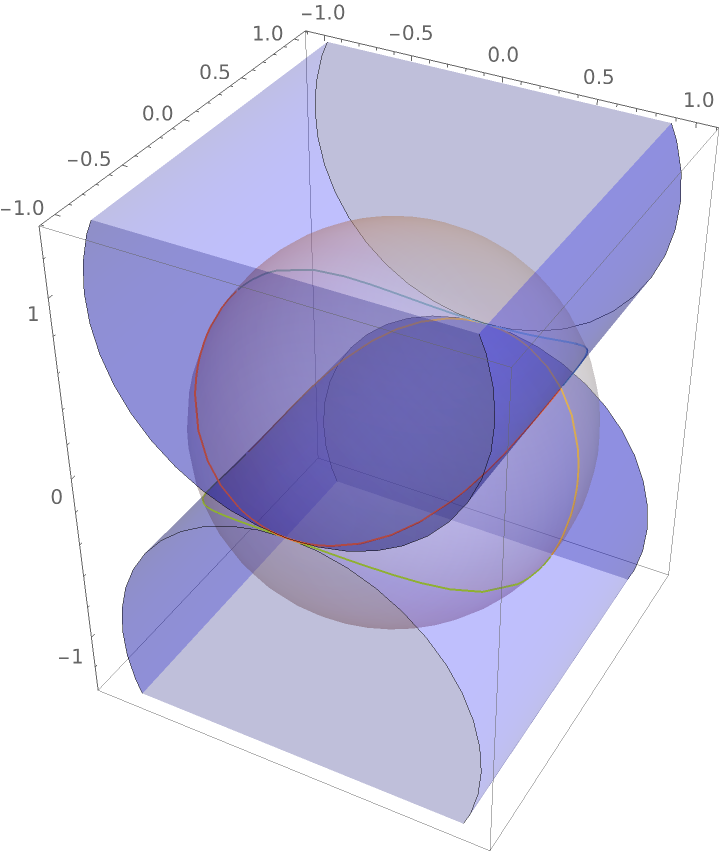
A sphero-cylindrical curve is the intersections between a sphere and a cylinder of revolution:

In[3]:=

$Show[ParametricPlot3D[ Evaluate[{ResourceFunction["SphericalCurve"][{1, -1, 1}, t, "SpheroCylindricalCurve"], ResourceFunction["SphericalCurve"][{1, -1, -1}, t, "SpheroCylindricalCurves"], -ResourceFunction[ "SphericalCurve"][{1, -1, 1}, t, "SpheroCylindricalCurves"], -ResourceFunction[ "SphericalCurve"][{1, -1, -1}, t, "SpheroCylindricalCurves"]}], {t, -\[Pi], \[Pi]}, Axes -> True], Graphics3D[{Opacity[.25], Sphere[{0, 0, 0}, 1], Blue, Cylinder[{{0, 1, 1}, {0, -1., 1}}], Cylinder[{{0, 1, -1}, {0, -1., -1}}]}]]$

Out[3]=

Seiffert's spherical spiral:

In[4]:=

Out[4]=

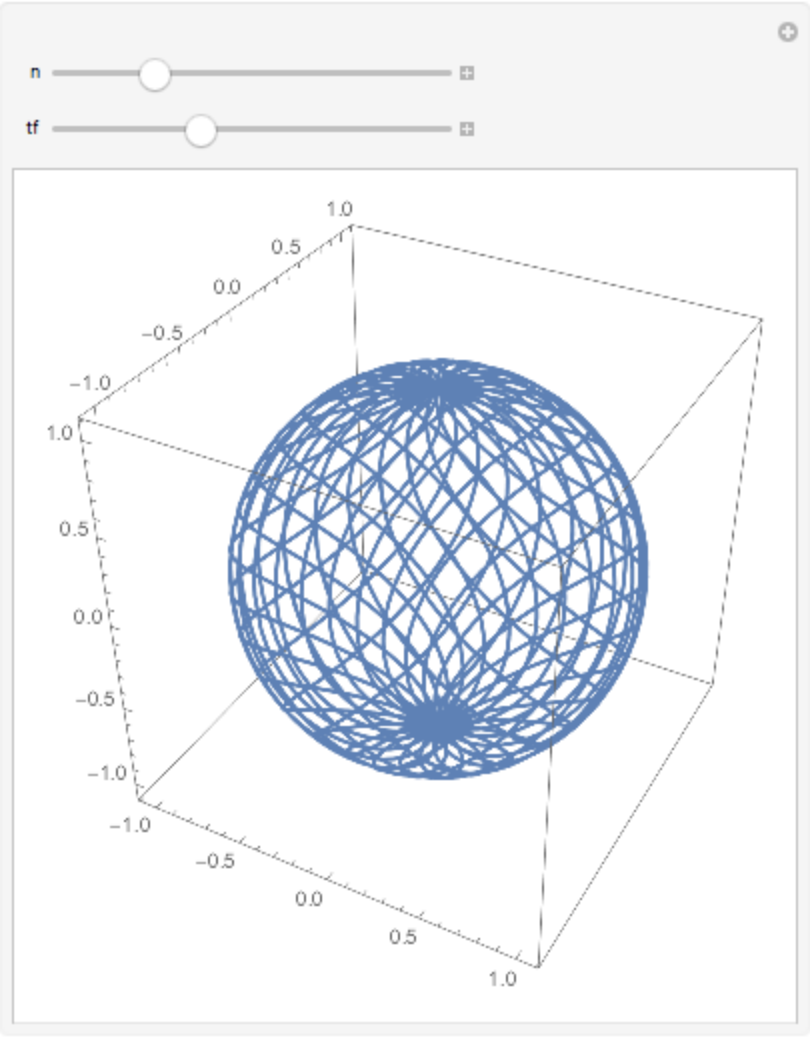
The Clelia:

In[5]:=

Out[5]=

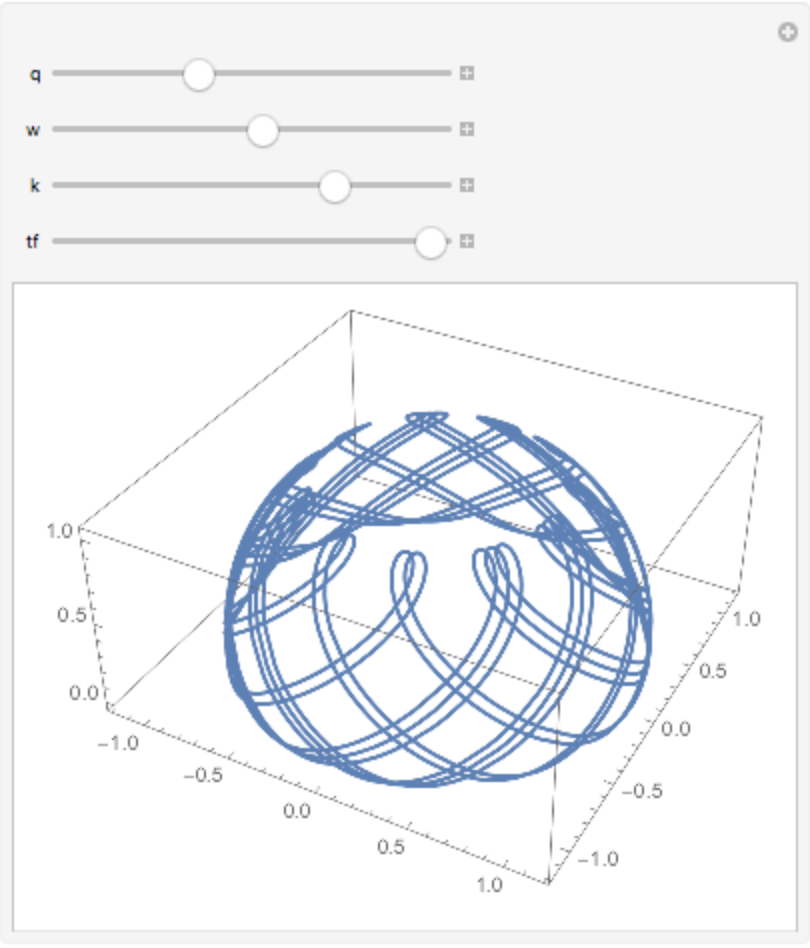
Spherical cycloid:

In[6]:=

$Manipulate[ ParametricPlot3D[ Evaluate[ResourceFunction["SphericalCurve"][{1, q, w, k}, t, "SphericalCycloid"]], {t, 0, tf}, Axes -> True, PlotRange -> All], {{q, 1.1}, 0, \[Pi]}, {{w, .532}, 0, 1}, {{k, .734}, 0, 1}, {{tf, 250}, 1, 250}]$

Out[6]=

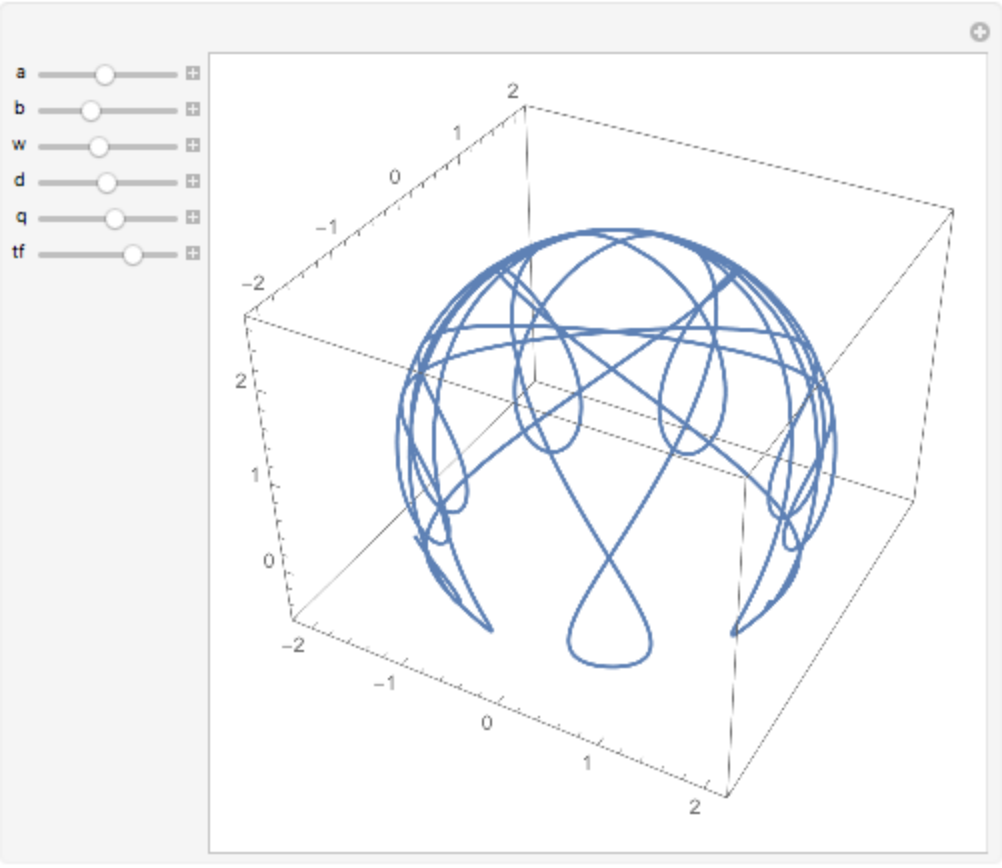
Spherical trochoid:

In[7]:=

$Manipulate[ParametricPlot3D[ Evaluate[ ResourceFunction["SphericalCurve"][{a, b, w, d, q}, t, "SphericalTrochoid"]], {t, 0, tf}, Axes -> True, PlotRange -> All], {{a, 1.5}, 0, \[Pi], ImageSize -> Tiny}, {{b, 1.1}, 0, \[Pi], ImageSize -> Tiny}, {{w, 1.31}, 0, \[Pi], ImageSize -> Tiny}, {{d, 1.55}, 0, \[Pi], ImageSize -> Tiny}, {{q, 1.77}, 0, \[Pi], ImageSize -> Tiny}, {{tf, 36}, 1, 50, ImageSize -> Tiny}, ControlPlacement -> Left]$

Out[7]=

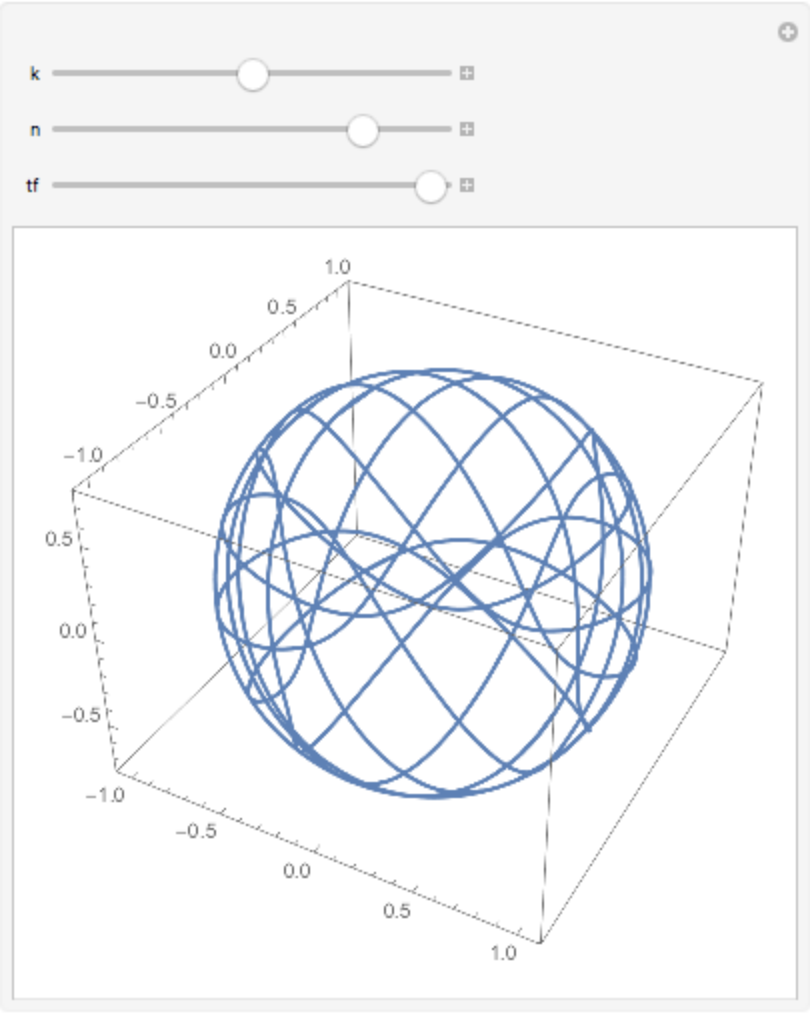
Spherical sinusoid:

In[8]:=

Out[8]=

Spherical ellipses:

In[9]:=

$Show[ParametricPlot3D[ Evaluate[Table[ ResourceFunction["SphericalCurve"][{4, 3, c, 1}, t, "SphericalEllipse"], {c, 1, 10, 1}]], {t, 0, 4 \[Pi]}, Axes -> None], Graphics3D[{Opacity[.5], Sphere[{0, 0, 0}, 3.99]}], PlotRange -> All]$

Out[9]=

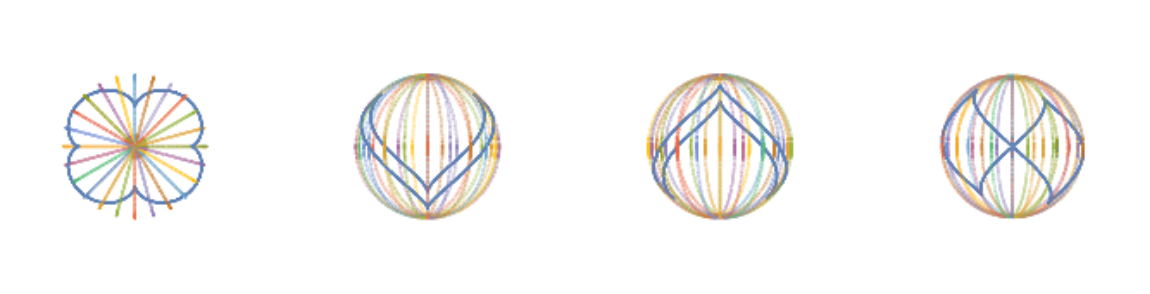
Spherical helix:

In[10]:=

$meridians[gl_] := ParametricPlot3D[ Evaluate[Table[ 1 {Cos[u] Cos[v], Sin[u] Cos[v], Sin[v]}, {u, 0, 2 \[Pi], gl}]], {v, -(\[Pi]/2), \[Pi]/2}, PlotStyle -> Opacity[.25]]$

In[11]:=

$With[{m = meridians[2 \[Pi]/24]}, GraphicsRow[ Show[ParametricPlot3D[ Evaluate[ ResourceFunction["SphericalCurve"][{2/3, 1/6}, t, "SphericalHelix"]], {t, 0, 2 \[Pi]}, Axes -> None, Boxed -> False, ViewPoint -> #], m] & /@ {Above, Front, Left, {Left, Front}}, ImageSize -> Full]]$

Out[11]=

Spherical cardioid:

In[12]:=

$Show[ParametricPlot3D[ Evaluate[ResourceFunction["SphericalCurve"][{1}, t, "SphericalCardioid"]], {t, 0, 4 \[Pi]}, Axes -> None], Graphics3D[{Opacity[.5], Sphere[{0, 0, 0}, 2.99]}]]$

Out[12]=

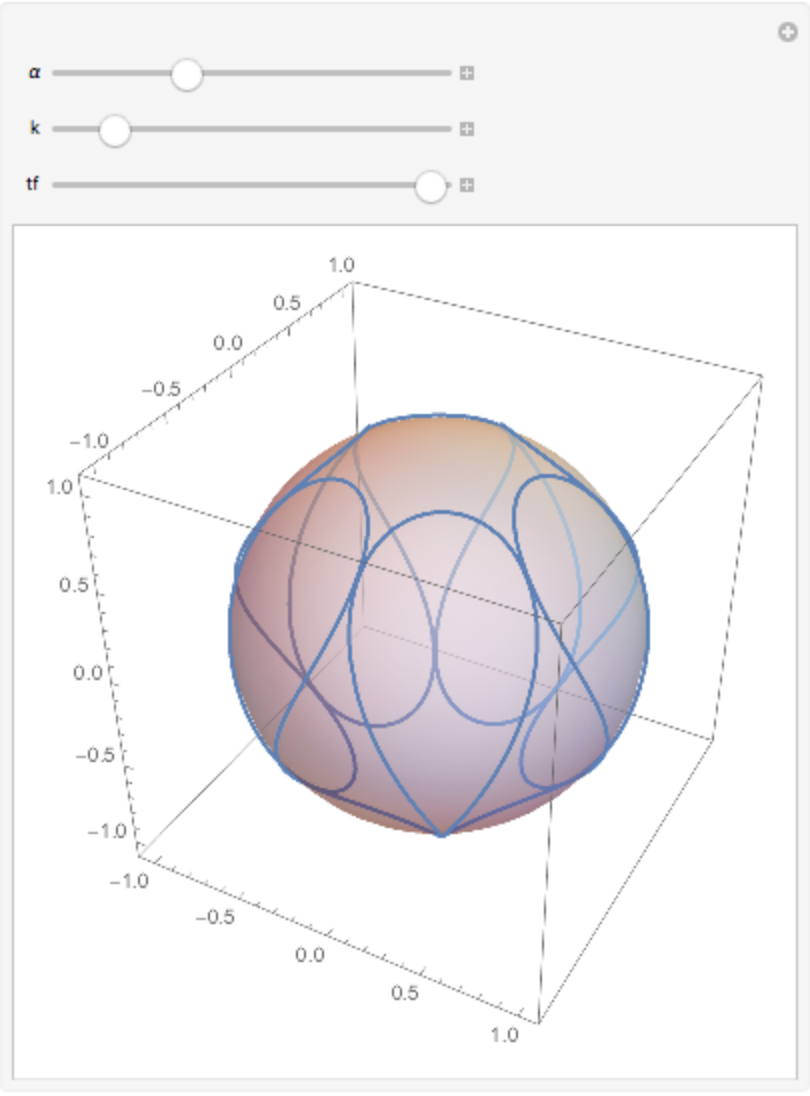
Satellite curve (Clelias and the spherical helices are special cases):

In[13]:=

$Manipulate[ Show[ParametricPlot3D[ Evaluate[ ResourceFunction["SphericalCurve"][{1, k, \[Alpha]}, t, "SatelliteCurve"]], {t, 0, tf}, Axes -> True, PlotRange -> All], Graphics3D[{Opacity[.5], Sphere[{0, 0, 0}, .99]}]], {{\[Alpha], 3 \[Pi]/4}, 0, 2 \[Pi]}, {{k, 3}, 0, 10}, {{tf, 4 \[Pi]}, 1, 50}]$

Out[13]=

Spherical pendulum:

In[14]:=

$sp = ResourceFunction[ "SphericalCurve"][{1(*longitude*), 1(*mass*), 1.57(*initial angle \[Theta]*), 0(*initial velocity \[Theta]*), 0(*initial angle \[CurlyPhi]*), 2(*angular momentum \[CurlyPhi]*)}, 30, "SphericalPendulum"]$

Out[14]=

Plot the curve:

In[15]:=

Out[15]=

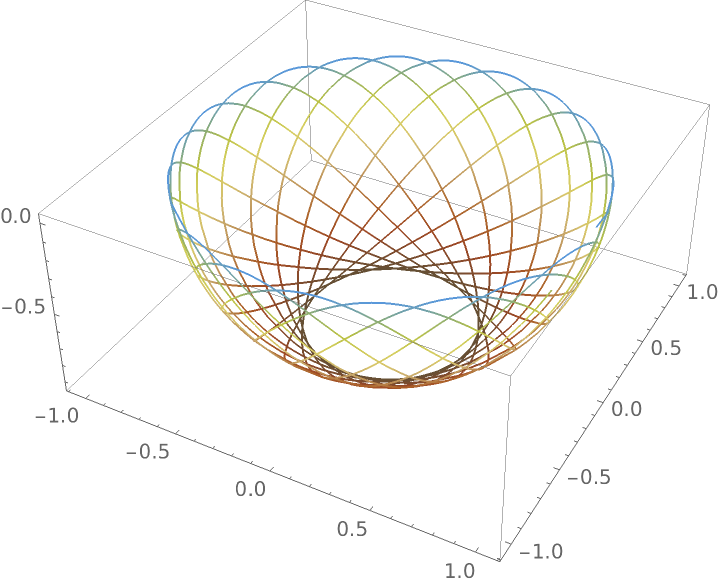
Stationary precession of a spinning top:

In[16]:=

Show[ResourceFunction[
"SphericalCurve"][{30(*initial nutation angle*), 10(*g*), 1(*transversal I*), 1(*initial spin*), 1(*longitudinal J*), .25(*height of center of mass*), .5(*mass*), 0.5(*initial nutation velocity*)}, 35, "SpinningTop"], Graphics3D[{Opacity[.5], Sphere[{0, 0, 0}, .45]}]]

Out[16]=

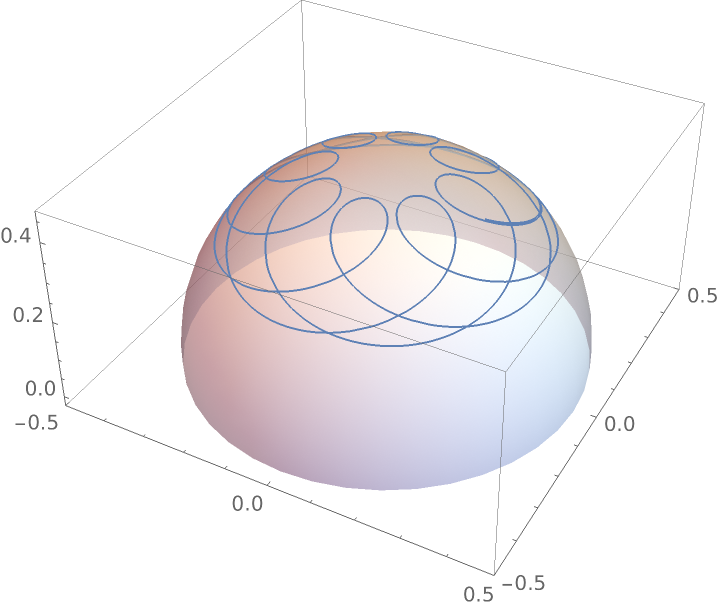
Spherical rhumb line:

In[17]:=

Out[17]=

In[18]:=

Out[18]=

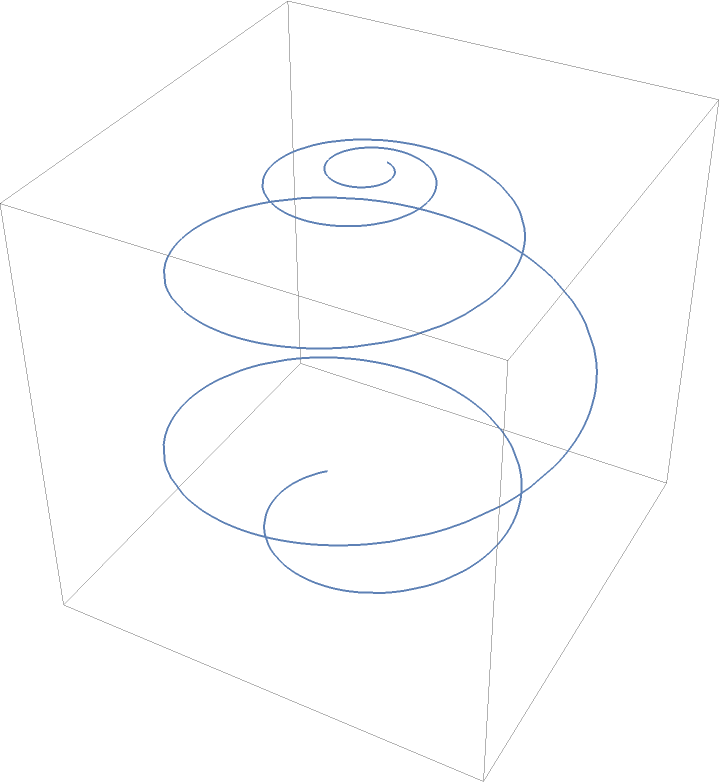
Spherical loxodrome:

In[19]:=

Out[19]=

Comparing with the unit–speed spherical loxodrome:

In[20]:=

ParametricPlot3D[
Evaluate[ResourceFunction["SphericalCurve"][{1, 1, .15}, t, #]],
{t, -10, 20}, Axes -> None, BoxRatios -> {1, 1, 1}] & /@ {"SphericalLoxodrome", "SphericalLoxodromeUnitSpeed"}

Out[20]=

Properties and Relations (3)

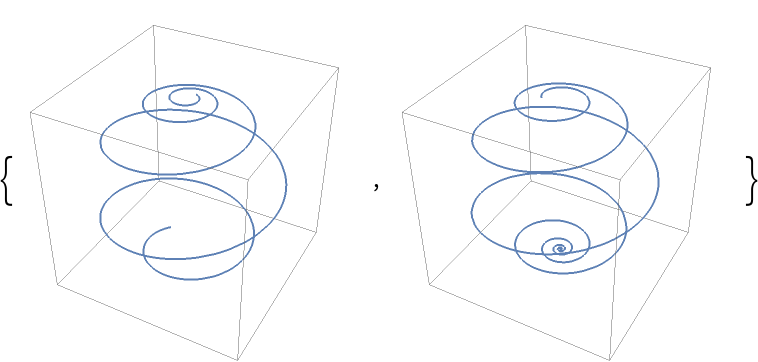
Compute quantities like ArcLength:

In[21]:=

Out[21]=

Compute the curvature:

In[22]:=

Out[22]=

The torsion:

In[23]:=

Out[23]=

Applications (4)

The spherical nephroid:

In[24]:=

The Frenet–Serret system of the curve:

In[25]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/ba1ea694-b2c2-43fe-a1b8-1e1d56073d9f"]

Out[25]=

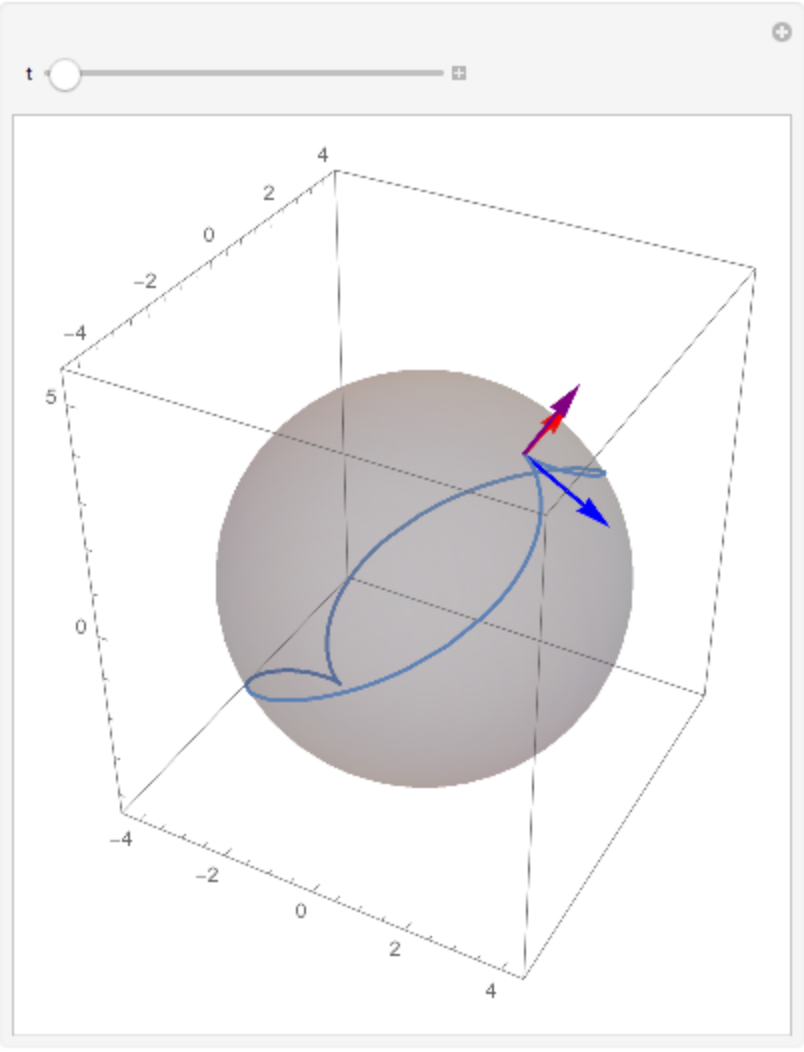
Plot the Frenet–Serret system:

In[26]:=

${tangent, normal, binormal} = Map[Arrow[{sn, sn + 2 #}] &, basis] // PowerExpand // FullSimplify; plot = ParametricPlot3D[Evaluate[sn], {t, 0, 2 \[Pi]}]; Manipulate[ Evaluate[Show[plot, Graphics3D[{Thick, Blue, tangent, Red, normal, Purple, binormal, Gray, Opacity[0.25], Sphere[{0, 0, 0}, 4]}], PlotRange -> All]], {t, 0, 2 \[Pi]}]$

Out[26]=

The seam line of a tennis ball:

In[27]:=

$Show[ParametricPlot3D[ ResourceFunction["SphericalCurve"][{2, 2, 2, 1}, t, "TennisBallSeam"], {t, 0, 2 \[Pi]}, Axes -> None, PlotPoints -> 150, PlotStyle -> {{White, Thickness[.01]}}], Graphics3D[{Opacity[.5], LightGreen, Sphere[]}]]$

Out[27]=

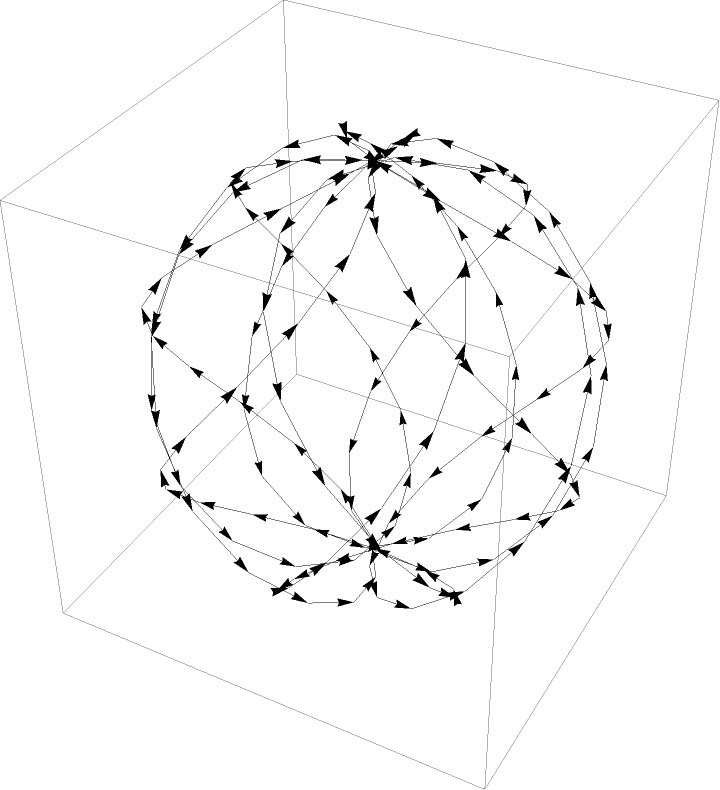
Spherical Lissajous:

In[28]:=

$Graphics3D[{Arrowheads[.02], ResourceFunction["ApproximatedCurve"][ ResourceFunction["SphericalCurve"][{3, 5, 7}, t, "SphericalLissajous"], {t, 0, 2 \[Pi], 150}, "Arrow"]}]$

Out[28]=

Distinct types of surfaces (like ruled surfaces) can be constructed from curves (used in fields like architecture):

In[29]:=

$ParametricPlot3D[ Evaluate[ResourceFunction["NormalSurface"][ ResourceFunction["SphericalCurve"][{3, 7, 5}, t, "SphericalSpiral"], t, {u, v}]], {u, 0, \[Pi]}, {v, 0, \[Pi]}, PlotPoints -> 60, Axes -> None]$

Out[29]=

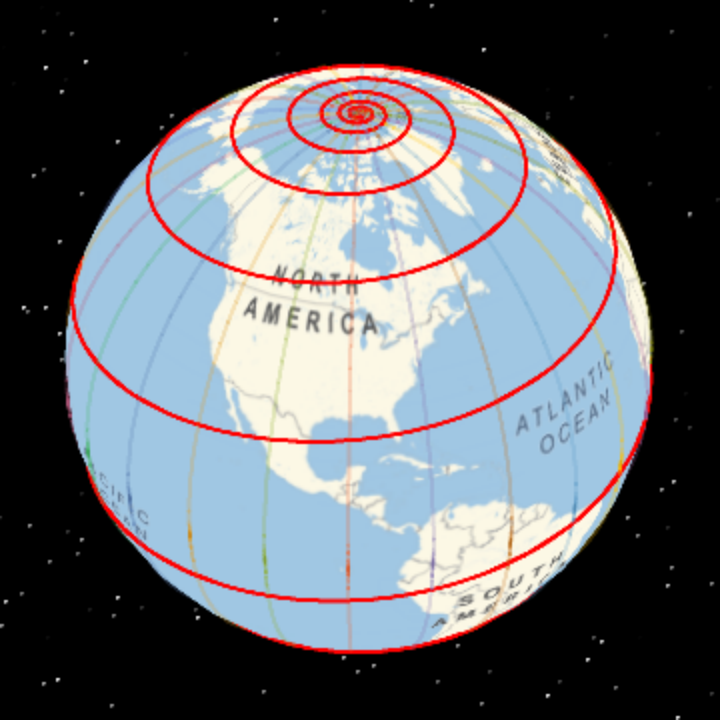
Meridians and loxodrome:

In[30]:=

$meridians[gl_] := ParametricPlot3D[ Evaluate[Table[{Cos[u] Cos[v], Sin[u] Cos[v], Sin[v]}, {u, 0, 2 \[Pi], gl}]], {v, -(\[Pi]/2), \[Pi]/2}, PlotStyle -> Opacity[.25]]$

In[31]:=

$Show[ResourceFunction["GeoGlobe3D"][], ParametricPlot3D[ Evaluate[ResourceFunction["SphericalCurve"][{1, 1, .1}, t, "SphericalLoxodromeUnitSpeed"]], {t, -10, 120}, PlotStyle -> Red, Axes -> None, BoxRatios -> {1, 1, 1}], meridians[\[Pi]/12]]$