Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Represent a spherical cap in 3D graphics
ResourceFunction["SphericalCap"][] represents a hemisphere. | |
ResourceFunction["SphericalCap"][p] represents a spherical cap with protrusion p. | |
ResourceFunction["SphericalCap"][p,prop] returns a given property prop. |
| "Surface" | BSplineSurface expression; default property |
| "Function" | explicit function corresponding to the BSplineSurface expression |
| "Formula" | explicit formula corresponding to the BSplineSurface expression |
| "ControlPoints" | control points of BSplineSurface expression |
| "Weights" | weights of BSplineSurface expression |
| "Properties" | list of all properties |
Show a hemisphere:
| In[1]:= |
| Out[1]= | 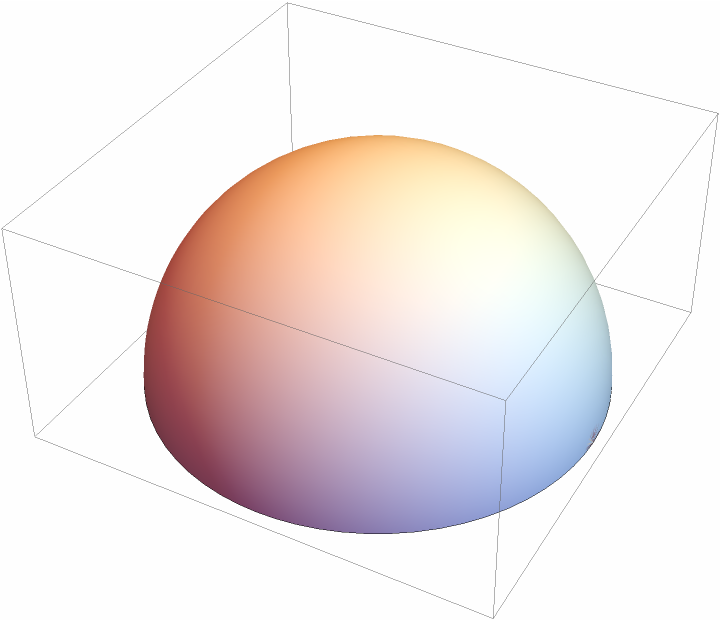 |
Show a spherical cap:
| In[2]:= |
| Out[2]= | 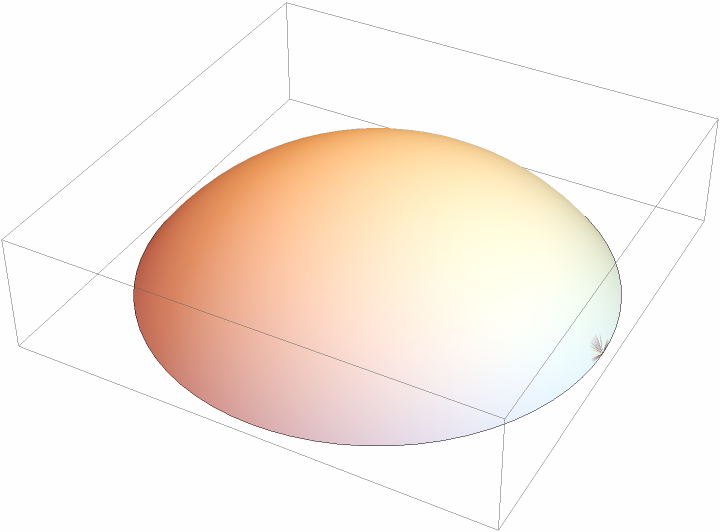 |
Apply styling:
| In[3]:= | ![Graphics3D[{Opacity[0.8], Orange, EdgeForm[{Purple, Dashed, Thickness[0.02]}], ResourceFunction["SphericalCap"][0.5]}]](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/03480de9e088b91d.png) |
| Out[3]= | 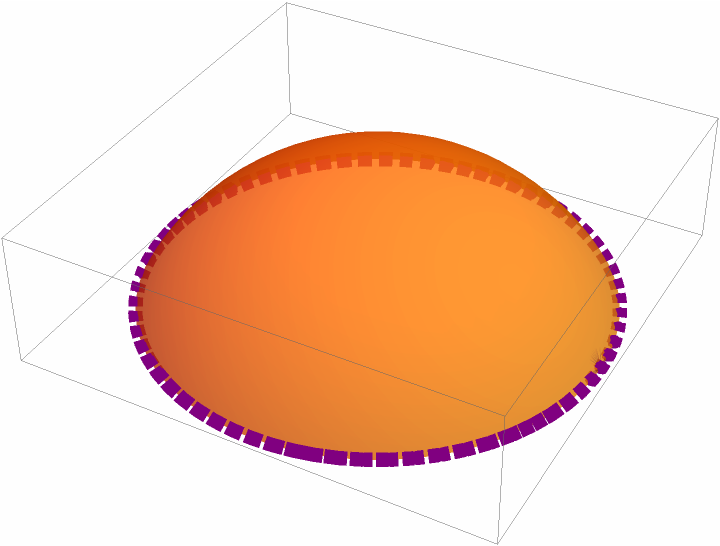 |
Spherical caps with different protrusion parameters:
| In[4]:= |
| Out[4]= |  |
As the parameter approaches -1, the cap approaches the unit sphere:
| In[5]:= |
| Out[5]= | 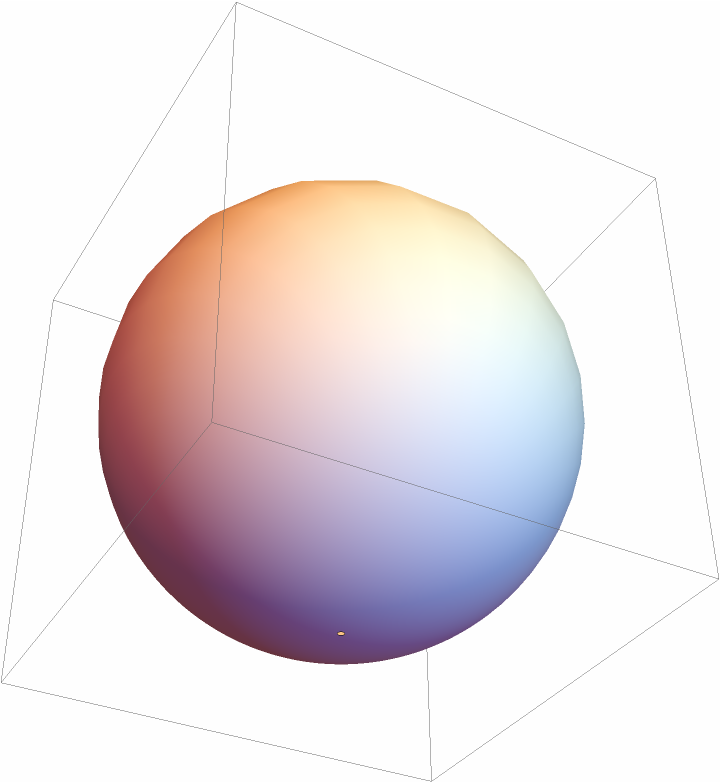 |
List all available properties:
| In[6]:= |
| Out[6]= |
By default, the "Surface" property is returned:
| In[7]:= | ![{
Graphics3D[ResourceFunction["SphericalCap"][]],
Graphics3D[ResourceFunction["SphericalCap"][0, "Surface"]]
}](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/5e6a3533591ebdb3.png) |
| Out[7]= | 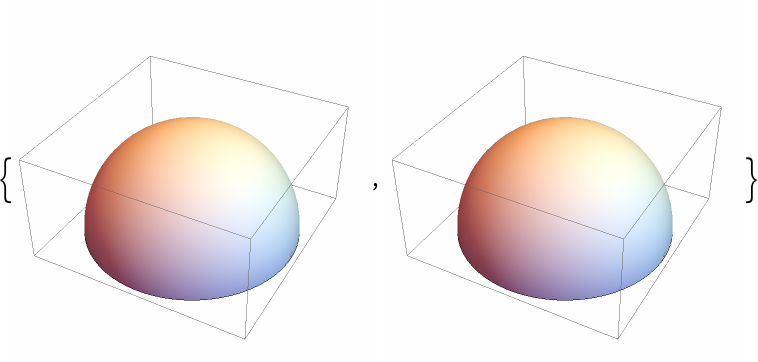 |
Retrieve the control points of the spline surface for a symbolic protrusion:
| In[8]:= |
| Out[8]= | 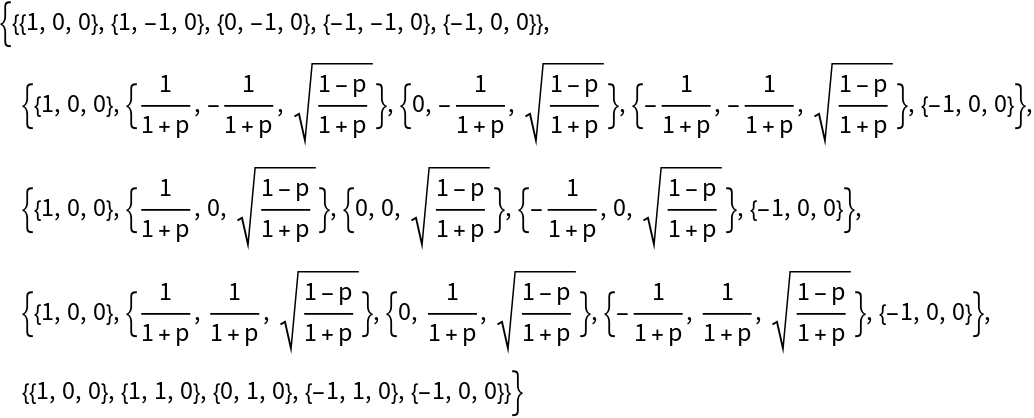 |
Retrieve the weights of the spline surface:
| In[9]:= |
| Out[9]= | 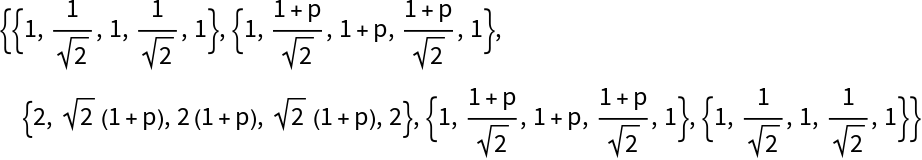 |
Get the function internally used by the spline surface:
| In[10]:= |
| Out[11]= | 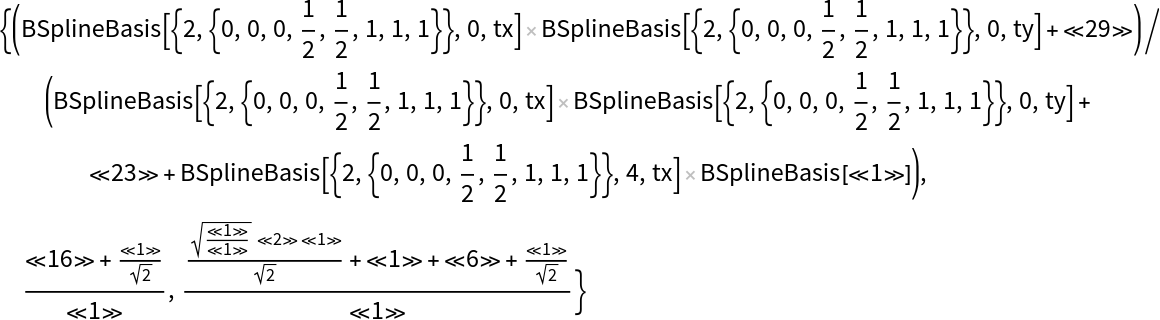 |
Plot the function for a specific protrusion parameter:
| In[12]:= |
| Out[12]= | 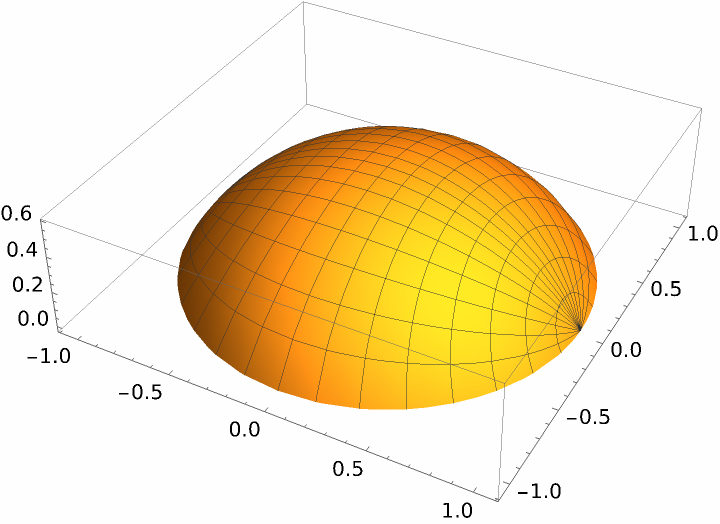 |
Consider only a part of the surface:
| In[13]:= | ![{txmin, txmax} = {0.1, 0.9};
{tymin, tymax} = {0.2, 0.3};
ParametricPlot3D[
ResourceFunction["SphericalCap"][0.5, "Function"][tx, ty], {tx, txmin, txmax}, {ty, tymin, tymax}, PlotRange -> 1, Mesh -> None]](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/1828da12a0a6e949.png) |
| Out[15]= | 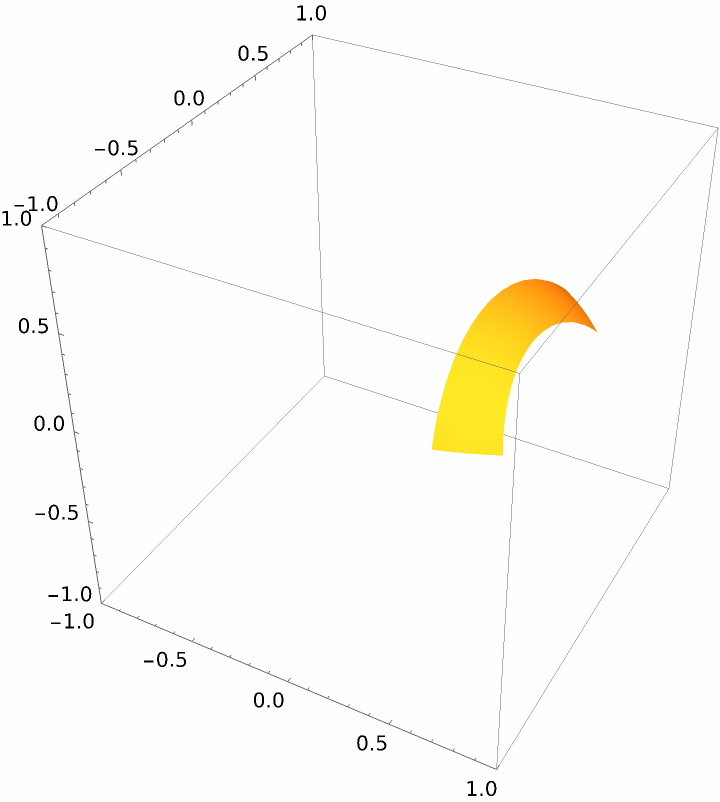 |
| In[16]:= | ![ParametricPlot3D[
ResourceFunction["SphericalCap"][0.5, "Function"][tx, ty], {tx, #1, #2}, {ty, #3, #4}, PlotRange -> 1, Mesh -> None] & @@@ {{0.5, 1, 0, 1}, {0, 1, 0.5, 1}, {0.2, 0.8, 0.2, 0.8}}](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/450a2a05cb661fe0.png) |
| Out[16]= |  |
Get the corresponding formula in formal variables x and y:
| In[17]:= |
| Out[18]= |  |
Create a bowl of water graphic:
| In[19]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/21a44d45-64ba-4cd4-bf94-53d76d0b7994"]](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/036563387cb4a89a.png) |
| Out[20]= |  |
Show a spherical lens:
| In[21]:= | ![lens = {Opacity[0.5], ResourceFunction["SphericalCap"][0.8], Rotate[ResourceFunction["SphericalCap"][0.8], \[Pi], {0, 1, 0}]};
Graphics3D[Rotate[lens, \[Pi]/2, {0, 1, 0}], Sequence[
ViewPoint -> {0.88, -2.98, 1.32}, Method -> {"SplinePoints" -> {40, 40}}, Boxed -> False]]](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/244fd67557fabb4b.png) |
| Out[22]= | 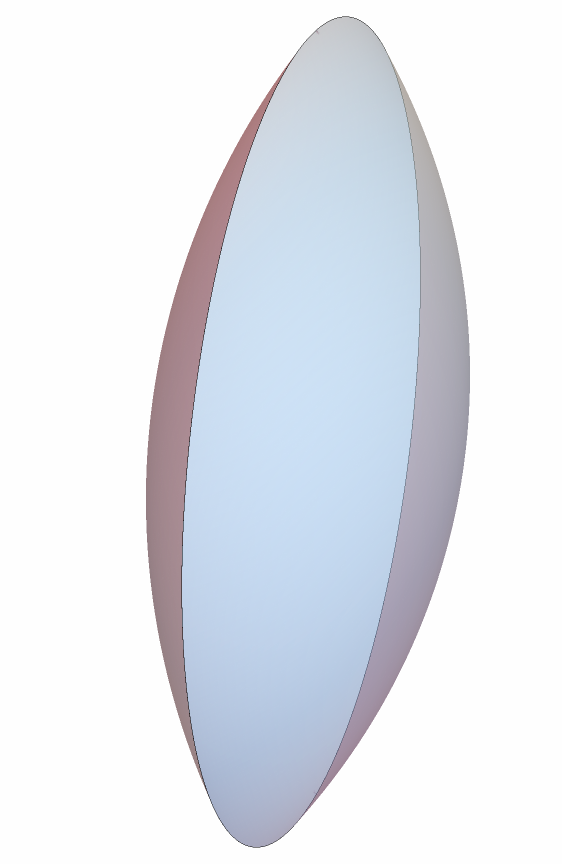 |
Obtain a spherical cap using Ball and ClipPlanes:
| In[23]:= | ![Manipulate[
Graphics3D[{Opacity[0.5], Style[Scale[Ball[{0, 0, -p}], If[scale, 1, 1/Sqrt[1 - p^2]], {0, 0, 0}], ClipPlanes -> InfinitePlane[{0, 0, 0}, {{1, 0, 0}, {0, 1, 0}}]]}, PlotRange -> 2], {{p, 0}, -1, 1}, {{scale, False}, {True, False}}]](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/3fbf6816fd6fdb7b.png) |
| Out[23]= | 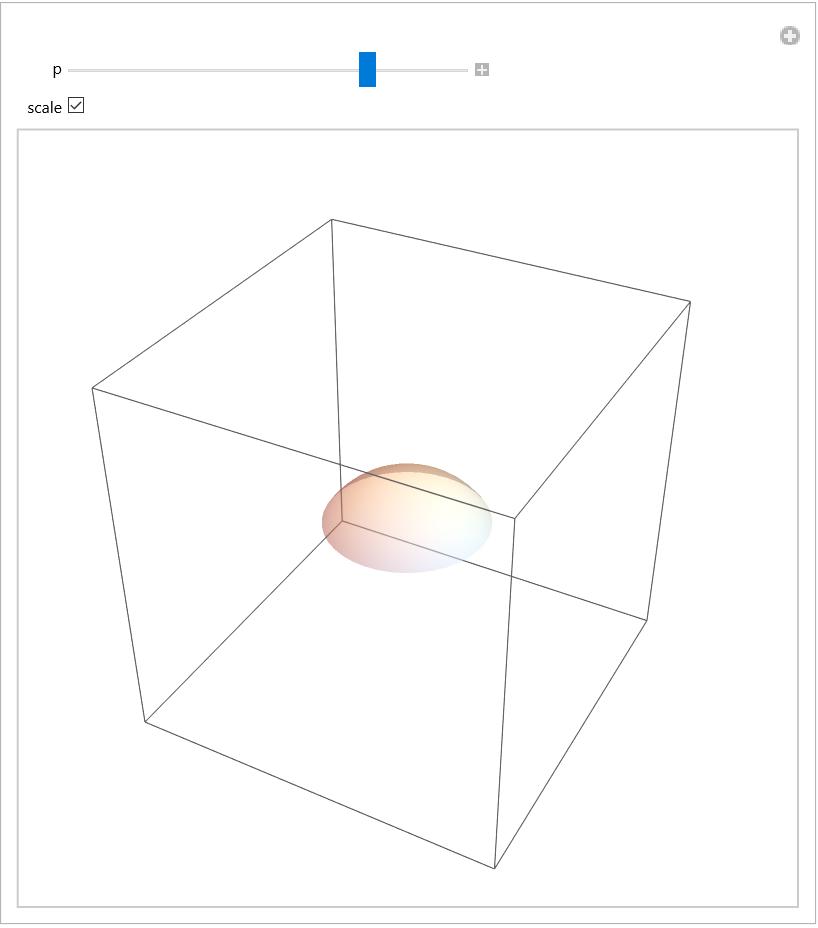 |
Obtain a spherical cap using SphericalPlot3D:
| In[24]:= | ![Manipulate[
limang = ArcCos[p];
cap = SphericalPlot3D[
1, {\[Theta], -limang, limang}, {\[Phi], -\[Pi]/2, \[Pi]/2}];
cap = First@Cases[cap, _GraphicsComplex, Infinity, 1];
Graphics3D[
Scale[Translate[cap, {0, 0, -p}], If[scale, 1, 1/Sqrt[1 - p^2]], {0, 0, 0}], Axes -> True]
, {{p, 0}, -1 + 0.01, 1 - 0.01}, {{scale, False}, {True, False}}]](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/5664c6f0900874bb.png) |
| Out[24]= | 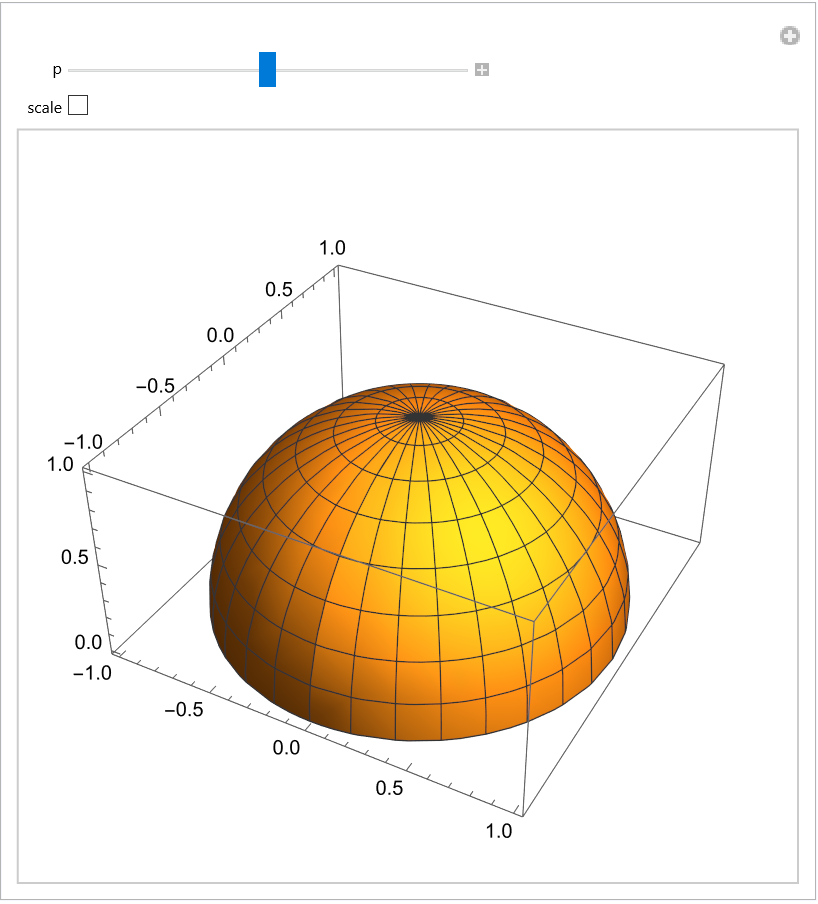 |
Represent a flat 3D disk:
| In[25]:= |
| Out[25]= | 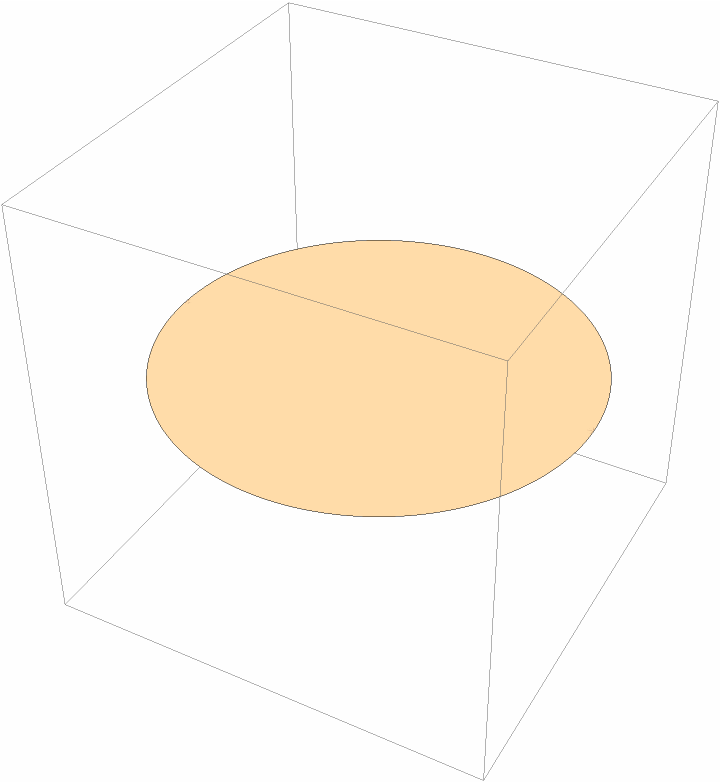 |
Compare with the resource function Disk3D:
| In[26]:= |
| Out[26]= | 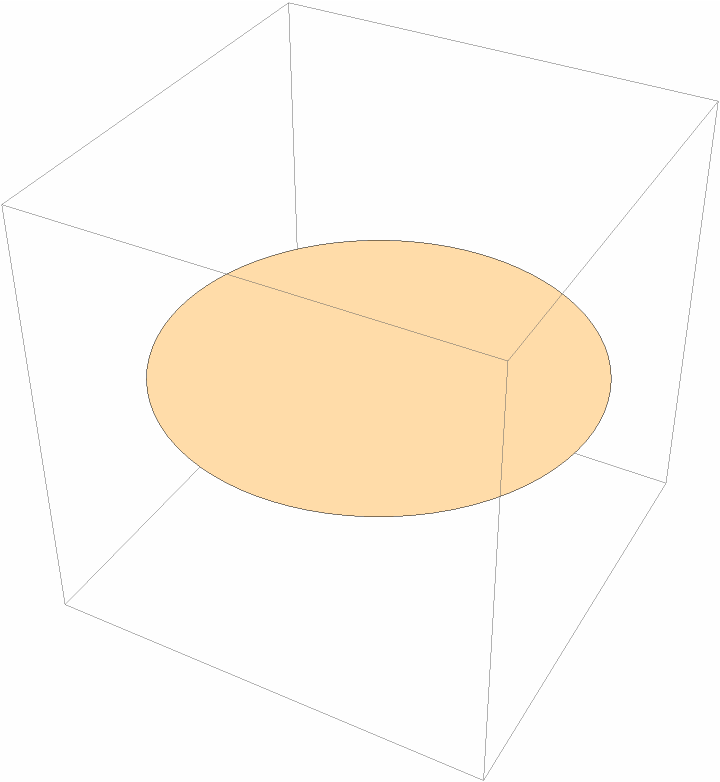 |
Despite the stark similarity, the underlying spline surfaces differ substantially:
| In[27]:= |
| Out[27]= | 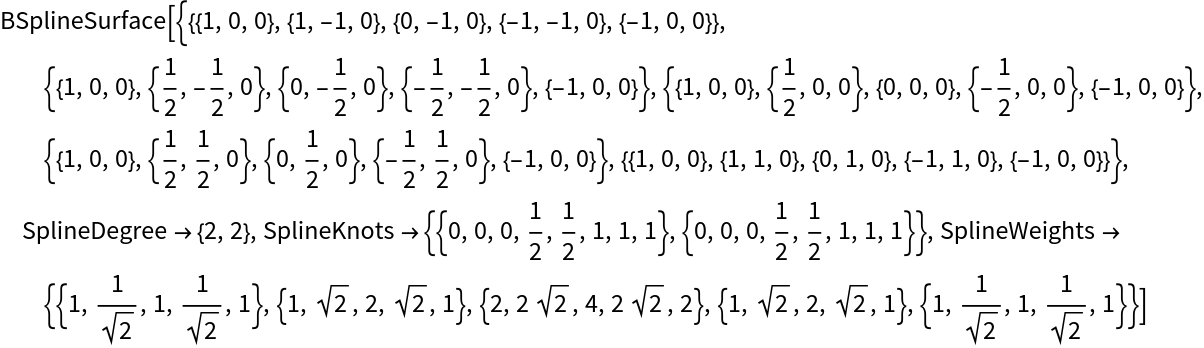 |
| In[28]:= |
| Out[28]= | 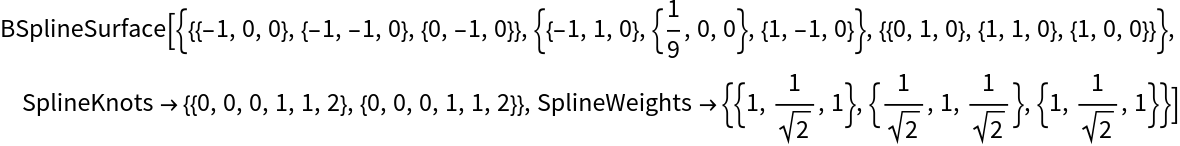 |
Move, scale, and rotate the cap:
| In[29]:= | ![cap = ResourceFunction["SphericalCap"][0.8];
{
Graphics3D[Translate[cap, {1, 0, 1.2}], Axes -> True, PlotRange -> 2],
Graphics3D[Scale[cap, 2], Axes -> True, PlotRange -> 2],
Graphics3D[Rotate[cap, \[Pi]/2, {0, 1, 0}], Axes -> True, PlotRange -> 2]
}](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/6be0cef4ea24560b.png) |
| Out[30]= | 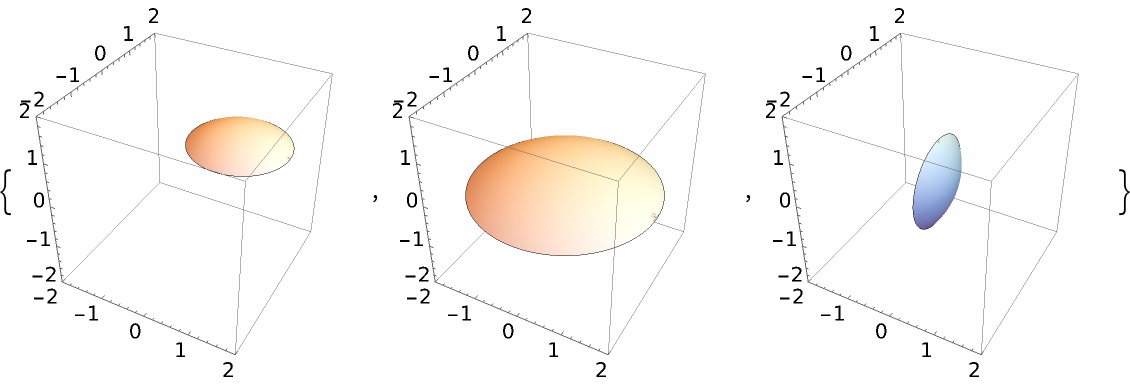 |
A spherical cap returned by SphericalCap satisfies the equation for a shifted (unit) sphere:
| In[31]:= | ![cap = ResourceFunction["SphericalCap"][p, "Formula", False];
{x, y, z} = PiecewiseExpand[cap, 0 <= \[FormalX] < 1/2 && 0 <= \[FormalY] < 1/2] // Quiet;
sphereEq = x^2 + y^2 + (z + p /Sqrt[1 - p^2])^2 == 1/(1 - p^2);
Simplify[sphereEq, {-1 < p < 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/4ad3db02ec7b4bc6.png) |
| Out[34]= |
Artefacts occur at poles:
| In[35]:= |
| Out[35]= | 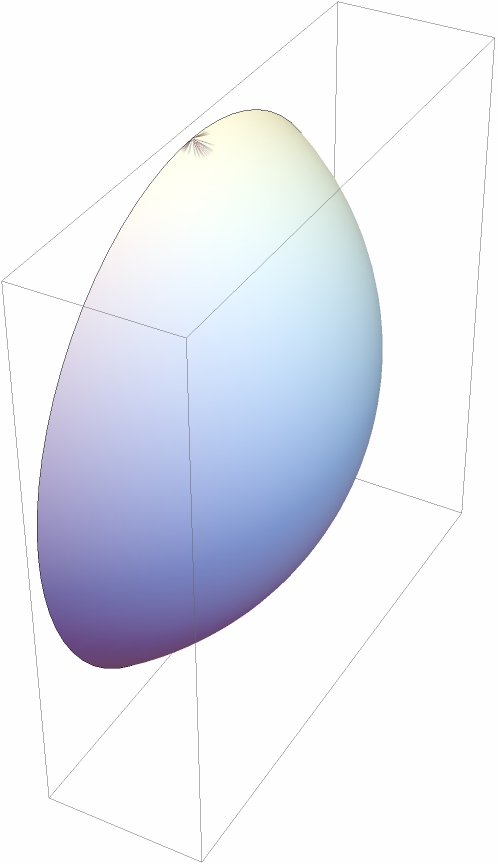 |
Increase the rendering parameter for spline surfaces to mitigate the artefacts:
| In[36]:= |
| Out[36]= | 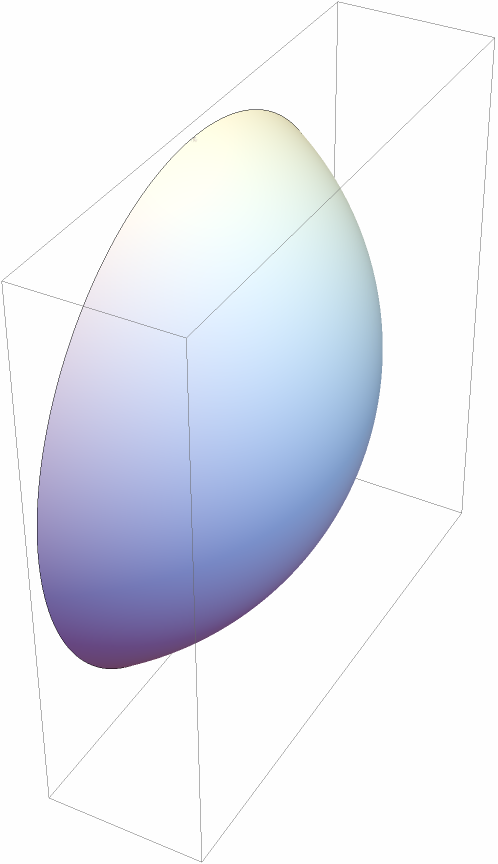 |
The protrusion parameter cannot be set exactly to -1:
| In[37]:= |
| Out[37]= |  |
For such a case, use Ball instead:
| In[38]:= | ![{
Graphics3D[ResourceFunction["SphericalCap"][-0.99], ViewPoint -> {-1.3`, -2.4`, 2.`}, Method -> {"SplinePoints" -> {30, 30}}],
Graphics3D[Ball[], ViewPoint -> {-1.3`, -2.4`, 2.`}]
}](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/5fd9b1ef80fd29ef.png) |
| Out[38]= | 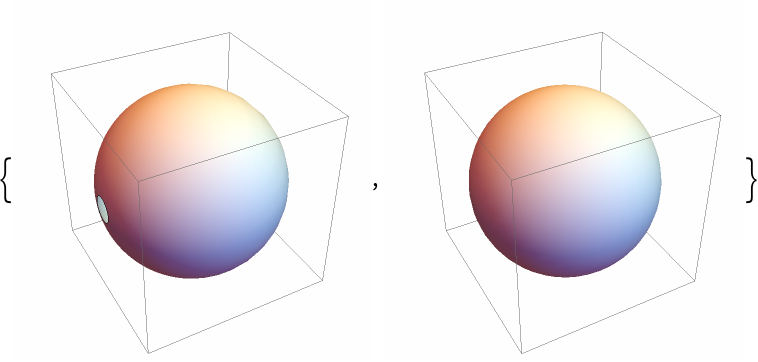 |
Bubbles made by a bubble wand:
| In[39]:= | ![wand = {Gray, Torus[{0, 0, 0}, {0.8, 1.1}], Cylinder[{{0.9, 0, 0}, {5, 0, 0}}, 0.1]};
bubbles = {Opacity[0.5], ResourceFunction["SphericalCap"][0], Ball[Table[{RandomReal[], RandomReal[], 1 + i}, {i, 5}], RandomReal[{0, 1}, 5]]};
Graphics3D[Rotate[{wand, bubbles}, \[Pi]/2, {0, 1, 0}], ViewPoint -> {-1.3, -2.4, 2.}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/2504dd5b4b4d9139.png) |
| Out[40]= | 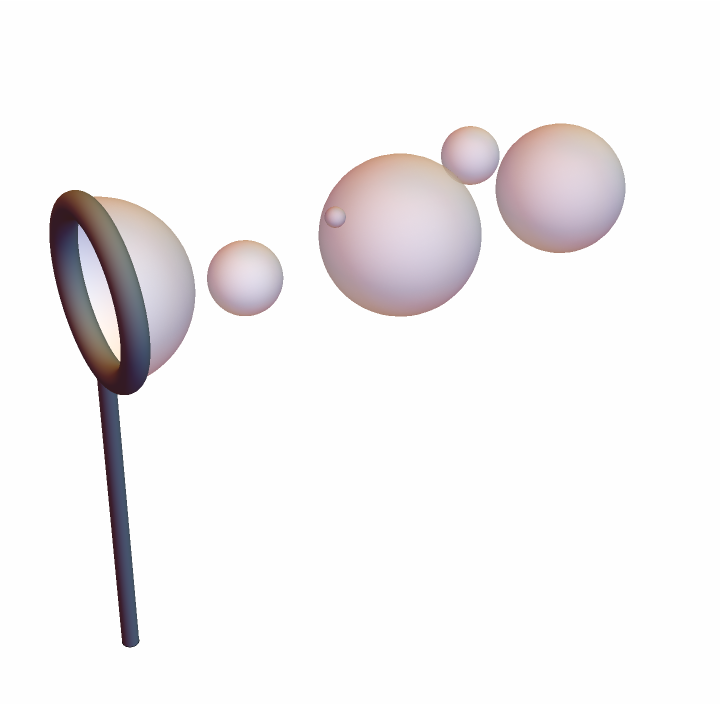 |
Visualize the control points:
| In[41]:= | ![cols = {Yellow, Red, Green, Blue, Black};
Manipulate[
arrx = ResourceFunction["SphericalCap"][p, "ControlPoints"];
Graphics3D[{PointSize[0.02], Table[{cols[[idx]], Line[arrx[[idx]]], Point[arrx[[idx]]]}, {idx, Range[5]}], Opacity[0.5, Gray], ResourceFunction["SphericalCap"][p]}, PlotRange -> {3 {-1, 1}, 3 {-1, 1}, {0, 4}}, Axes -> True], {{p, 0}, -1 + 0.01, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/233120b63eee320c.png) |
| Out[42]= | 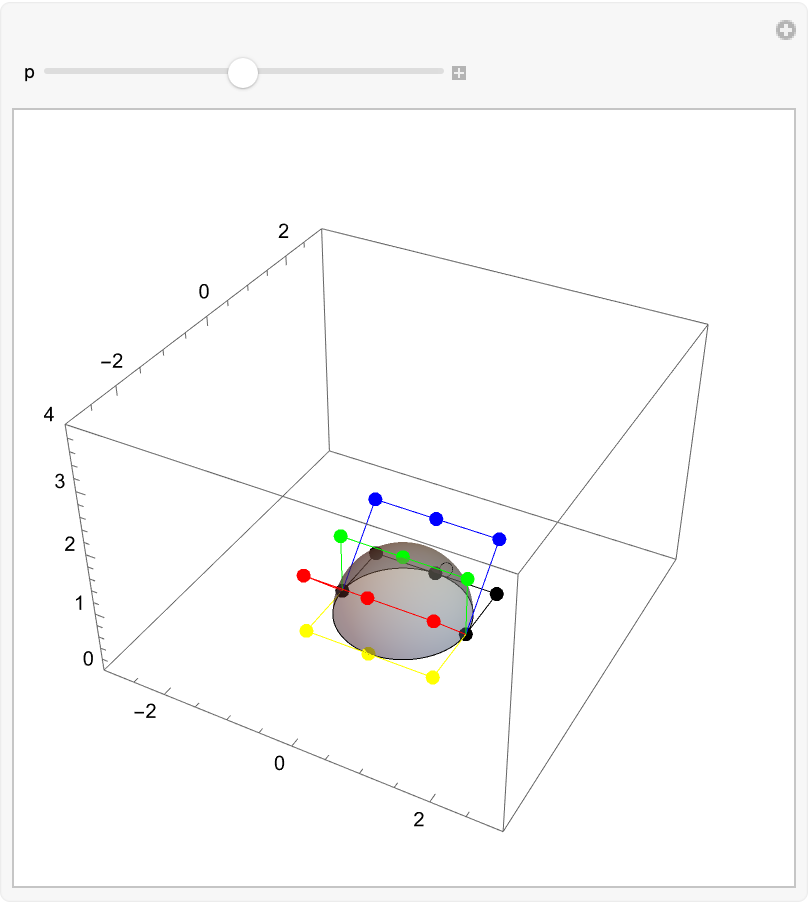 |
Visualize the weights:
| In[43]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/25c302d7-684d-44c5-9c39-6a871981cd10"]](https://www.wolframcloud.com/obj/resourcesystem/images/630/63054714-f488-410b-8633-1640cf23e5a2/3d3b7f02f39349b4.png) |
| Out[44]= | 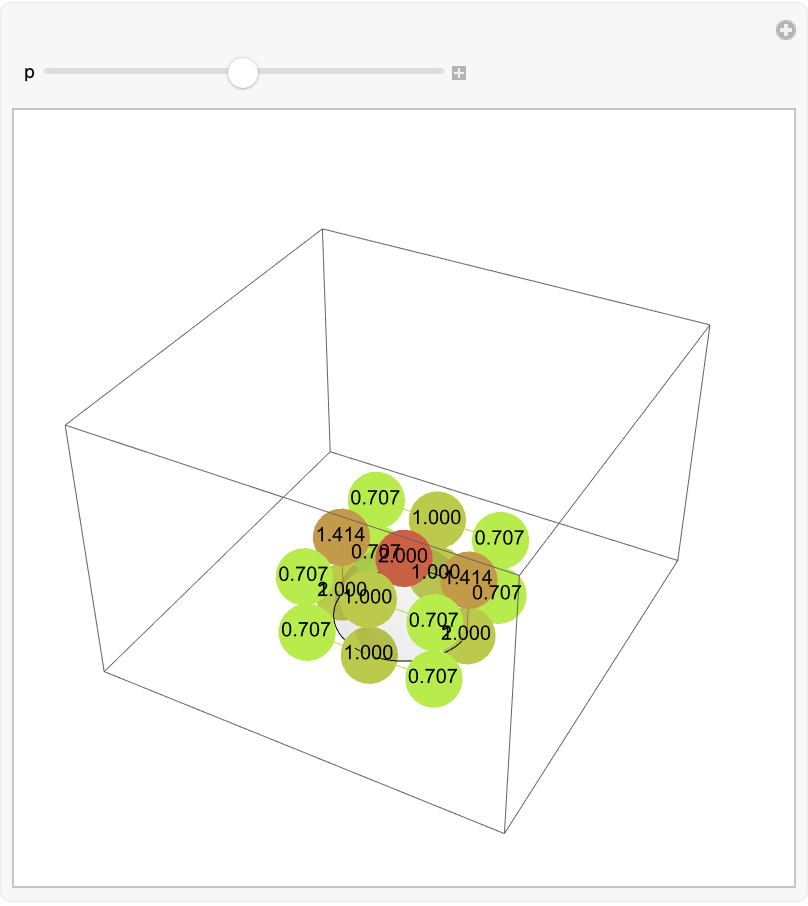 |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License