Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SphericAnamorphosisMap

Source Notebook

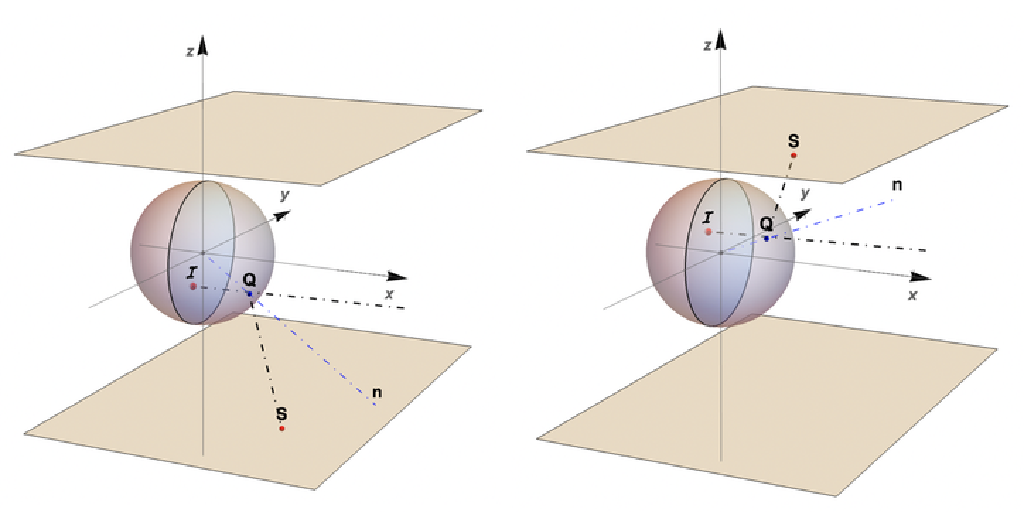
Convert a point reflected in a spherical mirror to its spherical anamorphosis map in a plane parallel to the xy-plane

Contributed by: Erik Mahieu

ResourceFunction["SphericAnamorphosisMap"][{yi,zi},h]

converts the point {0,yi,zi} inside a spherical mirror to its spherical anamorphosis map.

Details and Options

The anamorphosis map (the point S) is in the plane z=h if zi>0 or z=-h if zi<0. The value of h must be a positive real number. The sign of h is taken to be the sign of zi.
The function converts points I in the yz-plane into anamorphic points S in the (z=h)-plane. The point I is the reflection of S. The spherical mirror has a radius of 1.
As a result of the symmetry of the sphere related to the three coordinate axes, only the distance of the viewpoint from the center of the mirror is relevant.
As the radius of the mirror is small compared to the viewpoint distance, the latter is taken to be at x=Infinity.
The range of the function is Disk[ ] in the yz-plane.
The default anamorphosis plane is z=±1.

Examples

Basic Examples (2) 

Get the anamorphic map in the plane z=2 of a point {-.15,.1} reflected in a spherical mirror:

In[1]:=
ResourceFunction["SphericAnamorphosisMap"][{-.15, .1}, 1]
Out[1]=

Get the anamorphic map in the plane z=-2 of a point reflected in a spherical mirror as {-.15,-.1} in the yz-plane:

In[2]:=
ResourceFunction["SphericAnamorphosisMap"][{-.15, -.1}, 2]
Out[2]=

Scope (2) 

Points can be combined to form simple designs such as arrows:

In[3]:=
arrowFloor = {{0, 0.575`, -0.625`}, {0, 0.575`, -0.375`}, {0, -0.175`, -0.375`}, {0, -0.175`, -0.28125`}, {0, -0.6125`, -0.5`}, {0, -0.175`, -0.71875`}, {0, -0.175`, -0.625`}, {0, 0.575`, -0.625`}, {0, 0.575`, -0.625`}};
In[4]:=
arrowCeiling = -arrowFloor;
In[5]:=
anaArrows = Map[ResourceFunction["SphericAnamorphosisMap"][Rest@#, 2] &, {arrowFloor, arrowCeiling}, {2}];

This 3D plot shows two arrows reflected in a spherical mirror and their anamorphic maps in the planes z=±2:

In[6]:=
Graphics3D[{Thick, MapThread[{#1, Line@#2} &, {{Red, Blue}, {{arrowFloor, anaArrows[[1]]}, {arrowCeiling, anaArrows[[2]]}}}], Opacity[.35], Sphere[]}]
Out[6]=

Applications (2) 

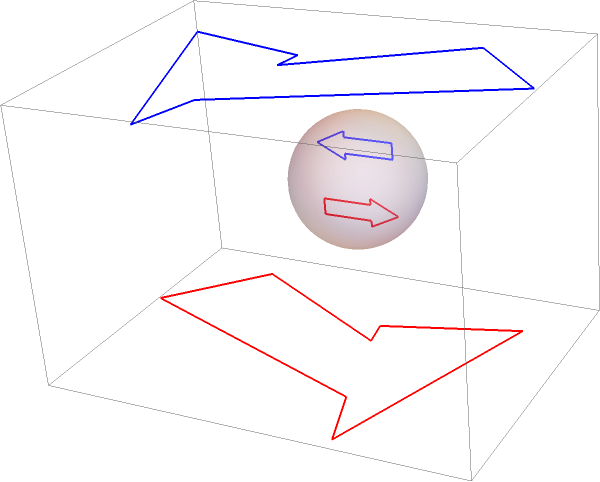A classical example is a deformed anamorphic text message that can be reflected undeformed in a spherical mirror.

Convert a text into a set of point coordinates:

In[7]:=
math = (First[ First[ImportString[ ExportString[ Style["\[Star]\[HeartSuit] I Love You \[HeartSuit]\[Star]", FontFamily -> "Times", FontSize -> 72], "PDF"], {"PDF", "Pages"}, "TextMode" -> "Outlines"]]] /. FilledCurve :> JoinedCurve /. {x_?NumericQ, y_?NumericQ} :> {x, y}*.0047 /. {x_?NumericQ, y_?NumericQ} :> {x - .9, y - .40})[[-1, 1, All, -1]];

After conversion of the point coordinates to their anamorphic map:

In[8]:=
anamath = ParallelMap[Most[ResourceFunction["SphericAnamorphosisMap"][#1]] &, math, {3}]; Graphics[{{DotDashed, Circle[]}, {AbsoluteThickness[3], Map[Line[#1] &, anamath, {2}]}}]
Out[9]=

Possible Issues (2) 

The sign of zi determines the sign of h or the location of the anamorphosis plane z=h:

In[10]:=
ResourceFunction["SphericAnamorphosisMap"][{0.25, #}, 2] & /@ {-.1, .1} // Column
Out[10]=

Points with z-coordinates close to the equator z=0 have their anamorphosis map approaching infinity and should be avoided:

In[11]:=
ResourceFunction["SphericAnamorphosisMap"][{0.25, .01}, 2]
Out[11]=

Publisher

Erik Mahieu

Version History

  • 1.0.0 – 21 December 2020

Related Resources

License Information