Function Repository Resource:

SphereFit

Source Notebook

Find the best-fit sphere for a set of points

Contributed by: Sander Huisman

ResourceFunction["SphereFit"][pts]

returns the best-fit Sphere for the points pts.

ResourceFunction["SphereFit"][w→pts]

returns the best-fit Sphere using the weights w.

ResourceFunction["SphereFit"][pts,"Association"]

returns an Association with the center, radius, Sphere, and a pure function defining the sphere.

Details

SphereFit returns a Sphere object or an Association.

For 5 or more points pts, ResourceFunction["SphereFit"] returns the Sphere centered at {x,y,z} with radius r that minimizes

If there are weights w_i it minimizes

For 1 point, a Sphere at that point with a radius of 0 is returned.

For 2 points, a Sphere centered at the midpoint with a radius equal to half the distance between the points is returned.

For 3 points that are not collinear, a Sphere with a great circle equal to the circumcircle is returned.

For 4 or more points that are not coplanar, a Sphere is fitted.

Examples

Basic Examples (2)

Find the best-fit Sphere for the given points:

In[1]:=

Out[2]=

See the result along with the points:

In[3]:=

Out[5]=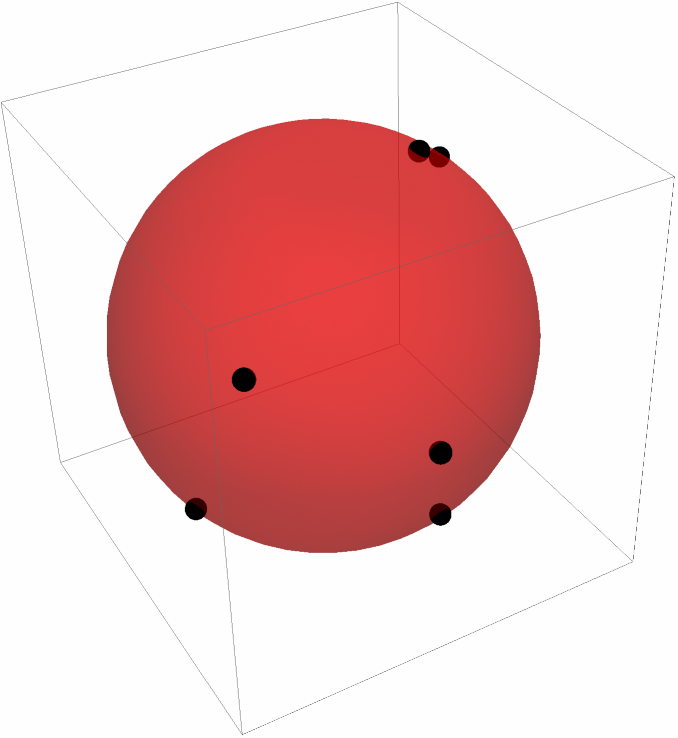

Fit a sphere through a noisy 1000 points:

In[6]:=

pts = Normalize /@ RandomVariate[NormalDistribution[], {1000, 3}];
pts *= RandomVariate[NormalDistribution[5, 0.25], Length[pts]];
pts += Threaded[{100, 200, 300}];
Graphics3D[{Black, Sphere[pts, 0.1], Red, Opacity[0.5], ResourceFunction["SphereFit"][pts]}]

Out[9]=

Scope (2)

Get all the properties:

In[10]:=

Out[11]=

Use the "Function" to create a definition of the sphere:

In[12]:=

Out[12]=

Specify weights for outliers:

In[13]:=

pts = {{-1, -1, -1}, {-1, -1, 1}, {-1, 1, -1}, {-1, 1, 1}, {1, -1, -1}, {1, -1, 1}, {1, 1, -1}, {1, 1, 3}};
weights = {1, 1, 1, 1, 1, 1, 1, 0.1};
Graphics3D[{Black, Sphere[pts, 0.2], Red, Opacity[0.5], ResourceFunction["SphereFit"][weights -> pts]}]

Out[15]=

Properties and Relations (3)

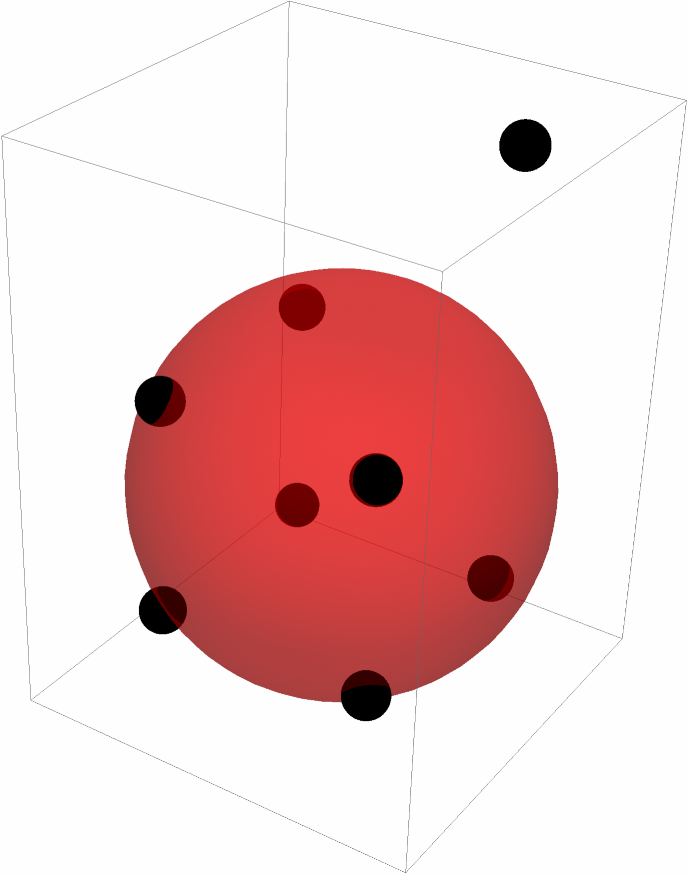For two points, the fit goes through both:

In[16]:=

Out[17]=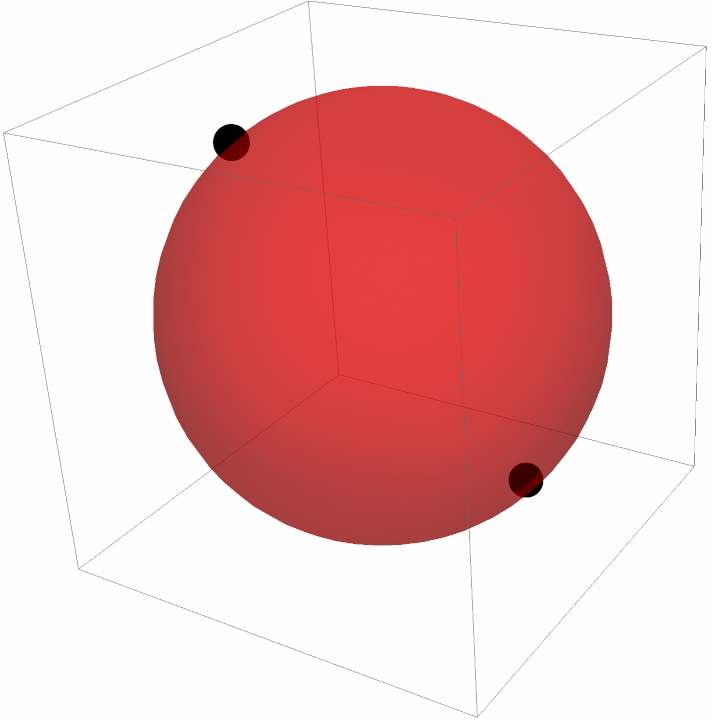

For three points, the fit goes through all the points:

In[18]:=

Out[19]=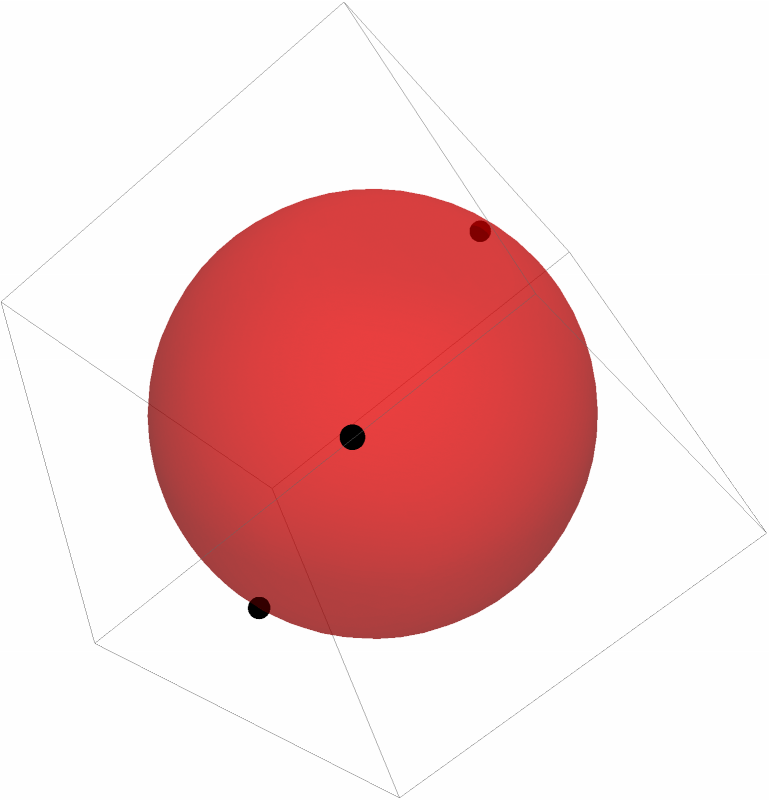

For four points, the fit goes through all the points:

In[20]:=

Out[21]=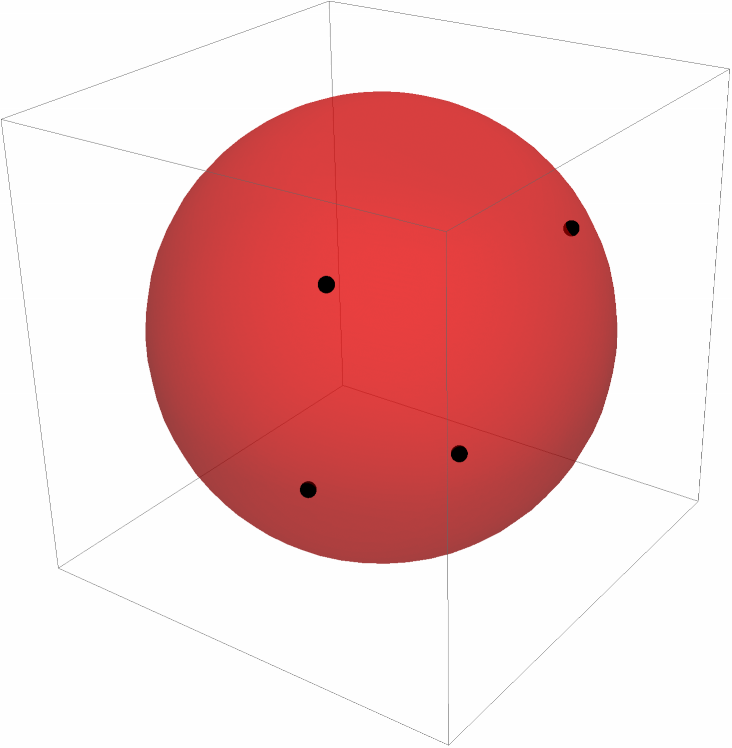

If the points fall on a sphere and cover more than a hemisphere, BoundingRegion can give similar results:

In[22]:=

pts = Normalize /@ RandomVariate[NormalDistribution[], {1000, 3}];
pts += Threaded[{100, 200, 300}];
{ResourceFunction["SphereFit"][pts], BoundingRegion[pts, "MinBall"]}

Out[24]=

Possible Issues (2)

When 3 points are given and they are collinear, a Failure object is returned:

In[25]:=

Out[25]=

When 4 or more points are given and they are coplanar, a Failure object is returned:

In[26]:=

SeedRandom[1234];
pts = Table[{0, -1, 3} + t {2, 3, 4}, {t, RandomVariate[NormalDistribution[], 5]}];
ResourceFunction["SphereFit"][pts]

Out[27]=

Neat Examples (1)

Fit points that only lay on one-eighth of a sphere:

In[28]:=

$pts = Normalize /@ RandomVariate[NormalDistribution[], {10000, 3}]; pts //= Select[#[[1]] > 0 \[And] #[[2]] > 0 \[And] #[[3]] > 0 &]; pts *= RandomVariate[NormalDistribution[1, 0.05], Length[pts]]; pts += Threaded[{100, 200, 300}]; Graphics3D[{pts // Point, Opacity[0.5], Red, ResourceFunction["SphereFit"][pts]}]$