Basic Examples (4) 

Depict a Mystic tile and a Spectre tile:

In[1]:=

Out[1]=

Generate a tiling made of Mystic and Spectre tiles:

In[2]:=

Out[2]=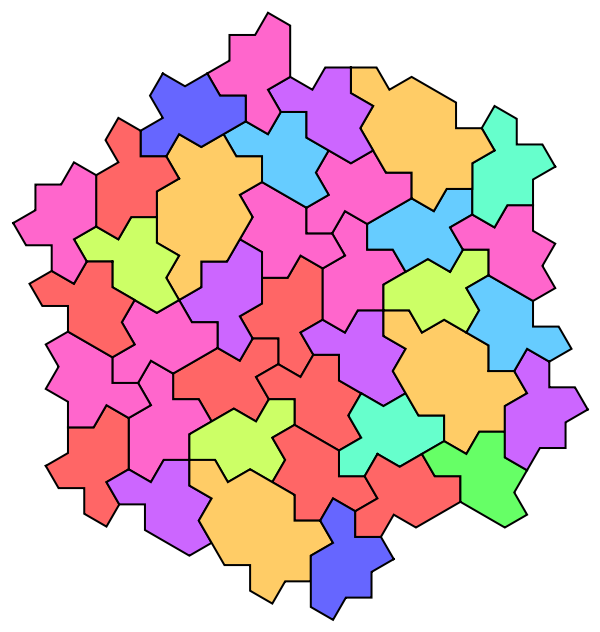

Plot the tilings of combinatorial hexagons, the Spectre tiles and supertiles:

In[3]:=

Out[3]=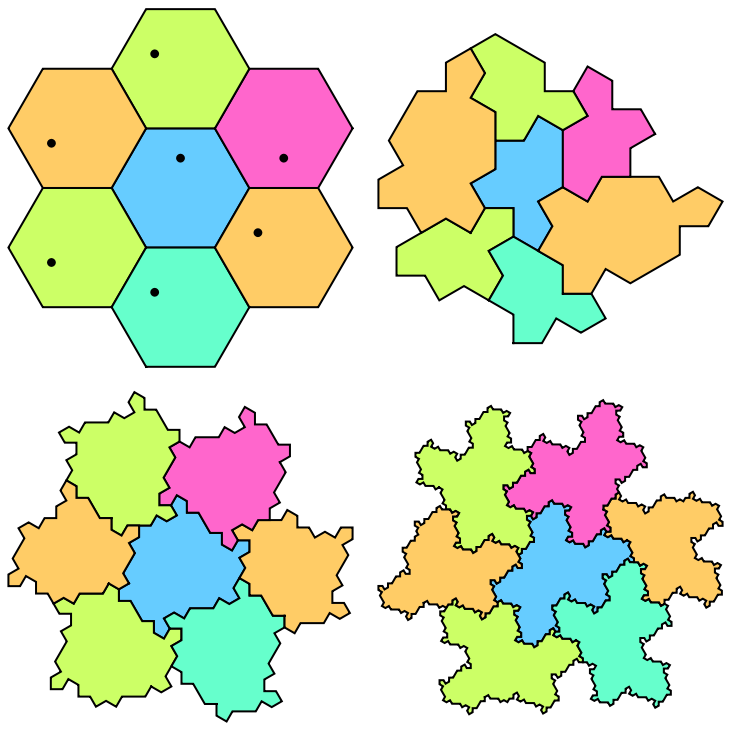

Make a curved spectre tiling:

In[4]:=

Out[4]=

Scope (3) 

There are 9 different initial conditions, corresponding to 9 kinds of hexagons:

In[5]:=

Out[5]=

Curve the spectre tiles and supertiles:

In[6]:=

Out[6]=

Any higher-level supertiles are available:

In[7]:=

Out[7]=

Options (8) 

Count (2) 

Use "Count" to give more possible tilings:

In[8]:=

Out[8]=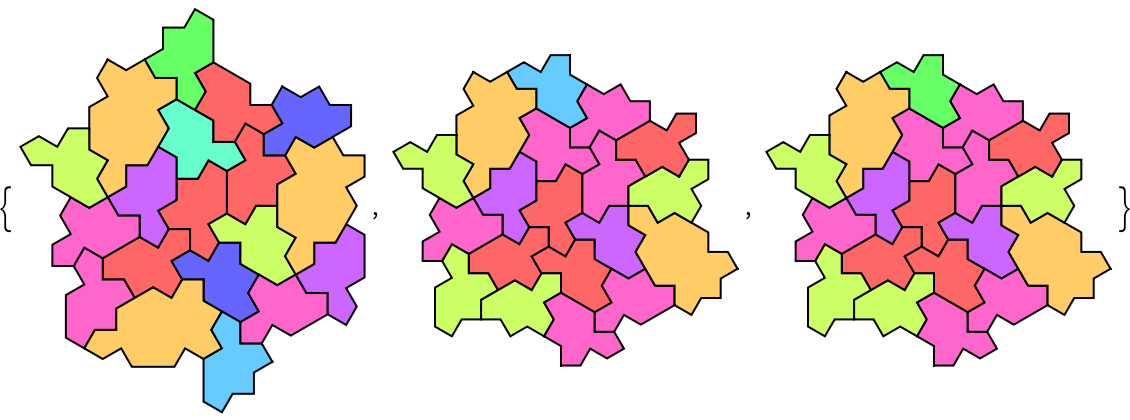

Generate all valid one layer surroundings:

In[9]:=

Out[9]=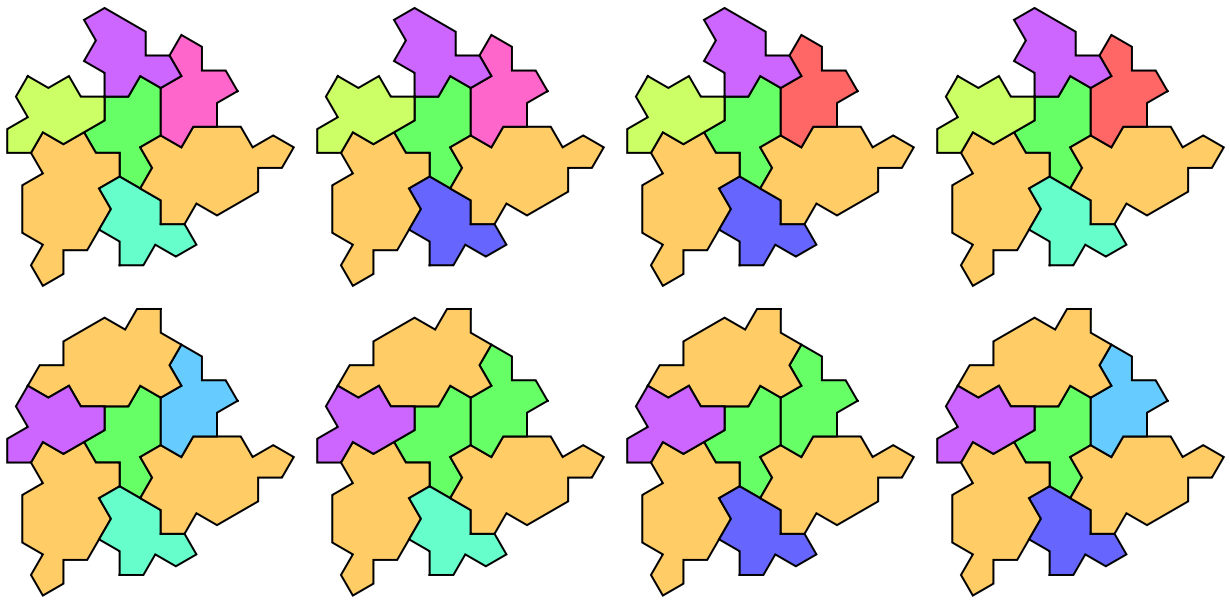

Colors (3) 

Color the tiling using GrayLevel:

In[10]:=

Out[10]=

Add blue EdgeForm in a tiling:

In[11]:=

Out[11]=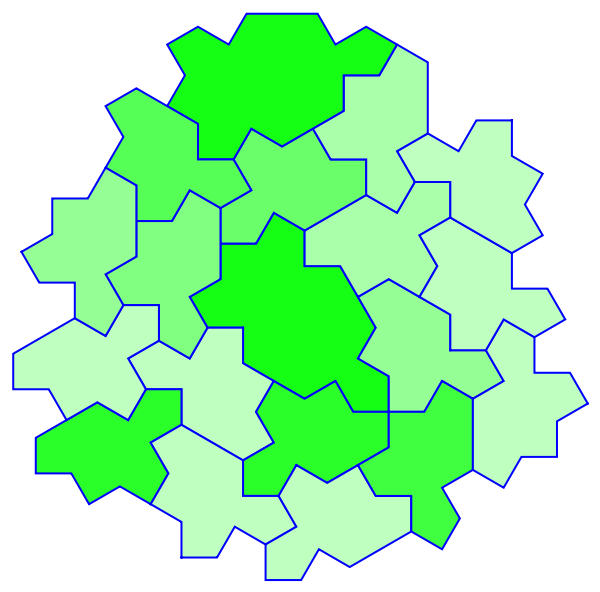

The same style can be set by ColorFunction:

In[12]:=

Out[12]=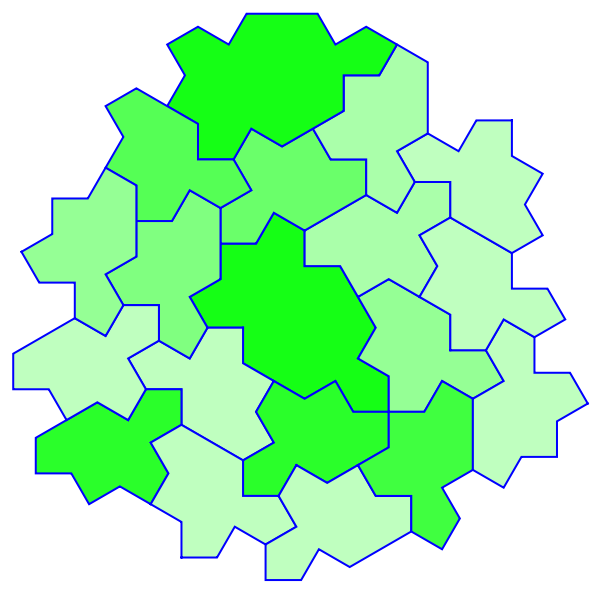

EdgeShapeFunction (2) 

Set EdgeShapeFunction to be Automatic to plot curved tilings:

In[13]:=

Out[13]=

Plot the curved Spectre tiling with different edges function:

In[14]:=

Out[14]=

InterpolationPoints (1) 

The function uses interpolation to make curved boundary. Interpolation options can be set manually:

In[15]:=

Out[15]=

Properties and Relations (1) 

It is faster to use a list of types than to map over a list:

In[16]:=

Out[16]=

In[17]:=

Out[17]=

They give exactly the same result, even if the option "Count" is not 1.

In[18]:=

Out[18]=

Possible Issues (2) 

EdgeShapeFunction doesn’t work on hexagons:

In[19]:=

Out[19]=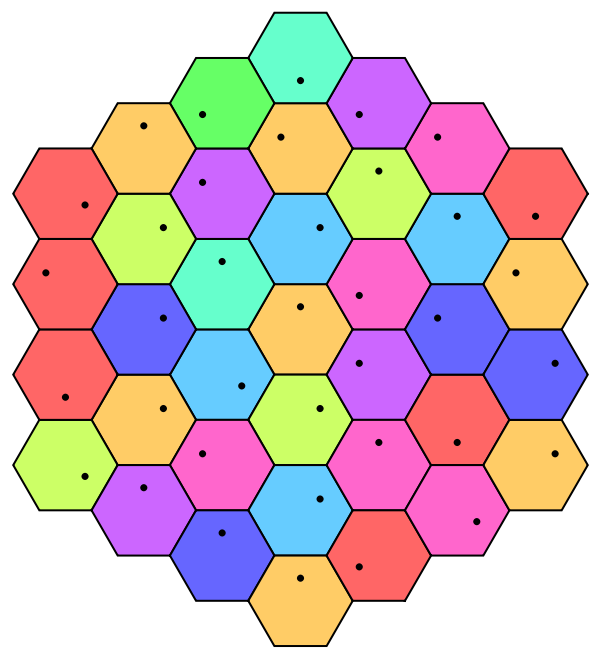

The EdgeShapeFunction should be continuous from 0 to 1, and equal to zero at both 0 and 1. Otherwise, the shape would collapse. Also, if the value of the function increase to a large value, it may cause self-intersection:

In[20]:=

Out[20]=

Neat Examples (1) 

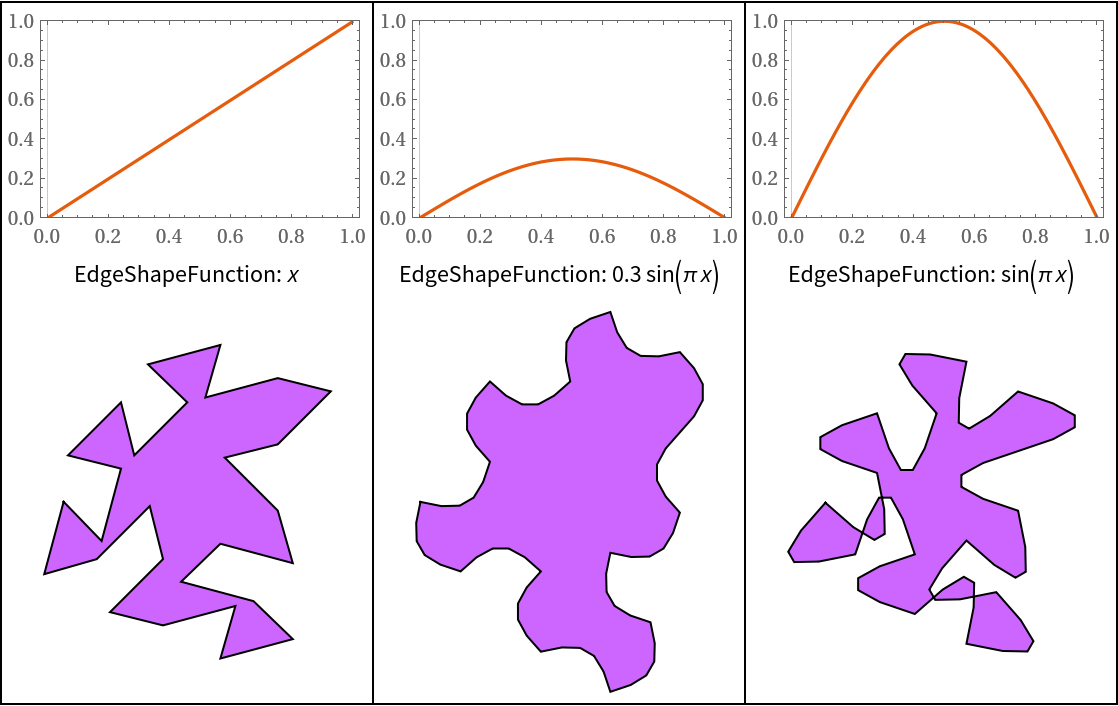Plot a large patch of spectre tiling, coloring Mystic purple and one of its neighboring tiles green:

In[21]:=

Out[21]=