Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Count the number of labeled spanning trees in a graph
ResourceFunction["SpanningTreeCount"][g] gives the number of labeled spanning trees of the graph g. |
Find the number of spanning trees of a graph:
| In[1]:= |
| Out[1]= | 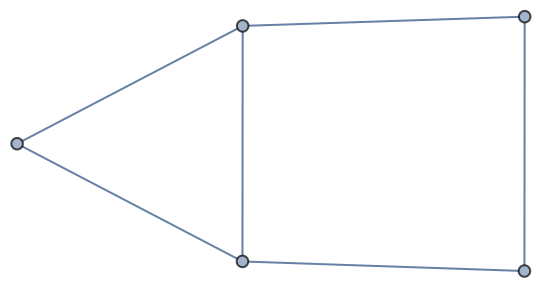 |
| In[2]:= |
| Out[2]= |
A tree contains exactly one spanning tree:
| In[3]:= |
| Out[3]= | 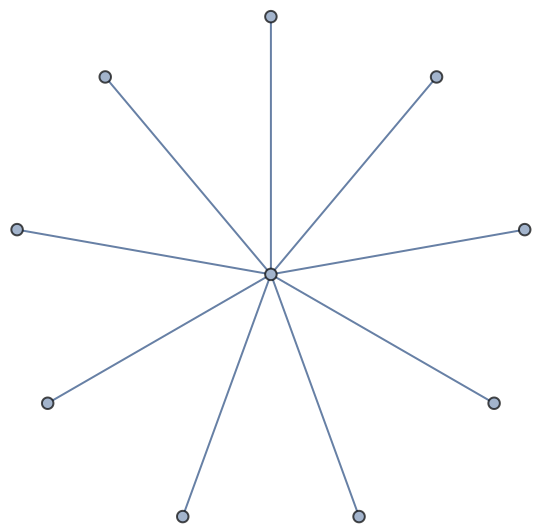 |
| In[4]:= |
| Out[4]= |
A cycle on n vertices contains exactly n spanning trees, since deleting any edge creates a tree:
| In[5]:= |
| Out[5]= | 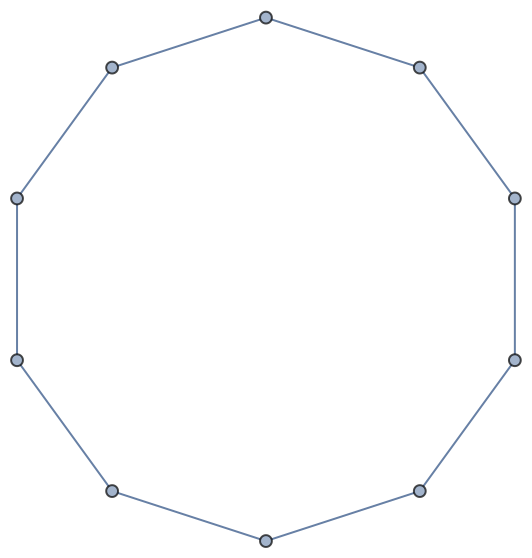 |
| In[6]:= |
| Out[6]= |
The number of spanning trees of a complete graph is nn-2, as was proved by Cayley:
| In[7]:= |
| Out[7]= | 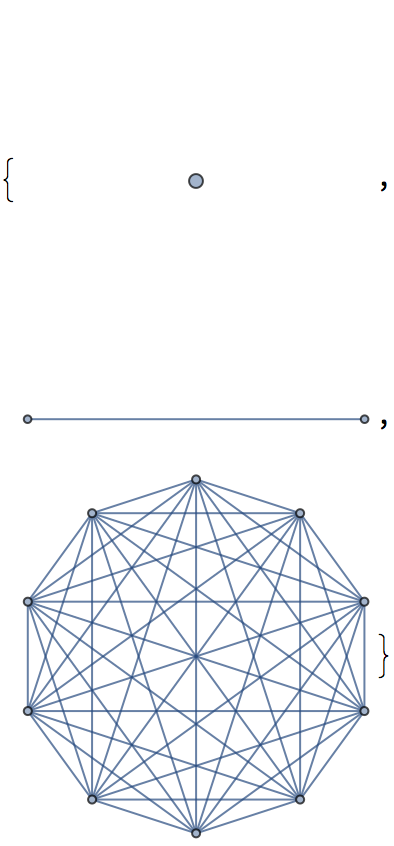 |
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
GraphData[name,"SpanningTreeCount"] gives the number of spanning trees for a named graph:
| In[10]:= |
| Out[10]= | 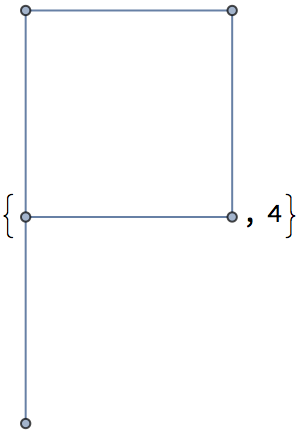 |
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= | 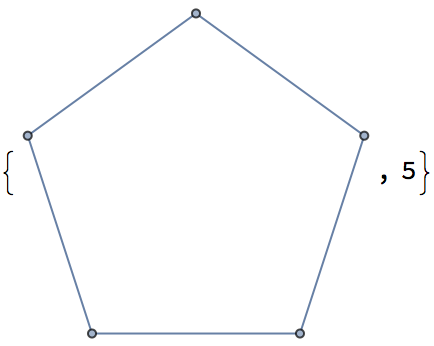 |
| In[13]:= |
| Out[13]= |
This work is licensed under a Creative Commons Attribution 4.0 International License