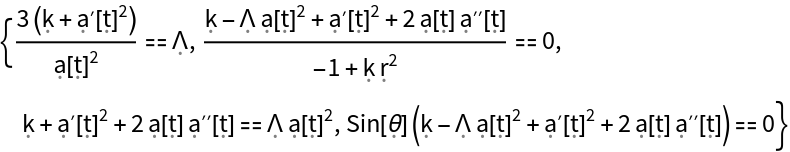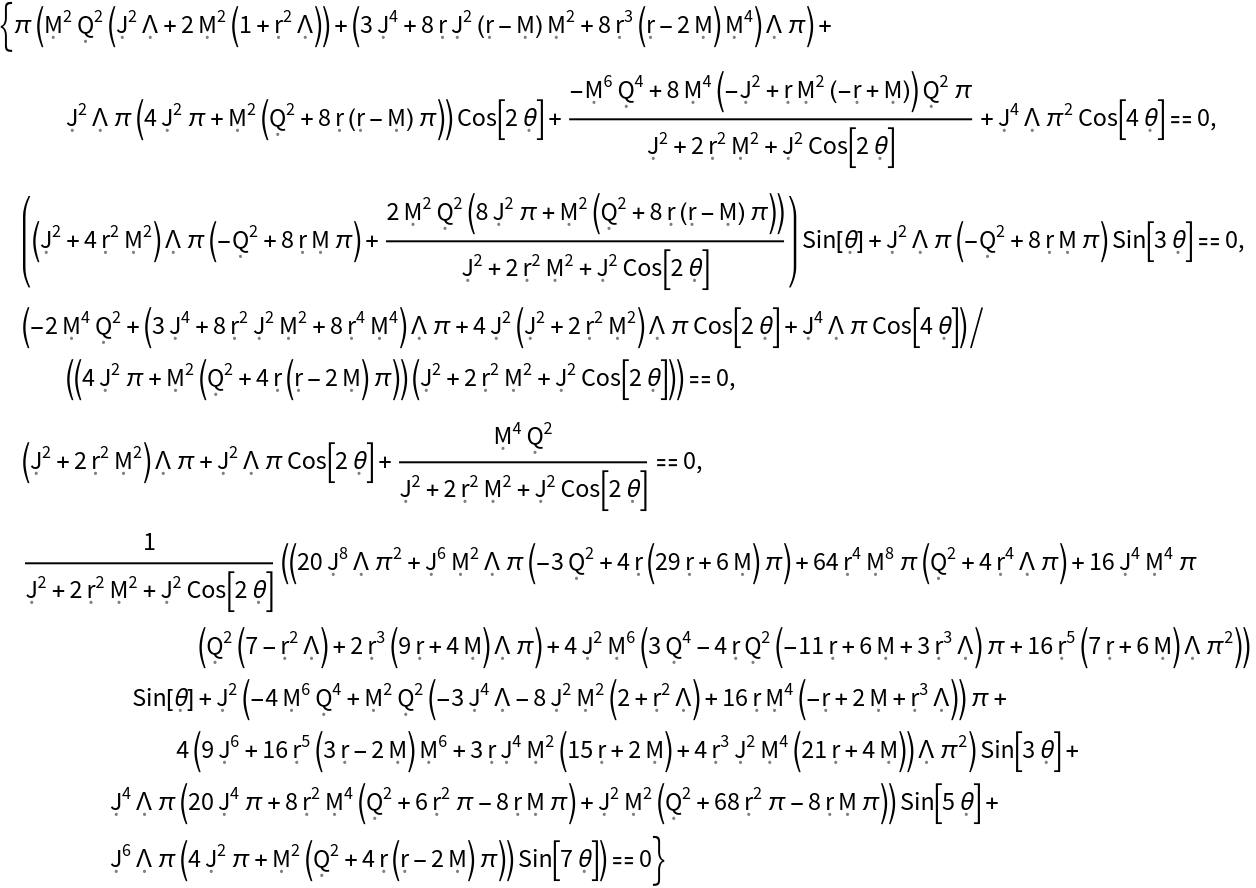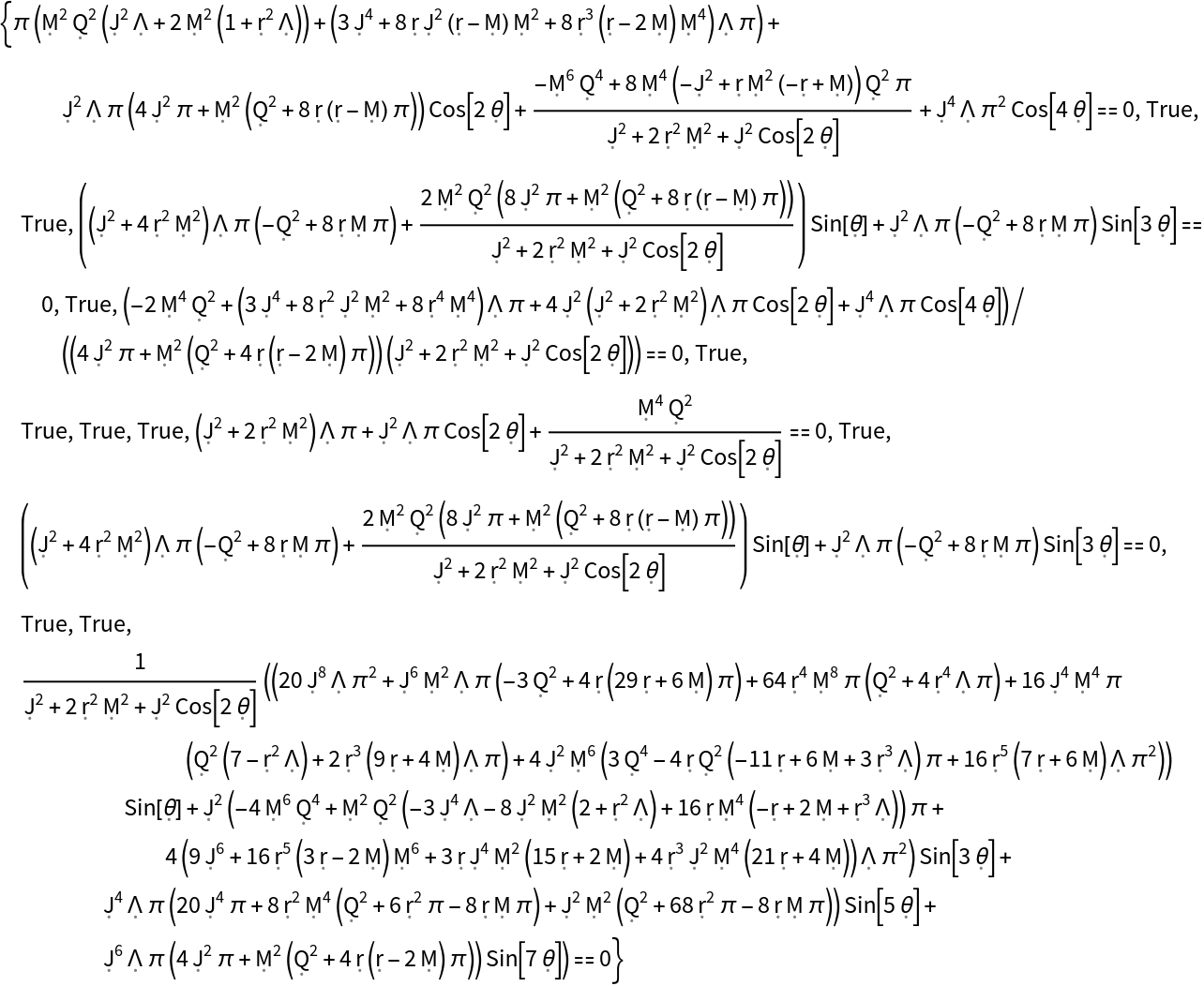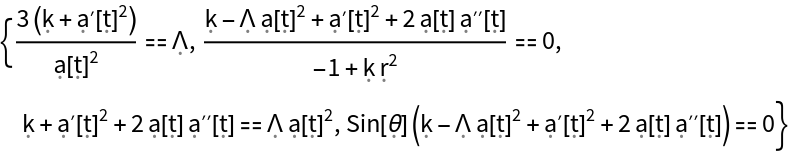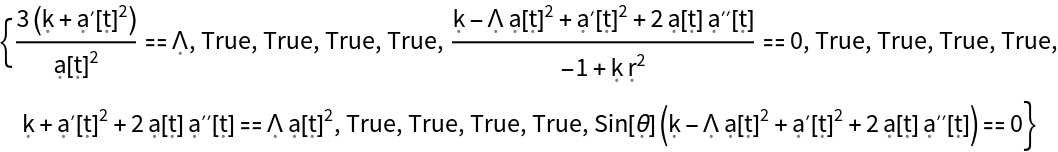Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SolveVacuumEinsteinEquations

Source Notebook

Determine whether a given Riemannian or pseudo-Riemannian manifold is a solution to the vacuum Einstein field equations

Contributed by: Jonathan Gorard

ResourceFunction["SolveVacuumEinsteinEquations"][MetricTensor[…],cosmo]

attempts to solve the vacuum Einstein field equations for the given MetricTensor, assuming cosmological constant cosmo.

ResourceFunction["SolveVacuumEinsteinEquations"][MetricTensor[…]]

uses the default (symbolic) value "" as the cosmological constant.

Details

The vacuum Einstein field equations assert that the Einstein curvature tensor (or, more generally, the Einstein curvature tensor plus the metric tensor multiplied by a non-zero cosmological constant) vanishes identically. Since the Einstein curvature tensor is the trace reverse of the Ricci curvature tensor, the Einstein curvature tensor vanishes identically if and only if the Ricci curvature tensor vanishes identically.
In differential geometry, the significance of the vacuum Einstein field equations is that they can be used to characterize Einstein manifolds, i.e. Riemannian or pseudo-Riemannian manifolds for which the Ricci curvature tensor is proportional to the metric tensor. Einstein manifolds with zero cosmological constant are necessarily Ricci-flat (due to the above trace reverse relationship between the two curvature tensors).
In general relativity, the significance of the vacuum Einstein field equations is that, by the full Einstein field equations, the Einstein curvature tensor (plus the metric tensor multiplied by a potentially non-zero cosmological constant) vanishes identically if and only if the stress-energy tensor, and hence the matter-energy content of spacetime, vanishes identically. It is for this reason that such solutions are known as vacuum (or sometimes lambdavacuum, in the case of non-zero cosmological constant) solutions.
ResourceFunction["SolveVacuumEinsteinEquations"] assumes a non-zero cosmological constant (represented by the purely symbolic value "") by default, although this can be overridden as part of the second argument of the function.
ResourceFunction["SolveVacuumEinsteinEquations"] classifies all vacuum solutions as either exact (i.e. no additional assumptions required) or non-exact (i.e. some additional assumptions required), depending upon whether any additional field equations must be assumed in order for the given MetricTensor to constitute a valid solution to the vacuum Einstein field equations. Any such field equations (if they exist) can be computed using the property "FieldEquations".
ResourceFunction["SolveVacuumEinsteinEquations"] does not assume any particular number of dimensions, nor any particular metric convention, for the underlying manifold (although some properties, such as "LorentzianConditions", implicitly assume a (-,+,+,+,…) signature). ResourceFunction["SolveVacuumEinsteinEquations"] also does not require the metric to be strictly symmetric (i.e. spin and torsion connections are also supported), although the computation of the Einstein curvature tensor implicitly assumes the torsion-free Levi-Civita connection by default.
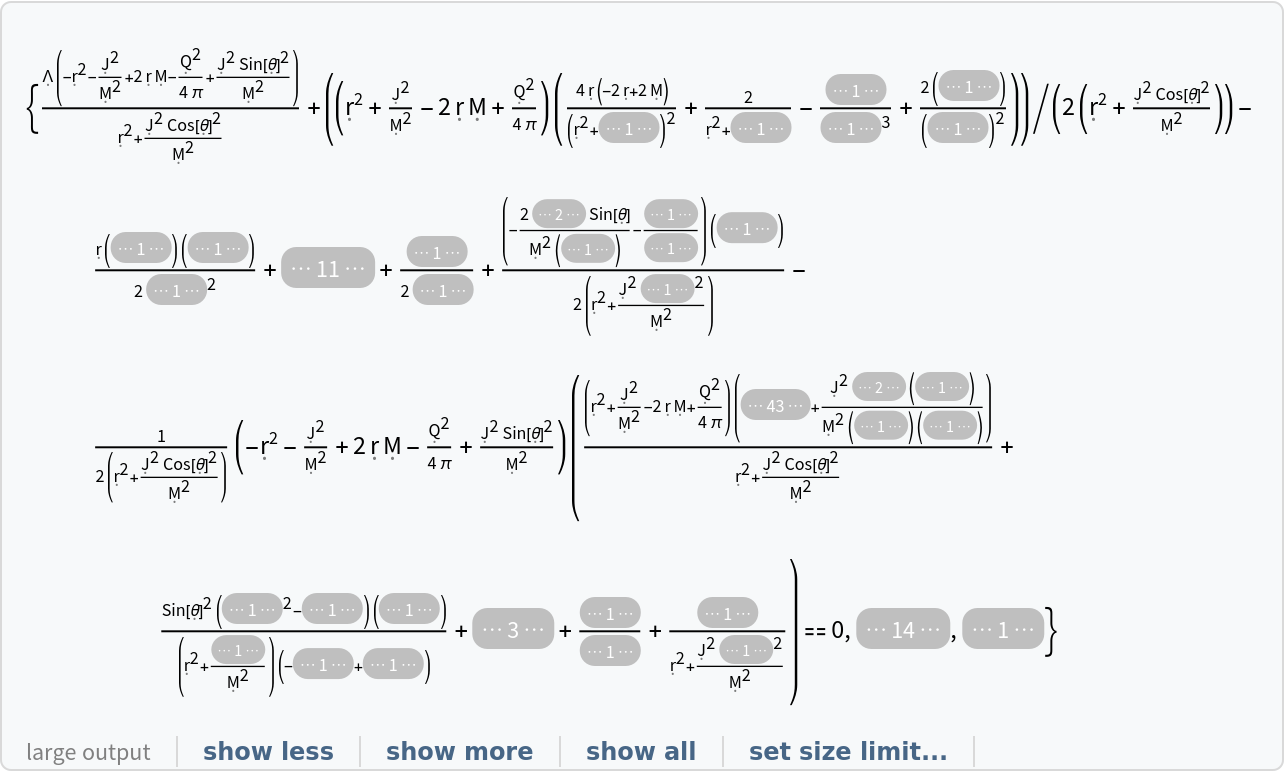
ResourceFunction["SolveVacuumEinsteinEquations"] implicitly keeps track of all known algebraic equivalences between tensor expressions, and can apply them for simplification purposes where necessary. Requesting the "ReducedEinsteinEquations" property has the effect of applying all known tensor equivalences and simplifying (note that this can have the effect of increasing computation time significantly).
By default, ResourceFunction["SolveVacuumEinsteinEquations"] evaluates all partial derivatives of the metric tensor automatically. In certain cases, however, these partial derivatives may be difficult or even impossible to compute, in which case the evaluation may not terminate in a reasonable time. Requesting the "SymbolicEinsteinEquations" property has the effect of leaving all partial derivatives unevaluated instead (note that this can have the effect of increasing expression length significantly).
If ResourceFunction["SolveVacuumEinsteinEquations"] succeeds in solving the vacuum Einstein field equations (or in proving that no such solution can exist), it will return a VacuumSolution expression.
Based on the eigenvalues of the matrix representation of the underlying metric tensor in covariant form, the underlying manifold will be classified by ResourceFunction["SolveVacuumEinsteinEquations"] as either Riemannian (all eigenvalues positive or all eigenvalues negative), pseudo-Riemannian (some eigenvalues positive and some eigenvalues negative), Lorentzian (all eigenvalues positive except for one negative, or all eigenvalues negative except for one positive) or Indeterminate.
The property "RiemannianConditions" returns the conditions necessary to guarantee that the eigenvalues of the matrix representation of the underlying metric tensor are strictly positive; "PseudoRiemannianConditions" returns the conditions necessary to guarantee that the eigenvalues of the matrix representation of the underlying metric tensor are all non-zero; "LorentzianConditions" returns the conditions necessary to guarantee that the eigenvalue corresponding to the {1,0,0,…} eigenvector of the underlying metric tensor (if it exists) is negative, with all other eigenvalues being positive. Note that this is strictly less general than the behavior of properties such as "RiemannianQ" (described in the point above), since it assumes certain features of the metric signature.
In VacuumSolution, the following properties are supported:
"FieldEquations"list of any (additional) field equations that must be assumed in order for the metric to be a valid solution to the vacuum Einstein field equations
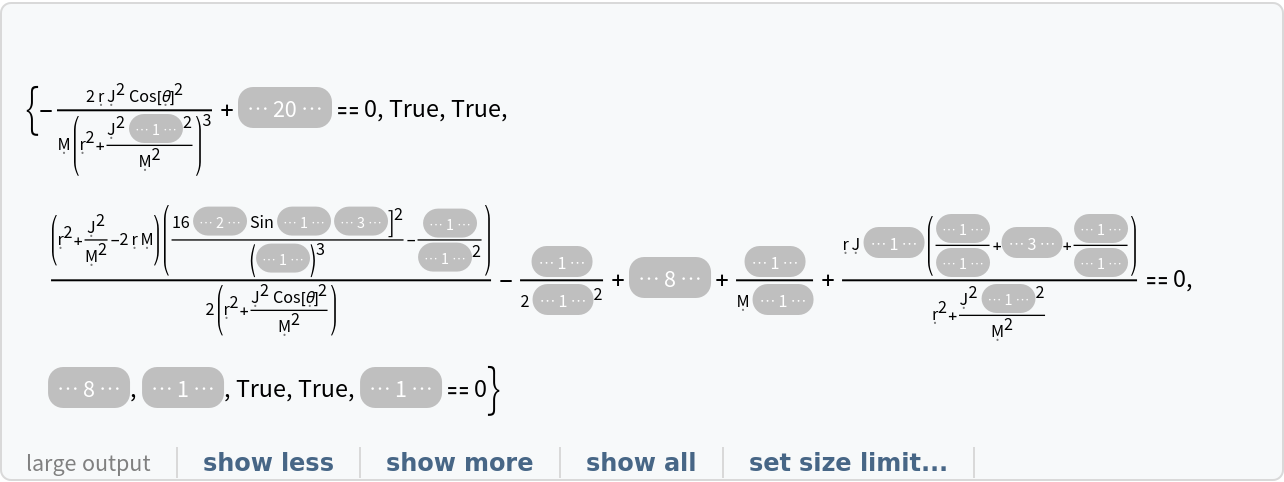
"EinsteinEquations"list of vacuum Einstein field equations asserting that the Einstein tensor (plus the metric tensor multiplied by the cosmological constant) is identically zero
"ReducedEinsteinEquations"list of vacuum Einstein field equations asserting that the Einstein tensor (plus the metric tensor multiplied by the cosmological constant) is identically zero, modulo all tensor equivalences
"SymbolicEinsteinEquatons"list of vacuum Einstein field equations asserting that the Einstein tensor (plus the metric tensor multiplied by the cosmological constant) is identically zero, with purely symbolic partial derivative operators
"MetricTensor"underlying metric tensor associated to the vacuum solution
"Coordinates"list of coordinate symbols for the vacuum solution
"CoordinateOneForms"list of differential 1-form symbols for the coordinates of the vacuum solution
"SolutionQ"whether the metric tensor is a valid solution to the vacuum Einstein field equations
"ExactSolutionQ"whether the metric tensor is a valid exact solution to the vacuum Einstein field equations (i.e. no additional field equations need to be assumed)
"CosmologicalConstant"value of the cosmological constant for the vacuum solution
"Dimensions"number of dimensions of the underlying manifold/spacetime described by the vacuum solution
"Signature"list of +1s and -1s designating the signature of the underlying manifold described by the vacuum solution (+1 for each positive eigenvalue of the metric, -1 for each negative eigenvalue of the metric)
"RiemannianQ"whether the underlying manifold described by the vacuum solution is Riemannian (i.e. all eigenvalues of the metric have the same sign)
"PseudoRiemannianQ"whether the underlying manifold described by the vacuum solution is pseudo-Riemannian (i.e. all eigenvalues of the metric are non-zero, but not all have the same sign)
"LorentzianQ"whether the underlying manifold described by the vacuum solution is Lorentzian (i.e. all eigenvalues of the metric have the same sign, except for one eigenvalue which has the opposite sign)
"RiemannianConditions"list of conditions required to guarantee that the underlying manifold described by the vacuum solution is Riemannian (i.e. all eigenvalues of the metric are positive)
"PseudoRiemannianConditions"list of conditions required to guarantee that the underlying manifold described by the vacuum solution is pseudo-Riemannian (i.e. all eigenvalues of the metric are non-zero)
"LorentzianConditions"list of conditions required to guarantee that the underlying manifold described by the vacuum solution is Lorentzian (i.e. the "time" eigenvalue of the metric is negative and all other eigenvalues are positive)
"Properties"list of properties

Examples

Basic Examples (2) 

Show that the Schwarzschild metric (e.g. for an uncharged, non-rotating black hole with symbolic mass "M") in standard spherical polar coordinates is a valid solution to the vacuum Einstein field equations with zero cosmological constant:

In[1]:=
metric = ResourceFunction["MetricTensor"]["Schwarzschild"]
Out[1]=
In[2]:=
solution = ResourceFunction["SolveVacuumEinsteinEquations"][metric, 0]
Out[2]=
In[3]:=
solution["SolutionQ"]
Out[3]=

Show that the Schwarzschild solution is exact (i.e. no additional field equations need to be assumed):

In[4]:=
solution["ExactSolutionQ"]
Out[4]=
In[5]:=
solution["FieldEquations"]
Out[5]=

Show that the Schwarzschild metric is not a valid solution to the vacuum Einstein field equations assuming a non-zero (symbolic) cosmological constant "":

In[6]:=
solution2 = ResourceFunction["SolveVacuumEinsteinEquations"][metric]
Out[6]=
In[7]:=
solution2["SolutionQ"]
Out[7]=
In[8]:=
solution2["CosmologicalConstant"]
Out[8]=

Show that the Kerr metric (e.g. for an uncharged, spinning black hole with symbolic mass "M" and symbolic angular momentum "J") in Boyer-Lindquist/oblate spheroidal coordinates is also a valid (exact) solution to the Einstein field equations with zero cosmological constant:

In[9]:=
metric2 = ResourceFunction["MetricTensor"]["Kerr"]
Out[9]=
In[10]:=
solution3 = ResourceFunction["SolveVacuumEinsteinEquations"][metric2, 0]
Out[10]=
In[11]:=
solution3["SolutionQ"]
Out[11]=
In[12]:=
solution3["ExactSolutionQ"]
Out[12]=

Show the list of all vacuum Einstein field equations, asserting that the Einstein curvature tensor for the Kerr geometry is identically zero:

In[13]:=
solution3["EinsteinEquations"]
Out[13]=

Show the list of all vacuum Einstein field equations for the Kerr geometry, with all algebraic equivalences imposed, and confirm that they hold identically:

In[14]:=
solution3["ReducedEinsteinEquations"]
Out[14]=

Find the conditions under which the Friedman-Lemaître-Robertson-Walker (FLRW) metric (for a homogeneous, isotropic and uniformly-expanding/contracting universe, with symbolic curvature parameter "k" and symbolic scale factor "a") in standard spherical polar coordinates is a valid solution to the vacuum Einstein field equations with symbolic cosmological constant "":

In[15]:=
metric = ResourceFunction["MetricTensor"]["FLRW"]
Out[15]=
In[16]:=
solution = ResourceFunction["SolveVacuumEinsteinEquations"][metric]
Out[16]=
In[17]:=
solution["FieldEquations"]
Out[17]=

Find the corresponding conditions for the case of zero cosmological constant:

In[18]:=
solution2 = ResourceFunction["SolveVacuumEinsteinEquations"][metric, 0]
Out[18]=
In[19]:=
solution2["FieldEquations"]
Out[19]=

Show that in neither case is the solution exact (i.e. additional field equations must be assumed):

In[20]:=
solution["ExactSolutionQ"]
Out[20]=
In[21]:=
solution2["ExactSolutionQ"]
Out[21]=

Find the conditions under which the Kerr-Newman metric (e.g. for a charged, spinning black hole with symbolic mass "M", symbolic angular momentum "J" and symbolic electric charge "Q") in Boyer-Lindquist/oblate spheroidal coordinates is also a valid (non-exact) solution to the vacuum Einstein field equations with symbolic cosmological constant "":

In[22]:=
metric2 = ResourceFunction["MetricTensor"]["KerrNewman"]
Out[22]=
In[23]:=
solution3 = ResourceFunction["SolveVacuumEinsteinEquations"][metric2]
Out[23]=
In[24]:=
solution3["FieldEquations"]
Out[24]=

Show the list of all vacuum Einstein field equations, asserting that the Einstein curvature tensor (plus the metric tensor multiplied by the cosmological constant) for the Kerr-Newman geometry is identically zero:

In[25]:=
solution3["EinsteinEquations"]
Out[25]=

Show the list of all vacuum Einstein field equations for the Kerr-Newman geometry, with all algebraic equivalences imposed, and confirm that they do not all hold identically (without additional assumptions):

In[26]:=
solution3["ReducedEinsteinEquations"]
Out[26]=
In[27]:=
solution3["ExactSolutionQ"]
Out[27]=

Scope (2) 

By default, SolveVacuumEinsteinEquations will use a symbolic value ("") for the cosmological constant:

In[28]:=
metric = ResourceFunction["MetricTensor"]["Godel"]
Out[28]=
In[29]:=
solution = ResourceFunction["SolveVacuumEinsteinEquations"][metric]
Out[29]=
In[30]:=
solution["CosmologicalConstant"]
Out[30]=
In[31]:=
solution["FieldEquations"]
Out[31]=

This default choice may be overridden using a second argument:

In[32]:=
solution2 = ResourceFunction["SolveVacuumEinsteinEquations"][metric, 0]
Out[32]=
In[33]:=
solution2["SolutionQ"]
Out[33]=

Solve the vacuum Einstein field equations for the FLRW metric, with symbolic curvature parameter "k" and symbolic scale factor "a", and assuming symbolic cosmological constant "":

In[34]:=
metric = ResourceFunction["MetricTensor"]["FLRW"]
Out[34]=
In[35]:=
solution = ResourceFunction["SolveVacuumEinsteinEquations"][metric]
Out[35]=

Show the list of properties:

In[36]:=
solution["Properties"]
Out[36]=

Show the list of (additional) field equations that must be assumed in order for the metric to be a valid solution to the vacuum Einstein field equations:

In[37]:=
solution["FieldEquations"]
Out[37]=

Show the list of vacuum Einstein field equations asserting that the Einstein curvature tensor (plus the metric tensor multiplied by the cosmological constant) must vanish identically:

In[38]:=
solution["EinsteinEquations"]
Out[38]=

Show the list of vacuum Einstein field equations asserting that the Einstein curvature tensor (plus the metric tensor multiplied by the cosmological constant) must vanish identically, with all algebraic equivalences imposed:

In[39]:=
solution["ReducedEinsteinEquations"]
Out[39]=

Show the list of vacuum Einstein field equations asserting that the Einstein curvature tensor (plus the metric tensor multiplied by the cosmological constant) must vanish identically, with all partial derivative operators left purely symbolic:

In[40]:=
solution["SymbolicEinsteinEquations"]
Out[40]=

Show the metric tensor for the underlying manifold represented by the vacuum solution:

In[41]:=
solution["MetricTensor"]
Out[41]=

Show the list of coordinate symbols for the vacuum solution:

In[42]:=
solution["Coordinates"]
Out[42]=

Show the list of differential 1-form symbols for the coordinates of the vacuum solution:

In[43]:=
solution["CoordinateOneForms"]
Out[43]=

Determine whether the metric tensor is a valid solution to the vacuum Einstein field equations:

In[44]:=
solution["SolutionQ"]
Out[44]=

Determine whether the metric tensor is a valid exact solution to the vacuum Einstein field equations (i.e. no additional field equations need to be assumed):

In[45]:=
solution["ExactSolutionQ"]
Out[45]=

Show the value of the cosmological constant for the vacuum solution:

In[46]:=
solution["CosmologicalConstant"]
Out[46]=

Show the number of dimensions of the underlying manifold represented by the vacuum solution:

In[47]:=
solution["Dimensions"]
Out[47]=

Show the signature of the underlying manifold represented by the vacuum solution (with +1s representing positive eigenvalues and -1s representing negative eigenvalues of the metric tensor):

In[48]:=
solution["Signature"]
Out[48]=

Determine whether the underlying manifold represented by the vacuum solution is Riemannian (i.e. all eigenvalues of the metric tensor have the same sign):

In[49]:=
solution["RiemannianQ"]
Out[49]=

Determine whether the underlying manifold represented by the vacuum solution is pseudo-Riemannian (i.e. all eigenvalues are non-zero, but not all have the same sign):

In[50]:=
solution["PseudoRiemannianQ"]
Out[50]=

Determine whether the underlying manifold represented by the vacuum solution is Lorentzian (i.e. all eigenvalues of the metric tensor have the same sign, except for one eigenvalue which has the opposite sign):

In[51]:=
solution["LorentzianQ"]
Out[51]=

Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the vacuum solution is Riemannian (i.e. all eigenvalues of the metric tensor are positive):

In[52]:=
solution["RiemannianConditions"]
Out[52]=

Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the vacuum solution is pseudo-Riemannian (i.e. all eigenvalues of the metric tensor are non-zero):

In[53]:=
solution["PseudoRiemannianConditions"]
Out[53]=

Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the vacuum solution is Lorentzian (i.e. the "time" eigenvalue is negative, and all other eigenvalues are positive):

In[54]:=
solution["LorentzianConditions"]
Out[54]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 27 February 2023

Source Metadata

  • Citation:
    • Charles W. Misner, Kip S. Thorne and John Archibald Wheeler (1973), Gravitation
    • Stephen Wolfram (2002), A New Kind of Science
    • Stephen Wolfram (2020), "A Class of Models with Potential to Represent Fundamental Physics"
    • Jonathan Gorard (2020), "Some Relativistic and Gravitational Properties of the Wolfram Model"
    • Jonathan Gorard (2020), "Some Quantum Mechanical Properties of the Wolfram Model"

Related Resources

License Information