Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Solve a sudoku puzzle
ResourceFunction["SolveSudokuPuzzle"][mat] solves a sudoku puzzle with the input mat specified by a SparseArray matrix. |
Solve a standard Sudoku puzzle:
| In[1]:= | ![solvedPuzzle = ResourceFunction["SolveSudokuPuzzle"][
puzzle = SparseArray[{{1, 3} -> 5, {1, 4} -> 3, {2, 1} -> 8, {2, 8} -> 2, {
3, 2} -> 7, {3, 5} -> 1, {3, 7} -> 5, {4, 1} -> 4, {4, 6} -> 5, {4, 7} -> 3, {5, 2} -> 1, {5, 5} -> 7, {5, 9} -> 6, {
6, 3} -> 3, {6, 4} -> 2, {6, 8} -> 8, {7, 2} -> 6, {7, 4} -> 5, {7, 9} -> 9, {8, 3} -> 4, {8, 8} -> 3, {9, 6} -> 9, {
9, 7} -> 7}, {9, 9}, _]];
Grid[#, Sequence[Dividers -> Table[{
Prepend[
Table[True, 2],
Thickness[2]]}, 2], Background -> {Automatic, Automatic,
Flatten[
Table[{i, j} -> If[
EvenQ[
Apply[Plus,
Floor[{i - 1, j - 1}/3]]],
Darker[White, 0.2], White], {i, 9}, {j, 9}]]}]] & /@ {puzzle, solvedPuzzle}](https://www.wolframcloud.com/obj/resourcesystem/images/095/095199c9-9249-4421-b86f-e92e6d3b1d89/4b526e14b18dd02c.png) |
| Out[2]= | 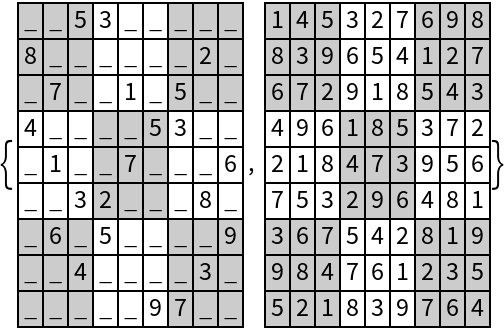 |
Solve a 16⨯16 Sudoku puzzle:
| In[3]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/6dfce4ba-4a15-4410-8804-8e727b9c5fa3"]](https://www.wolframcloud.com/obj/resourcesystem/images/095/095199c9-9249-4421-b86f-e92e6d3b1d89/1b12bb2479fedaf9.png) |
| Out[4]= | 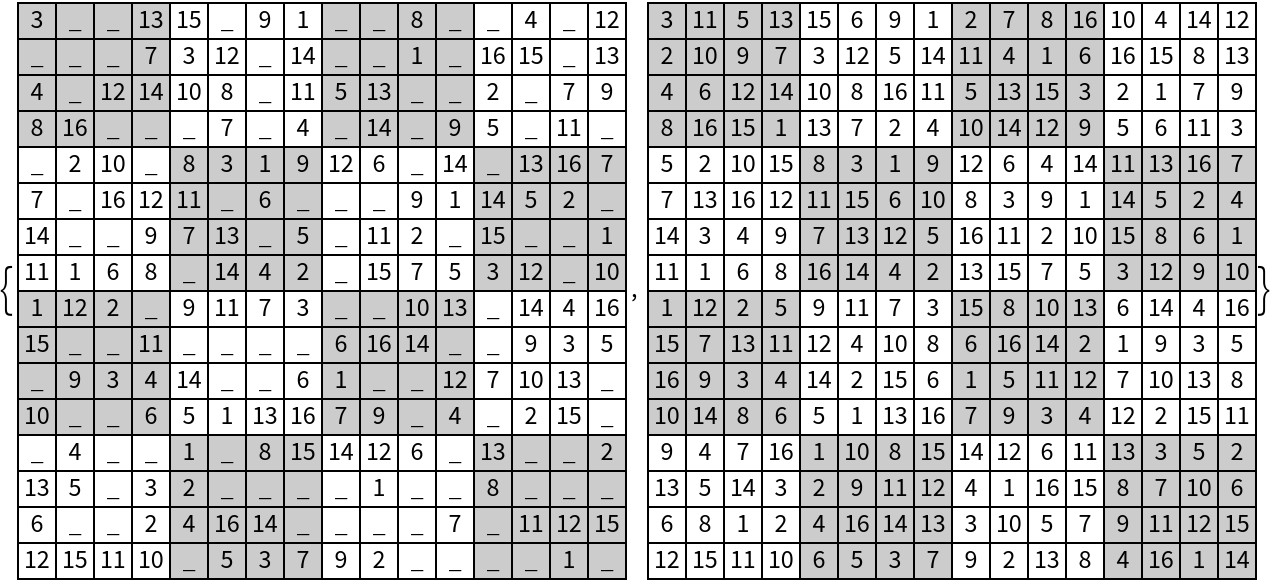 |
Generate a full standard Sudoku board by specifying the diagonal elements:
| In[5]:= |
| Out[5]= |  |
Generate a full 16⨯16 Sudoku board by randomly specifying the first column:
| In[6]:= | ![Grid[ResourceFunction["SolveSudokuPuzzle"][
SparseArray[
Thread[Thread[{Range[16], 1}] -> RandomSample[Range[16]]], {16, 16}]], Sequence[Dividers -> Table[{
Prepend[
Table[True, 3],
Thickness[2]]}, 2], Background -> {Automatic, Automatic,
Flatten[
Table[{i, j} -> If[
EvenQ[
Apply[Plus,
Floor[(1/4) {i - 1, j - 1}]]],
Darker[White, 0.2], White], {i, 16}, {j, 16}]]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/095/095199c9-9249-4421-b86f-e92e6d3b1d89/01fd97fe2e0868d3.png) |
| Out[6]= | 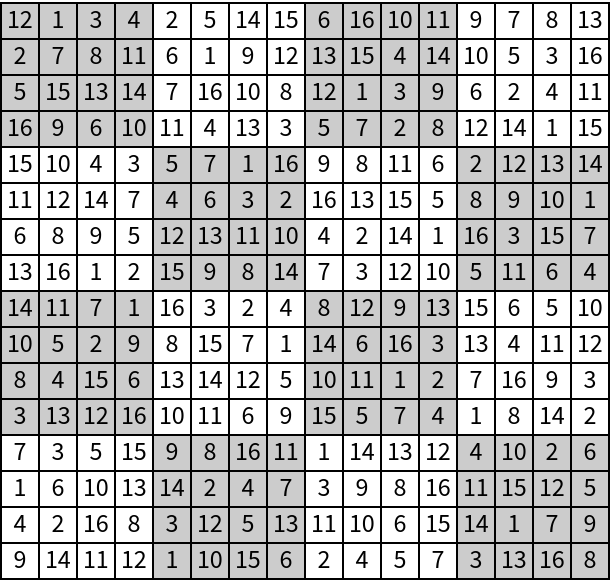 |
Generate a Sudoku board by specifying elements that cannot exist at certain positions:
| In[7]:= |
| Out[7]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License