Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Solve a killer sudoku puzzle
ResourceFunction["SolveKillerSudokuPuzzle"][pos,vals] solves a killer sudoku puzzle based on the position pos of cages and the values vals associated with the cages. |
Solve the following killer sudoku puzzle:
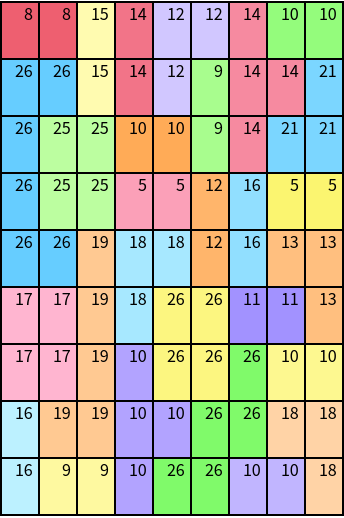
| In[1]:= | ![{cagePos, cageVals} = { {{{1, 1}, {1, 2}}, {{1, 4}, {2, 4}}, {{1, 7}, {2, 7}, {2, 8}, {3, 7}}, {{4, 4}, {4, 5}}, {{6, 1}, {6, 2}, {7, 1}, {
7, 2}}, {{6, 7}, {6, 8}}, {{7, 4}, {8, 4}, {8, 5}, {9, 4}}, {{9, 7}, {9, 8}}, {{1, 5}, {1, 6}, {2, 5}}, {{2, 1}, {2, 2}, {3, 1}, {
4, 1}, {5, 1}, {5, 2}}, {{2, 9}, {3, 8}, {3, 9}}, {{4, 7}, {5, 7}}, {{5, 4}, {5, 5}, {6, 4}}, {{8, 1}, {9, 1}}, {{7, 7}, {8, 6}, {8, 7}, {9, 5}, {9, 6}}, {{1, 8}, {1, 9}}, {{2, 6}, {3, 6}}, {{3, 2}, {3, 3}, {4, 2}, {4, 3}}, {{4, 8}, {4, 9}}, {{6, 5}, {6, 6}, {7, 5}, {7, 6}}, {{7, 8}, {7, 9}}, {{9, 2}, {9, 3}}, {{1, 3}, {2, 3}}, {{3, 4}, {3, 5}}, {{4, 6}, {5, 6}}, {{5, 8}, {5, 9}, {6, 9}}, {{5, 3}, {6, 3}, {7, 3}, {8, 2}, {8, 3}}, {{
8, 8}, {8, 9}, {9, 9}}}, {8, 14, 14, 5, 17, 11, 10, 10, 12, 26, 21, 16, 18, 16, 26, 10, 9, 25, 5, 26, 10, 9, 15, 10, 12, 13, 19, 18}};
solvedPuzzle = ResourceFunction["SolveKillerSudokuPuzzle"][cagePos, cageVals]](https://www.wolframcloud.com/obj/resourcesystem/images/6e9/6e974e0e-918b-4505-b61a-9ffee0e34a4d/52956f1861e4ec6e.png) |
| Out[2]= |
Display the solved puzzle:
| In[3]:= |
| Out[3]= |  |
The cage positions are a List of sublists where each sublist contains the positions within that cage:
| In[4]:= |  |
| Out[4]= |  |
The cage values are the sums of the numbers at each position in the cage:
| In[5]:= |
| Out[5]= |
Solve the puzzle:
| In[6]:= |
| Out[6]= |
See the solution:
| In[7]:= |
| Out[7]= |
This work is licensed under a Creative Commons Attribution 4.0 International License