Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Test whether the prime factors of an integer are less than a given threshold
ResourceFunction["SmoothIntegerQ"][p] represents an operator form of ResourceFunction["SmoothIntegerQ"] that can be applied to an integer. |
Show that 54 is 7-smooth:
| In[1]:= |
|
| Out[1]= |
|
54 is not 2-smooth, since its prime factors are 2 and 3:
| In[2]:= |
|
| Out[2]= |
|
The following is an operator which tests whether an integer is 7-smooth:
| In[3]:= |
|
| Out[3]= |
|
| In[4]:= |
|
| Out[4]= |
|
An integer is p-smooth for non-prime p if it is p-smooth for p being the greatest prime less than p:
| In[5]:= |
|
| Out[5]= |
|
π - smooth numbers are the same as 3-smooth numbers:
| In[6]:= |
![AllTrue[Table[
ResourceFunction["SmoothIntegerQ"][n, \[Pi]] == ResourceFunction["SmoothIntegerQ"][n, 3], {n, 1000}], TrueQ]](https://www.wolframcloud.com/obj/resourcesystem/images/14e/14e11308-823f-4dae-a4ce-9072a205c09e/4042a5a288780257.png)
|
| Out[6]= |
|
Print the 7-smooth numbers less than or equal to 100:
| In[7]:= |
|
| Out[7]= |
|
A negative integer is considered smooth if its absolute value is smooth:
| In[8]:= |
|
| Out[8]= |
|
Test that if n is 5-smooth, then so is -n for n up to 100:
| In[9]:= |
![AllTrue[Table[
ResourceFunction["SmoothIntegerQ"][n, 5] == ResourceFunction["SmoothIntegerQ"][-n, 5], {n, 100}], TrueQ]](https://www.wolframcloud.com/obj/resourcesystem/images/14e/14e11308-823f-4dae-a4ce-9072a205c09e/13d8d1b2cbf30cdd.png)
|
| Out[9]= |
|
Any input besides an integer in the first argument gives False:
| In[10]:= |
|
| Out[10]= |
|
| In[11]:= |
|
| Out[11]= |
|
Negative values for the second input always return False:
| In[12]:= |
|
| Out[12]= |
|
| In[13]:= |
|
| Out[13]= |
|
Calculate the number of "humble numbers" (7-smooth integers) with 1, 2, 3, 4 and 5 digits:
| In[14]:= |
![{"Digits\[Rule]Count",
Rule @@@ Tally[IntegerLength /@ Drop[Select[Range[10^5 - 1], ResourceFunction["SmoothIntegerQ"][7]], -1]] // Column} // Column](https://www.wolframcloud.com/obj/resourcesystem/images/14e/14e11308-823f-4dae-a4ce-9072a205c09e/615c827c80e09fbe.png)
|
| Out[14]= |
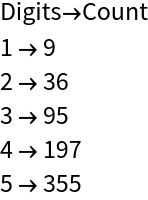
|
123200 and 123201 comprise the largest consecutive pair that are both 13-smooth:
| In[15]:= |
|
| Out[15]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License