Details
ResourceFunction["SkipListStructure"] is an implementation of a values-sorted association, which is optimized to have logarithmic
Insert and
KeyDrop times. In terms of functionality and design, this skiplist structure most closely follows
DataStructure (but without optimizations due to compiling code).
An initialization
init can be either an
Association or a
List. If the latter, the keys are taken to be the corresponding
Part indices.
ResourceFunction["SkipListStructure"] accepts the option
"OrderFunction", with default value
Order. User-specified alternatives should behave like built-in
Order by taking an adjacent pair of input values and returning 1 if the values are correctly ordered, -1 if they need to be transposed, or 0 if they are equivalent. An initialization of the structure can be done using this option.
In addition to primary usages above, ResourceFunction["SkipListStructure"] allows a wide variety of auxiliary usages:
| SkipListStructure[data, "InsertPosition", value] | searches data and returns before and after indices pointing where to insert value. |
| SkipListStructure[data, "Lookup", key,default] | attempts a Lookup, and returns default when key is not set. |
| SkipListStructure[data, "Normal", n] | returns a values-sorted Association of only those key-value pairs occurring on the nth level of the data structure. |
| SkipListStructure[data, "Last"] | returns the last element of data in the given ordering. |
| SkipListStructure[data, "PopLast"] | returns the last element and removes it from data. |
| SkipListStructure[data, "FirstLast"] | returns both first and last elements of data. |
| SkipListStructure[data, "MemberQ", value] | returns True if data already contains value, and False otherwise. |
| SkipListStructure[data, "EmptyQ"] | returns True if data contains no key-value pairs, and False otherwise. |
| SkipListStructure[data, "Validate"] | checks local structure and Ordering, returning True for valid data, and False otherwise. |
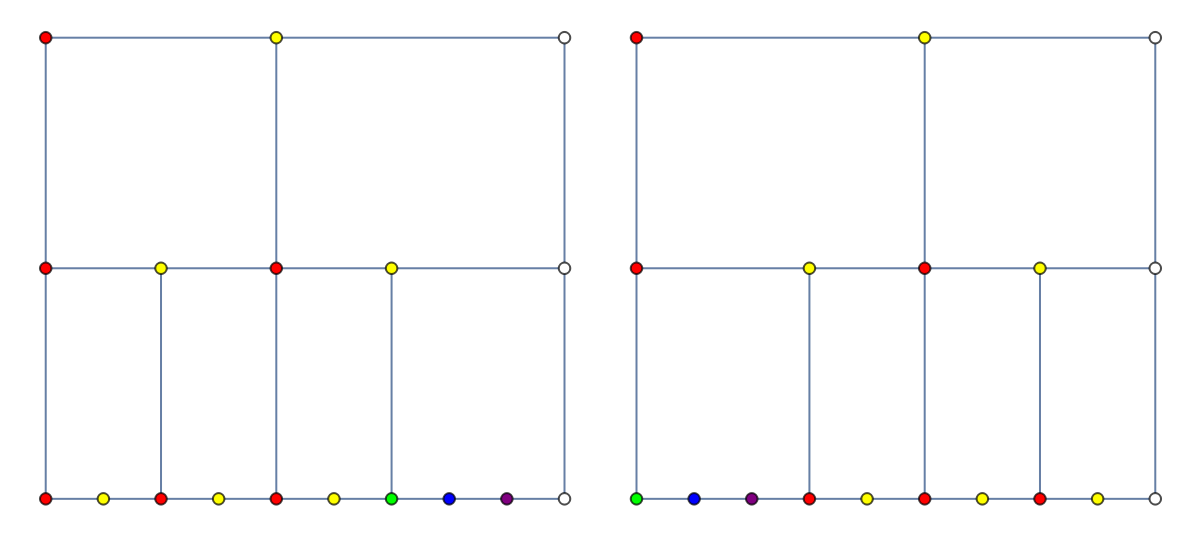
Desired complexity statistics are achieved by emulating 2,3-Trees with a linked list. In fact, the linked list has both horizontal and vertical links, so it can also be accurately described as a linked array with dimensions (log n)⨯ n.
All valid ResourceFunction["SkipListStructure"] linked arrays are consistent with a constraint on branching ratio per-level. One or two vertices occur between every pair of adjacent horizontal links.
The linked array of a particular ResourceFunction["SkipListStructure"] can be depicted through the "Visualization" method. Five or six different colors are used to distinguish between inequivalent vertex figures:
| Color | Vertical? | Next Color |
 | Yes |  |
 | No |  , , , or , or  |
 | Yes |  |
 | No |  |
 | No |  , , , or , or  |
 | Yes | None |
It is relatively easy to delete a blue or purple vertex, or to insert around a yellow vertex. Deleting a yellow vertex or inserting around a blue or purple vertex sometimes requires non-trivial recursion and heuristic decision making.
The leading depth dimension
log n is predictive of
Insert /
KeyDrop times. This method iterates through levels, making local changes only, until a halting condition is reached when the
ResourceFunction["SkipListStructure"] is proven valid around every vertex.
ResourceFunction["SkipListStructure"] is path dependent with regard to sequences of insertions and deletions. Two
ResourceFunction["SkipListStructure"] objects can fail a
SameQ test, while having the same normal form.
![If[ResourceFunction["SkipListStructure"][data, "Insert", 2, "alpha"],
ResourceFunction["SkipListStructure"][data, "Normal"]]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/57490dbfab3f1d45.png)
![If[ResourceFunction["SkipListStructure"][data, "KeyDrop", 2],
ResourceFunction["SkipListStructure"][data, "Normal"]]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/6e6d43018f5a2958.png)
![If[ResourceFunction["SkipListStructure"][data, "KeyDrop", 1],
ResourceFunction["SkipListStructure"][data, "EmptyQ"]]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/34ab97802271e9fd.png)
![SeedRandom[903274];
data = ResourceFunction["SkipListStructure"][RandomReal[1, 10]];
Table[ResourceFunction["SkipListStructure"][data, "PopFirst"], 10]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/64def85558bca2b9.png)
![SeedRandom[920384];
data = ResourceFunction["SkipListStructure"][
Association@MapIndexed[Rule[#2, #1] &,
RandomSample[WordList[], 30]]];
ResourceFunction["SkipListStructure"][data, "FirstLast"]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/0c34e566bfce8228.png)
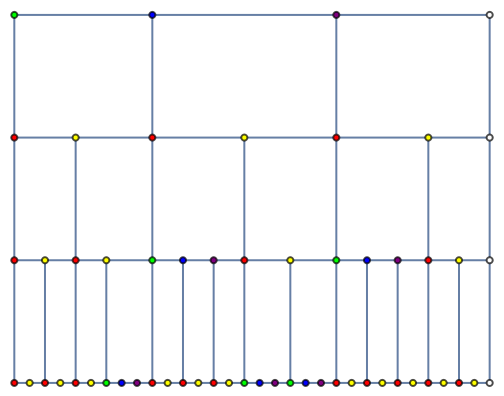
![SeedRandom[7348923];
data = ResourceFunction["SkipListStructure"][
Association@Map[Rule[Key[LetterNumber[#]], #] &,
RandomSample[Alphabet[]]]];
ResourceFunction["SkipListStructure"][data, "Visualization"]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/15dca9d1abb51ea8.png)

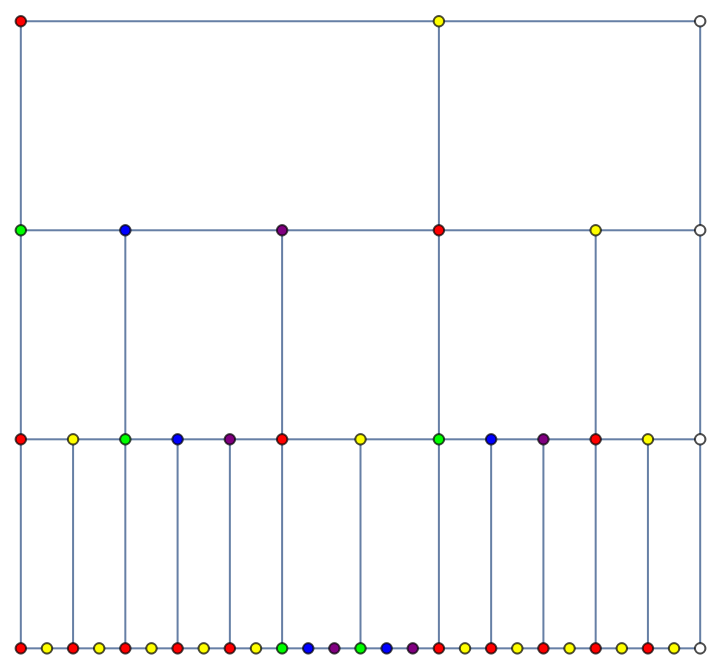
![data = ResourceFunction["SkipListStructure"][
RandomTree /@ RandomInteger[{1, 8}, 4]];
ResourceFunction["SkipListStructure"][data, "Normal"]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/2e5e52ed3d128cd6.png)

![SeedRandom[903274];
data = ResourceFunction["SkipListStructure"][RandomReal[1, 10],
"OrderFunction" -> Function[-Order[#1, #2]]];
Table[ResourceFunction["SkipListStructure"][data, "PopFirst"], 10]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/08f37c2be15b4c1a.png)
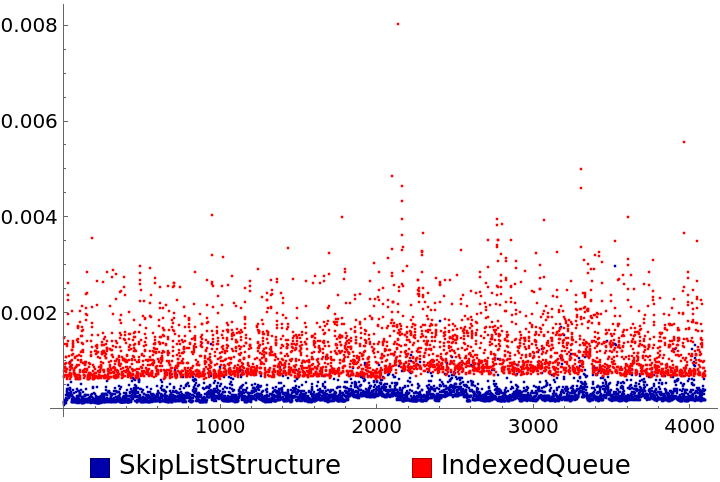
![Module[{randData, heap, heapTimes, data, skipTimes, size = 2^12},
SeedRandom[23434];
randData = MapIndexed[#2[[1]] -> #1 &,
RandomInteger[size, size]];
heap = ResourceFunction["IndexedQueue"][{
"InitialSize" -> 1, "NullElement" -> Missing[],
"ComparisonFunction" -> Greater}, {}, "Initialize"];
heapTimes = Reap[Module[{next}, Fold[Sow[AbsoluteTiming[
ResourceFunction["IndexedQueue"][heap, Last[#2], "Enqueue"]
][[1]]] &, {}, randData]]][[2, 1]];
data = ResourceFunction["SkipListStructure"][];
skipTimes = Reap[Fold[Sow[AbsoluteTiming[ ResourceFunction["SkipListStructure"][data, "Insert", First[#2], Last[#2]
]][[1]]] &, {}, randData]][[2, 1]];
Labeled[Show[
ListPlot[skipTimes, PlotStyle -> Darker@Blue],
ListPlot[heapTimes, PlotStyle -> Red], PlotRange -> All],
Row[{Darker@Blue, Text@" SkipListStructure",
Spacer[35], Red, Text@" IndexedQueue"}]
]
]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/6fb316633c4ec5fb.png)
![SeedRandom[903274];
data = ResourceFunction["SkipListStructure"][RandomReal[1, 10]];
Table[ResourceFunction["SkipListStructure"][data, "PopFirst"], 10]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/4403e70a8a746f67.png)

![ResourceFunction["SkipListStructure"][data, "GarbageCollect"];
SameQ[data, ResourceFunction["SkipListStructure"][]]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/7c2c2189a2f9236b.png)
![With[{data = ResourceFunction["SkipListStructure"][RandomReal[1, 10]]},
SameQ[ResourceFunction["SkipListStructure"][data, "Lookup", #] & /@ {2, 3},
ResourceFunction["SkipListStructure"][data, "Lookup", {2, 3}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/709e55391707efd3.png)
![GraphicsRow[ResourceFunction["SkipListStructure"][#,
"Visualization"] & /@ compareSkips]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d592d98-1c69-4efe-98ab-929d9112aa88/148507b7e71e045d.png)