Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SkewTridiagonalDecomposition

Source Notebook

Compute the skew-tridiagonal decomposition of an antisymmetric matrix

Contributed by: Wolfram Staff (original content by M. Wimmer)

ResourceFunction["SkewTridiagonalDecomposition"][m]

gives the skew-tridiagonal decomposition of antisymmetric matrix m.

Details and Options

The result is given in the form {q,t}, where q is a unitary matrix and t is a tridiagonal matrix such that m⩵q.t.qT.
Skew-symmetric matrices are also called antisymmetric.
ResourceFunction["SkewTridiagonalDecomposition"] is computed using Householder transformations.

Examples

Basic Examples (2) 

Construct a a skew-symmetric matrix:

In[1]:=
# - Transpose[#] &@RandomReal[1, {8, 8}]
Out[1]=

The skew-tridiagonal decomposition:

In[2]:=
{q, t} = ResourceFunction["SkewTridiagonalDecomposition"][%];
In[3]:=
MatrixForm /@ %
Out[3]=

Scope (2) 

The skew-tridiagonal decomposition of a real antisymmetric matrix:

In[4]:=
# - Transpose[#] &@RandomReal[1, {6, 6}]
Out[4]=
In[5]:=
MatrixForm /@ ResourceFunction["SkewTridiagonalDecomposition"][%]
Out[5]=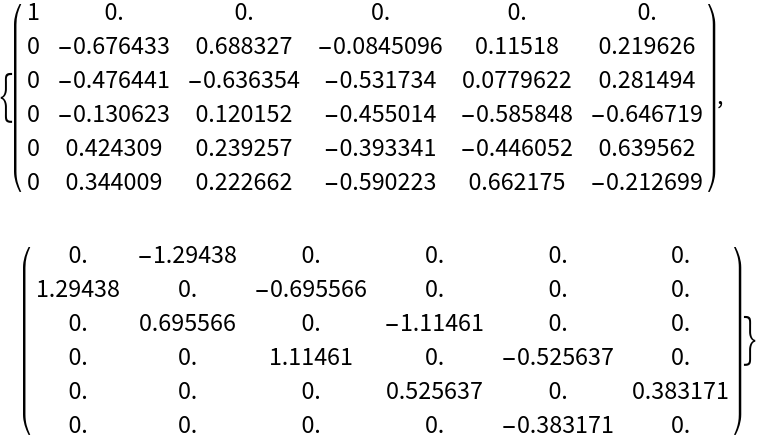

The skew-tridiagonal decomposition of a complex antisymmetric matrix:

In[6]:=
# - Transpose[#] &@RandomComplex[1 + I, {6, 6}]
Out[6]=
In[7]:=
ResourceFunction["SkewTridiagonalDecomposition"][%]
Out[7]=

Properties and Relations (4) 

Compute the Pfaffian of an antisymmetric matrix by reducing it to the tridiagonal form:

In[8]:=
m = # - Transpose[#] &@RandomComplex[1 + I, {6, 6}]
Out[8]=
In[9]:=
{q, t} = ResourceFunction["SkewTridiagonalDecomposition"][m];
In[10]:=
t // MatrixForm
Out[10]=
In[11]:=
PfaffianTridiagonal[m_] := Times @@ First /@ Partition[Diagonal[m, 1], UpTo[2]]
In[12]:=
PfaffianTridiagonal[t]
Out[12]=

Compare with the result of the resource function Pfaffian:

In[13]:=
ResourceFunction["Pfaffian"][m]^2 == %^2 == Det[m]
Out[13]=

In the result of {q,t}=SkewTridiagonalDecomposition[m], the matrix q is unitary and t is tridiagonal:

In[14]:=
m = # - Transpose[#] &@RandomComplex[1 + I, {3, 3}];
In[15]:=
{q, t} = ResourceFunction["SkewTridiagonalDecomposition"][m];
In[16]:=
UnitaryMatrixQ[q]
Out[16]=
In[17]:=
MatrixForm[t]
Out[17]=

The original matrix is given by q.t.Transpose[q]:

In[18]:=
m - q . t . Transpose[q] // Chop
Out[18]=

For real matrices, SkewTridiagonalDecomposition gives result similar to HessenbergDecomposition:

In[19]:=
m = # - Transpose[#] &@RandomReal[1, {6, 6}];
In[20]:=
{q, t} = ResourceFunction["SkewTridiagonalDecomposition"][m];
In[21]:=
{p, h} = HessenbergDecomposition[m];
In[22]:=
q - p // Chop
Out[22]=
In[23]:=
t - h // Chop
Out[23]=

The resource function SkewLTLDecomposition also produces a tridiagonal matrix t with the same Pfaffian, possibly up to the sign:

In[24]:=
m = # - Transpose[#] &@RandomReal[1, {6, 6}];
In[25]:=
{q, t} = ResourceFunction["SkewTridiagonalDecomposition"][m];
In[26]:=
t // MatrixForm
Out[26]=
In[27]:=
{l, t1, p} = ResourceFunction["SkewLTLDecomposition"][m];
In[28]:=
t1 // MatrixForm
Out[28]=
In[29]:=
Abs[ResourceFunction["Pfaffian"][m]] == Abs[ResourceFunction["Pfaffian"][t]] == Abs[ResourceFunction["Pfaffian"][t1]]
Out[29]=

Version History

  • 1.0.0 – 04 November 2020

Source Metadata

  • Citation:
    • Wimmer, M., "Algorithm 923: Efficient Numerical Computation of the Pfaffian for Dense and Banded Skew-Symmetric Matrices." ACM Trans. Math. Softw., vol. 38, no. 4, 1–17, 2012. DOI: 10.1145/2331130.2331138.

Related Resources

License Information