Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SkewLineSegment

Source Notebook

Get the shortest segment between skew lines

Contributed by: Ed Pegg Jr

ResourceFunction["SkewLineSegment"][j, k]

return the shortest segment between skew lines j and k as a 3D coordinate pair.

ResourceFunction["SkewLineSegment"][Line[j],Line[k]]

return the shortest segment between skew Line objects j and k as a Line segment.

Details

The lines j and k are both assumed to be specified as two 3D points.
The lines are assumed to be infinite lines. Skew segments {{1,0,0},{2,0,0}} and {{0,1,1},{0,2,1}} would return {{0,0,0},{0,0,1}} instead of the edge case {{1,0,0},{0,1,1}}.

Examples

Basic Examples (2) 

Find the shortest segment between two skew lines:

In[1]:=
line1 = {{3, 1, 4}, {1, 5, 9}}; line2 = {{2, 6, 5}, {3, 5, 8}}; dat = ResourceFunction["SkewLineSegment"][line1, line2]
Out[3]=

A list of lines may also be used:

In[4]:=
ResourceFunction["SkewLineSegment"][{line1, line2}]
Out[4]=

Show the lines and segment:

In[5]:=
Graphics3D[{InfiniteLine[line1], InfiniteLine[line2], Green, Line[dat]}, ImageSize -> Small]
Out[5]=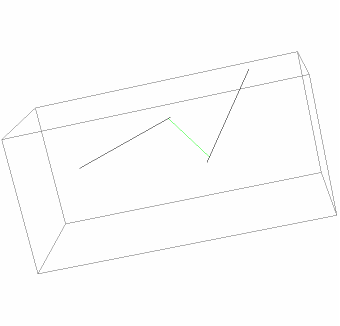

When two skew lines are Line objects, the returned segment is a Line:

In[6]:=
line1 = Line[{{2, 7, 1}, {8, 2, 8}}]; line2 = Line[{{1, 8, 2}, {8, 4, 5}}]; dat = ResourceFunction["SkewLineSegment"][line1, line2]
Out[7]=

Show the skew lines and shortest connecting segment:

In[8]:=
Graphics3D[{line1, line2, Green, dat}, ImageSize -> Small]
Out[8]=

Possible Issues (3) 

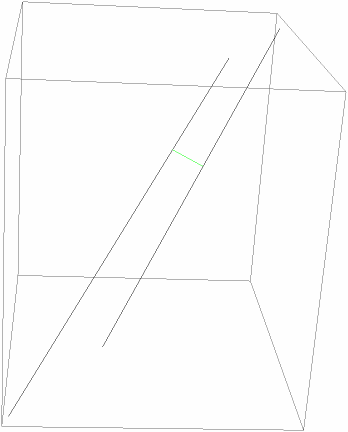If both lines are degenerate, the two points will be returned:

In[9]:=
line1 = {{1, 1, 1}, {1, 1, 1}}; line2 = {{2, 2, 2}, {2, 2, 2}}; dat = ResourceFunction["SkewLineSegment"][line1, line2]
Out[11]=

If one line is degenerate, the resource function PointLineDistance is used in order to return a segment:

In[12]:=
line1 = {{1, 1, 1}, {1, 1, 1}}; line2 = {{2, 2, 2}, {3, 4, 5}}; dat = ResourceFunction["SkewLineSegment"][line1, line2]
Out[14]=

If the lines are not skew, the resource function LineIntersection is used in order to return a degenerate segment:

In[15]:=
line1 = {{0, 0, 0}, {2, 2, 0}}; line2 = {{2, 0, 0}, {0, 2, 0}}; dat = ResourceFunction["SkewLineSegment"][line1, line2]
Out[16]=

Neat Examples (6) 

Find the skew line segments in a tetrahedron:

In[17]:=
tet = {{3, 1, 4}, {1, 5, 9}, {2, 6, 5}, {3, 5, 8}}; subs = Subsets[tet, {2}]; s1 = ResourceFunction["SkewLineSegment"][subs[[1]], subs[[6]]]; s2 = ResourceFunction["SkewLineSegment"][subs[[2]], subs[[5]]]; s3 = ResourceFunction["SkewLineSegment"][subs[[3]], subs[[4]]];

Repeat for two more layers:

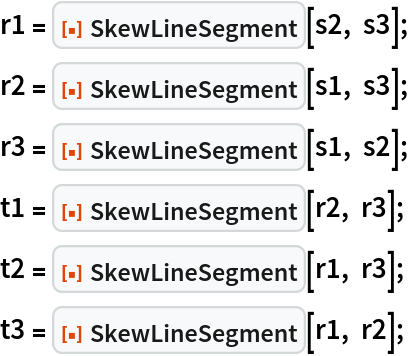
When plotted, the secondary and tertiary skew segments seem to make a closed cycle:

In[18]:=
Graphics3D[{Line /@ subs, Green, Line /@ {s1, s2, s3}, Red, Tube /@ {r1, r2, r3}, Blue, Tube /@ {t1, t2, t3}}, ImageSize -> Small]
Out[18]=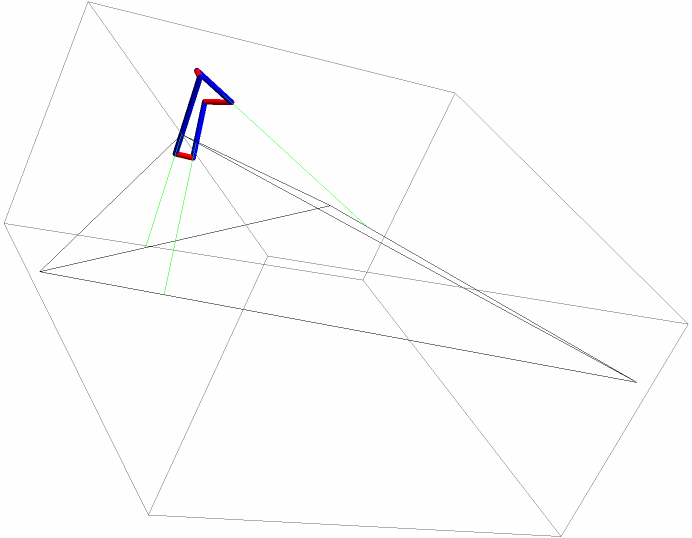

Check that a cycle exists:

In[19]:=
{r1, ResourceFunction["SkewLineSegment"][t2, t3]}
Out[19]=

Find the skew-cycle:

In[20]:=
skewcycle = First /@ FindCycle[Graph[UndirectedEdge @@@ {r1, r2, r3, t1, t2, t3}]][[1]]
Out[20]=

Show the skew-cycle:

In[21]:=
Graphics3D[{Tube /@ Partition[skewcycle, 2, 1, 1]}, ImageSize -> Small]
Out[21]=

Requirements

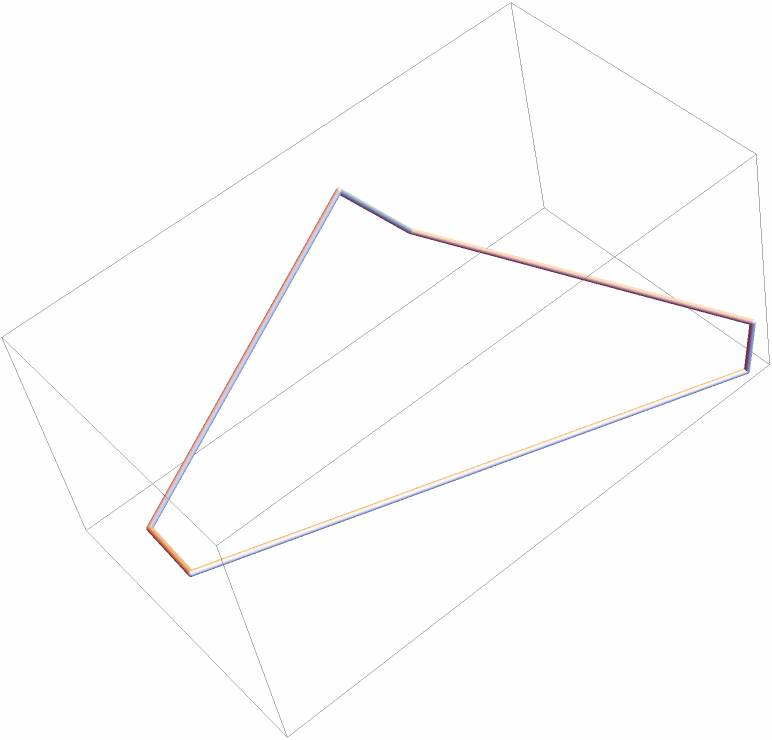Wolfram Language 12.0 (April 2019) or above

Version History

  • 1.0.0 – 14 June 2024

Related Resources

License Information