Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SimplexMeasure

Source Notebook

Get the measure of a simplex or simplicial complex

Contributed by: Richard Hennigan (Wolfram Research)

ResourceFunction["SimplexMeasure"][simplex]

gives the measure of simplex.

ResourceFunction["SimplexMeasure"][{simplex1,simplex2,…}]

gives the measure of the simplicial complex containing simplex1,simplex2,….

ResourceFunction["SimplexMeasure"][complex,d]

gives the d-dimensional measure of complex.

Details

A simplex can be specified by any of the following:
Point[v] a point
Line[{v1,v2}] a line segment
Triangle[{v1,v2,v3}] or Polygon[{v1,v2,v3}]a filled triangle
Tetrahedron[{v1,v2,v3,v4}] a filled tetrahedron
Simplex[{v1,v2,…,vn}] an n-1 dimensional simplex
A simplicial complex can be specified by any of the following:
{simplex1,simplex2,…} a list of simplices
{{v1,2,…,v1,n},{v2,2,…,v2,n},…} a list of lists of vertices
MeshRegion[…] a mesh region
BoundaryMeshRegion[…] a boundary mesh region
ResourceFunction["SimplexMeasure"] uses the Cayley-Menger determinant to compute the measure of simplices of arbitrary dimension.

Examples

Basic Examples (7) 

Get the measure of a Simplex:

In[1]:=
ResourceFunction["SimplexMeasure"][ Simplex[{{x1, y1}, {x2, y2}}]] // FullSimplify
Out[1]=

Compare to Euclidean distance:

In[2]:=
ResourceFunction["RealEuclideanDistance"][{x1, y1}, {x2, y2}]
Out[2]=

Get the measure of a Triangle:

In[3]:=
ResourceFunction["SimplexMeasure"][ Triangle[{{x1, y1}, {x2, y2}, {x3, y3}}]] // FullSimplify
Out[3]=

Compare to Area:

In[4]:=
Area[Triangle[{{x1, y1}, {x2, y2}, {x3, y3}}]]
Out[4]=

Get the measure of a random 100-dimensional Simplex:

In[5]:=
ResourceFunction["SimplexMeasure"][ Simplex[RandomReal[{-10, 10}, {101, 101}]]]
Out[5]=

Get the measure of a simplicial complex, represented as a list of simplices:

In[6]:=
ResourceFunction[ "SimplexMeasure"][{Simplex[{{x1, y1}, {x2, y2}}], Simplex[{{x3, y3}, {x4, y4}}]}]
Out[6]=

Get the measure of a simplicial complex, represented by lists of vertices:

In[7]:=
ResourceFunction[ "SimplexMeasure"][{{{0, 0}, {1, 0}}, {{0, 0}, {0, 1}}, {{1, 0}, {0, 1}}}]
Out[7]=

Specify a dimension to measure:

In[8]:=
complex = {Point[{x1, y1}], Line[{{x2, y2}, {x3, y3}}], Triangle[{{x4, y4}, {x5, y5}, {x6, y6}}]}
Out[8]=
In[9]:=
ResourceFunction["SimplexMeasure"][complex, 1] // FullSimplify
Out[9]=
In[10]:=
ResourceFunction["SimplexMeasure"][complex, 2] // FullSimplify
Out[10]=

Get the measure of a MeshRegion:

In[11]:=
mesh = MeshRegion[{{0, 0}, {1, 0}, {0, 1}, {1, 1}, {2, 1}, {2, 0}}, Simplex[{{1, 2, 3}, {4, 5, 6}}]]
Out[11]=
In[12]:=
ResourceFunction["SimplexMeasure"][mesh]
Out[12]=

Properties and Relations (7) 

The measure for Point corresponds to counts:

In[13]:=
points = Point /@ Tuples[Range[5], 2]
Out[13]=
In[14]:=
Graphics[points]
Out[14]=
In[15]:=
ResourceFunction["SimplexMeasure"][points]
Out[15]=

For mesh regions, SimplexMeasure is equivalent to RegionMeasure:

In[16]:=
mesh = ResourceData["Stanford Bunny", "MeshRegion"]
Out[16]=
In[17]:=
ResourceFunction["SimplexMeasure"][mesh]
Out[17]=
In[18]:=
RegionMeasure[mesh]
Out[18]=

SimplexMeasure works for arbitrary dimension:

In[19]:=
s = Table[Simplex[RandomReal[{-1, 1}, {n, n}]], {n, 5}]
Out[19]=
In[20]:=
ResourceFunction["SimplexMeasure"] /@ s
Out[20]=

Compare to RegionMeasure:

In[21]:=
RegionMeasure /@ s
Out[21]=

SimplexMeasure performs best when given lists of vertices as an array:

In[22]:=
array = RandomReal[{-1000, 1000}, {1000, 2, 2}]; lines = Simplex /@ array;
In[23]:=
RepeatedTiming[ResourceFunction["SimplexMeasure"][lines]]
Out[23]=
In[24]:=
RepeatedTiming[ResourceFunction["SimplexMeasure"][array]]
Out[24]=

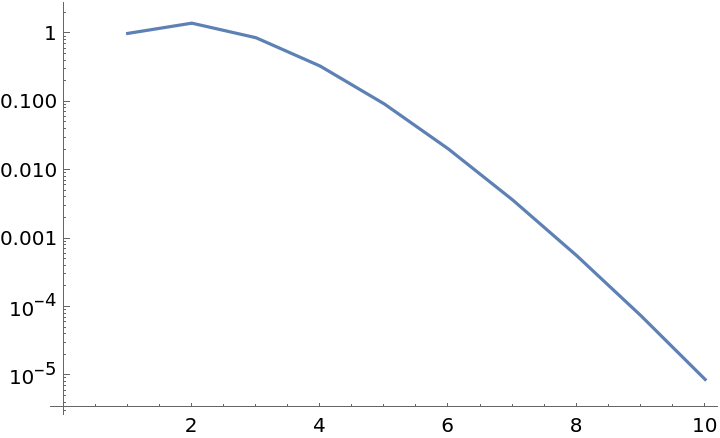
Get the measure of the first 10 standard simplices:

In[25]:=
Table[ResourceFunction["SimplexMeasure"][ ResourceFunction["StandardSimplex"][n]], {n, 0, 9}]
Out[25]=
In[26]:=
ListLogPlot[%, Joined -> True]
Out[26]=

Here’s the corresponding formula:

In[27]:=
Table[Sqrt[n + 1]/n!, {n, 0, 9}]
Out[27]=

SimplexMeasure uses more efficient methods for simplicial complexes below 6 dimensions:

In[28]:=
SeedRandom[1]; t = Table[ First[RepeatedTiming[ ResourceFunction["SimplexMeasure"][ RandomReal[{-5, 5}, {100, n, 12}]]]], {n, 2, 12}]
Out[26]=
In[29]:=
ListLogPlot[t, Joined -> True]
Out[29]=

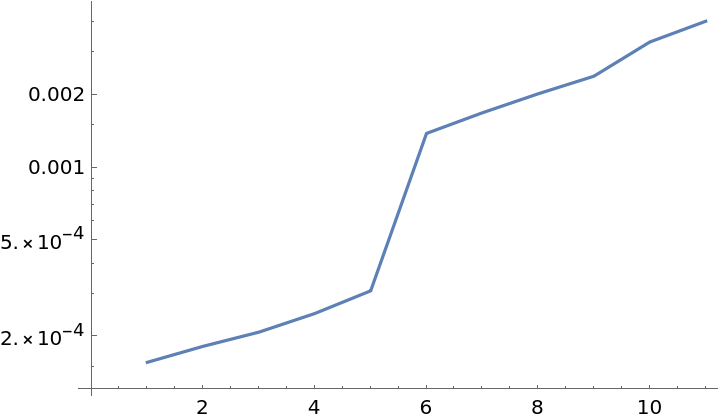
Measure a simplex and its boundary:

In[30]:=
simplex = Simplex[{{x1, y1}, {x2, y2}, {x3, y3}}]; Simplify[ResourceFunction["SimplexMeasure"][simplex], Reals]
Out[26]=
In[31]:=
boundary = ResourceFunction["SimplexBoundary"][simplex]
Out[31]=
In[32]:=
Simplify[ResourceFunction["SimplexMeasure"][boundary], Reals]
Out[32]=

Possible Issues (1) 

SimplexMeasure is not supported for abstract simplices:

In[33]:=
ResourceFunction["SimplexMeasure"][Simplex[{1, 2, 3}]]
Out[33]=
In[34]:=
ResourceFunction["SimplexBoundary"][Simplex[{1, 2, 3}]]
Out[34]=
In[35]:=
ResourceFunction["SimplexMeasure"][%]
Out[35]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.1 – 06 December 2021
  • 1.0.0 – 11 March 2019

Related Resources

License Information