Basic Examples (4)
Retrieve the ResourceFunction:
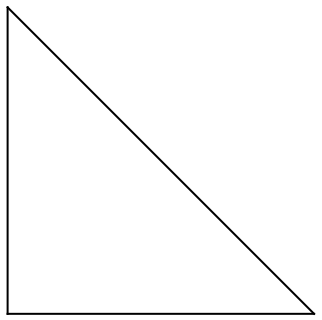
Get the boundary of a Simplex:
Get the boundary of a simplicial complex, represented as a list of simplices:
Get the boundary of a MeshRegion:
Scope (2)
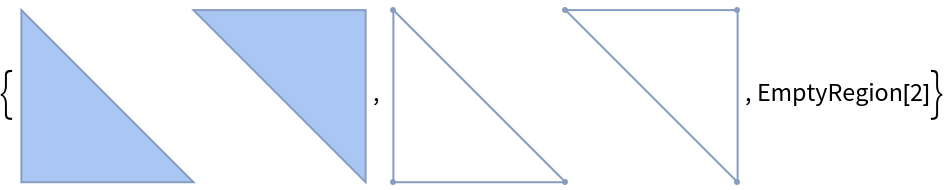
By default, the boundary will be computed from simplices that match the dimension of the simplicial complex:
A different dimension k can be specified, which will find the boundary of the k-skeleton of the complex:
Generalizations and Extensions (1)
Some other primitives can represent a simplex as well:
Applications (2)
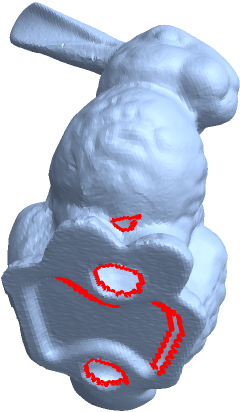
Find holes in a 3D model:
Highlight the boundary edges:
Properties and Relations (3)
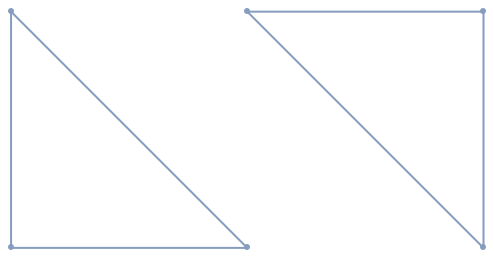
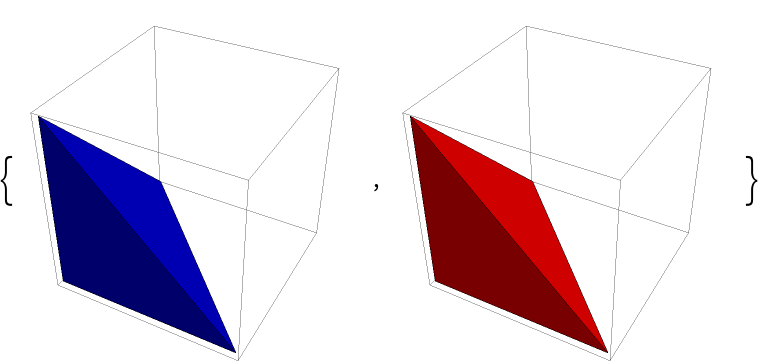
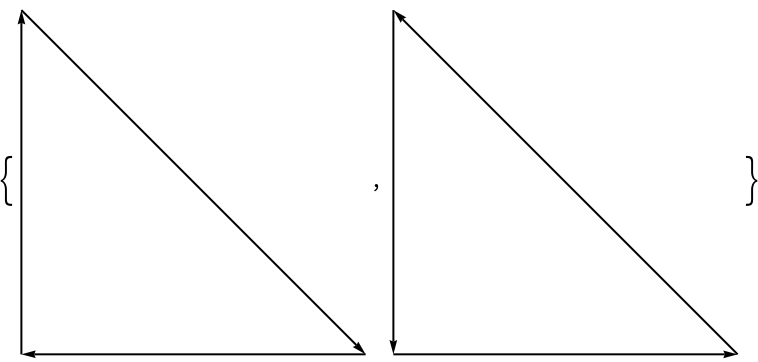
Orientation is preserved:
The boundary of a boundary is always empty:
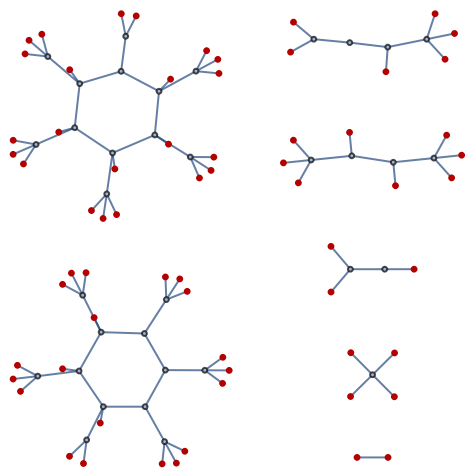
A graph can be considered a one-dimensional simplicial complex:
The boundary can give you information about degree of vertices:
Possible Issues (5)
Not all graphics primitives are valid simplices:
They can often be converted to simplicial complexes using DiscretizeGraphics that are reasonable approximations:
Valid n-dimensional simplices must have n+1 vertices:
Mesh regions are not necessarily composed of simplices:
TriangulateMesh can often be used to create a valid simplicial complex:
Vertices must be unique:
If orientations are not consistent within a simplicial complex, the boundary will not have consistent orientations, either:
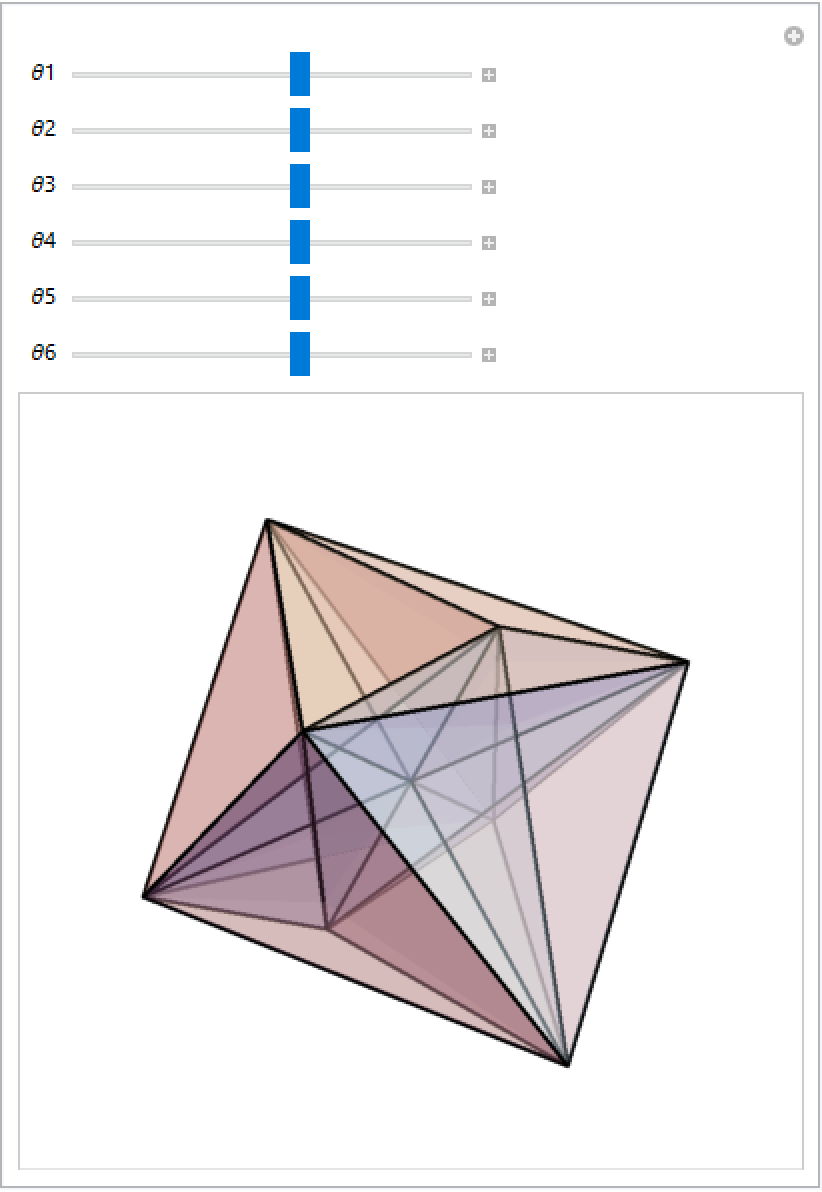
Interactive Examples (1)
One can visualize 4D shapes by rotating and projecting the boundary into 3D. Here is an example using a hexadecachoron:
Neat Examples (2)
The boundary of an annulus is two circles, while the boundary of a Moebius strip is a single circle:
Get text outlines:



![pts = {{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}};
boundary = ResourceFunction["SimplexBoundary"][Tetrahedron[{1, 2, 3, 4}]];
insideOutBoundary = ResourceFunction["SimplexBoundary"][Tetrahedron[{2, 1, 3, 4}]];
{Graphics3D[{FaceForm[Red, Blue], GraphicsComplex[pts, boundary]}], Graphics3D[{FaceForm[Red, Blue], GraphicsComplex[pts, insideOutBoundary]}]}](https://www.wolframcloud.com/obj/resourcesystem/images/276/2769056c-388b-4cca-bc31-a2c9625a11f0/4d2f2d6848d779e8.png)
![pts = {{0, 0}, {1, 0}, {0, 1}};
boundary = ResourceFunction["SimplexBoundary"][Triangle[{1, 2, 3}]];
insideOutBoundary = ResourceFunction["SimplexBoundary"][Triangle[{2, 1, 3}]];
{Graphics[GraphicsComplex[pts, Arrow @@@ boundary]], Graphics[GraphicsComplex[pts, Arrow @@@ insideOutBoundary]]}](https://www.wolframcloud.com/obj/resourcesystem/images/276/2769056c-388b-4cca-bc31-a2c9625a11f0/2089e71ba24daa51.png)
![NestList[ResourceFunction["SimplexBoundary"],
MeshRegion[{{0, 0}, {1, 0}, {0, 1}, {1, 1}, {2, 1}, {2, 0}}, Polygon[{{1, 2, 3}, {4, 5, 6}}]], 2]](https://www.wolframcloud.com/obj/resourcesystem/images/276/2769056c-388b-4cca-bc31-a2c9625a11f0/3a325ead565651cd.png)
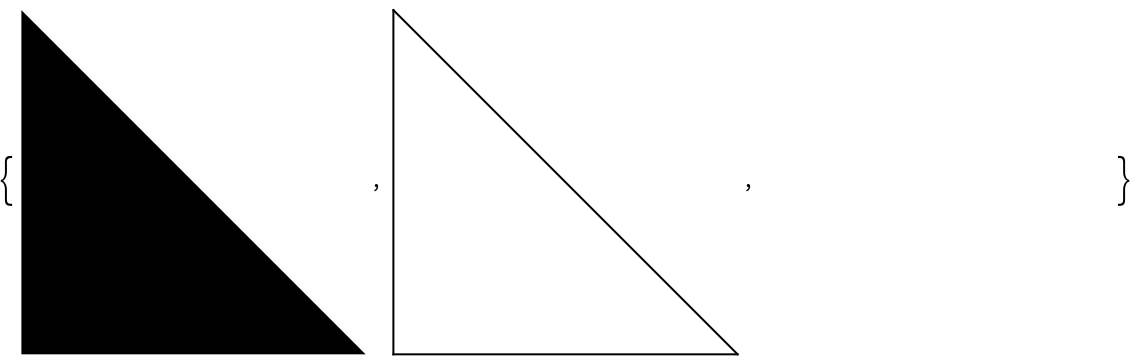
![Graphics /@ NestList[ResourceFunction[
"SimplexBoundary"], {Simplex[{{0, 0}, {1, 0}, {0, 1}}], Simplex[{{1, 1}, {1, 0}, {0, 1}}]}, 2]](https://www.wolframcloud.com/obj/resourcesystem/images/276/2769056c-388b-4cca-bc31-a2c9625a11f0/590b19ed221ad0ad.png)

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/7c3732eb-2f65-4916-9195-aa279a2784fc"]](https://www.wolframcloud.com/obj/resourcesystem/images/276/2769056c-388b-4cca-bc31-a2c9625a11f0/5ef6402870c27345.png)





![rotationFunction = Block[{\[Theta]1, \[Theta]2, \[Theta]3, \[Theta]4, \[Theta]5, \[Theta]6}, With[{rotateExpr = Simplify[
N[(Composition @@ RotationTransform @@@ Transpose[{{\[Theta]1, \[Theta]2, \[Theta]3, \[Theta]4, \[Theta]5, \[Theta]6}, Subsets[IdentityMatrix[4], {2}]}])[{x, y, z, w}]], Reals]},
Compile[{{r, _Real, 1}, {v, _Real, 1}},
Block[{\[Theta]1, \[Theta]2, \[Theta]3, \[Theta]4, \[Theta]5, \[Theta]6, x, y, z, w},
{\[Theta]1, \[Theta]2, \[Theta]3, \[Theta]4, \[Theta]5, \[Theta]6} = r;
{x, y, z, w} = v;
rotateExpr
],
CompilationOptions -> {"ExpressionOptimization" -> True},
RuntimeOptions -> "Speed",
RuntimeAttributes -> {Listable},
Parallelization -> True
]
]];
vertices = Flatten[Table[
Chop[rotationFunction[r, Prepend[IdentityMatrix[4], {0, 0, 0, 0}]]], {r, Pi*IdentityMatrix[6]}], 1];
hexadecachoron = Table[Simplex[{1, 2, 3, 4, 5} + 5 n], {n, 0, 5}]](https://www.wolframcloud.com/obj/resourcesystem/images/276/2769056c-388b-4cca-bc31-a2c9625a11f0/6bd7d4f1d6d3a780.png)
![Manipulate[
Graphics3D[{EdgeForm[Thick], Opacity[.25], GraphicsComplex[
rotationFunction[{\[Theta]1, \[Theta]2, \[Theta]3, \[Theta]4, \[Theta]5, \[Theta]6}, vertices][[All, ;; 3]], ResourceFunction["SimplexBoundary"][hexadecachoron]]}, PlotRange -> 1, ViewAngle -> Pi/10, Boxed -> False],
{{\[Theta]1, 1}, -2 Pi, 2 Pi},
{{\[Theta]2, 1}, -2 Pi, 2 Pi},
{{\[Theta]3, 1}, -2 Pi, 2 Pi},
{{\[Theta]4, 1}, -2 Pi, 2 Pi},
{{\[Theta]5, 1}, -2 Pi, 2 Pi},
{{\[Theta]6, 1}, -2 Pi, 2 Pi}
]](https://www.wolframcloud.com/obj/resourcesystem/images/276/2769056c-388b-4cca-bc31-a2c9625a11f0/33706cac79d37f92.png)
![{ResourceFunction["SimplexBoundary"][\!\(\*
GraphicsBox[
TagBox[
DynamicModuleBox[{
Typeset`mesh = {MeshRegion, {Method -> {"PropagateMarkers" -> False}}}},
TagBox[GraphicsComplexBox[CompressedData["
1:eJxVVH1M1HUYP0loWtZc+dJgAhnnelsM+qfJekJBDTVfpkbFQbUoXxCSlQ0J
KePo4MzE1dqIGLqFAVnKiyy6fFBepvHS8XLOBkRB56Lj/YB1cN2V9/08t/3Y
2Hf3/T3f5/l8Ps/necJfz9idGqDT6b78///O2bY+983SstvUqU5O+C3w3abF
I9QzZh4qcw5z/MvLXjKsdlBhR/jD+4P+oCNJbRWW3lG6WnVke2NzH6U88MbJ
nPYJei3jyejaCgsdGEkMLImaoBPxAcOns9vJXXHg54S1Ns4ngzXh6XH6QN2z
xG1FvS5Vj1KRR/LmIY/E3530YLS+vChG5/ub9OOKA85rwCU4u5FX6jSq7yzf
jT5cHgqovIPTzm/77t3U4otzcDt06YBO0IclL3ixzvfeRur9KDcBB3jxNtQH
D84HL/DkRMWbwYsVz7Mx0J8LFE/BzQweyMtW1JH8x6Gz6LTE2jIeZfrCYkYe
6MXNyCO404FDcC0tLN32TFalRXDNq376eV8Bz0y8L9D2l9/X9o+N8IHS28b7
0Vcz3gEH9O8TXiQ8xZfSB+mLnPnop8eH0w4fuOFXB/T2wq+Cywu/9gsvvLeR
4q17Tul33qLqzJGcygdO+MvlP7twr/q3AJ9OkVerH37b/bjzgENwXQNu4SF5
4pBX+WKKpQ7qwhcu+N3B8t6geLPooOaxn6We+E54p0IniTdo/UHiS9kTat7t
LHzEZ2bNnC7g9xTmxY15cWC+XCy6qvmbY9FbfHkQewJ1eAF1wQP+7xeeiG+X
fjYqnpdiJD5f038P5tnu9/kC9hh0xPw5/PkToavsUdkbncAvPHrQH+GZru0H
5sffD16EOcHcSJ9Z+o4+Y06coiuLzs3AKTrv0e5X5Lcjvwff/f3G/Pr9iH3Q
YBEdTeir7CkT+io4gYsE5xX0ORN45rX+543w0Un4aiN8fRK8oBuJjm3whegs
vszU+NSL3+3YN17sm34uf/bc2ufDnBxWv7n20Ufs/OpVT153cQ2XLLN+nt81
y7FLJzI+SRhhfcErpz7qnvLfJ6k4+vGgudywdZJXrdi0xxg6RhsWPxVyYUsH
Hzrc2rvFPEt2Z8jeyz/8TvpvNwxmR84w4ilExfPHzevf+d47Q72bvfG2qFv8
N+IjVDz9hHjJb0K8VcXTd03VyQM9U9zVuav0m4IB3nfsbGOoZ5zLbgQNGaod
7E4rdtftuETelMuta+KcvM5xPLmm7wavPDX26eogJ8c+NHh+SdUQ70qsiT0x
PMkSpzvse+ePi1DvKPfMryHHIqd50+DOoyuD/6R7M40rkupHuDf4Qtr11lE6
FFq3KMA6yCnG3OkXo50UiDzISxezjDv0yTYqiRz4padwmknVp92of4/KRzdV
PkY9SlD1eLi4tmqWZ6jwqGvVXV9Xc602H4EPgQ/NN0waT2dN0Gc5MV9F7L1N
92nzE/hROPhBT7qp9KT0nOVh6yr/4bCGEsf2tH7W45R7OR9T99Q6e+uJvtox
Tl4+ty9wYoZMOz9M/zeonkznshPLylyUnB1eVBfVRXMFa94KfcHFLSqeUlQ8
X3xcX3P/e3MUXOQo8fb+Rdfx3YB8/wEFNBJf
"],
{Hue[0.6, 0.3, 0.95], EdgeForm[Hue[0.6, 0.3, 0.75]],
TagBox[PolygonBox[CompressedData["
1:eJwNw4V2qgAAANBNF67LpesO152uu7vDdTrEQgURKQUsQOp/3ne93XNuk9V2
aNWlpaX9+6v/W3sEm2ph5Obs7BxEzkAwaIZ54JjfGRvxwUf18wsuEwzcIEAN
Vg3wx7v8yYNwdyFcXtgFNND8+C6HtqvQ9quSX8gqPwWbGu/pDsQE1JmQG+B6
b98RQO3H18ApYkab2xvNwTrktLAgSpRVCnZ0HXeKe44Tx34y4WchG7YdWs6n
KtbwrU3n9KS3qjy0jdUc7IkH4iEuhnrjRbkcNZTMcG6ux33aljO1voHHkurc
Vioa17CQwzslyQH7VRA1lhG40VmcTZ7fgk4j8en5wuqryRRhRkCicoVctaRm
51h/oiGRaVimvr880rxr1bUgbhySBheZbUj61VXStWbE+/rVaFF8d4cP3Lc0
B1rc8ntnN0PfB+i2Vrq1w/ooK5FwJwPR4ba28DNeXlGPwZH0np5wRMd8eBgd
l5vX8xyW6YDy+l2Oh16Vl4guvQQqZUohzRv9LGWY7g/G89kJdUFsV/CqiR3w
96n+hh+W/elSfTHbMGuDfpcWpWltxqN8k8TKxZMdvBO8k1NcYVQfy0lZZntj
cccJz0W9I6Oa8vZSFC3g8ibe39yL81J+LjVRyElTSw4ec1ESGhQol2Gwzw9j
fFKf4dFFwrSbXClOZGXGY76BQT87PPAk27MSQ4on0sAmlLB7XO0f0XzatHdD
xEOiwytx6pjPkiK10RmKk3JivWPqOJFyym46OZR4uBRAIfimuO/AW30y9h+L
MeVS
"]],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics",
AutoDelete->True,
Editable->False,
Selectable->False],
DefaultBaseStyle->{"MeshGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
ImageSize->{Automatic, 99.8576}]\)], ResourceFunction["SimplexBoundary"][\!\(\*
Graphics3DBox[
TagBox[
DynamicModuleBox[{Typeset`mesh = {MeshRegion, {}}},
TagBox[GraphicsComplex3DBox[CompressedData["
1:eJx1WGlsFVUYnbavLYjs+gOS6qAGg2iIQDEp4b0RsBBCWBMFpHYgUgRR5Aea
aDQTEAJCoYUgAakOCSkmQGRTK0LnIkiISCwgWFnK0EKBlqWlWLALz7lnZsK5
E3lJM7lnvvnuty/tM3P+pFmpmqad9P7SNP83oK2T4T2Mgz/uT3hPsWmOJZ9G
1q2uEjfzCyrk2ew2x8bTbMqUuJa/8WhCe/izkkcyJK73Nm4xbv9R00XiYsqg
BvB/7S0hn/aYpZ1Bn3ntHujdj8DP3DaoGfePHJVuMP/OXTR5tpo/eUw+7drZ
FyWd9fm5+/iutOfjkDdt4SWcC7/B91bRqbssj/nxVuhrvtQ3ie+rhkI/d1Ju
Kujfz0oyvbt6YkfIMfEK3hs/vfCnfK8PLIa+xtWzvpx5sUroV/IM5BQjD6ew
/NqLC9PA/+WCDvLp7j98DvfsWQV7unVTq/lerbgM9nf16S741hbsxL39P2yF
3M9+l8b8jcq1sK/RtCSDcXP4uEbYY9HzsLfxw7M1OC+42e5IPmsOpSp8eu5O
StzsXgY+IiX/BuibxqcK+f5uvxj0ODv8Juz2VUmZpHf/astU7v1sUTn8POJn
38/pI2pxnlt8RtKLrDhwc8rOq5B7+/Qr0P+fWQofuyob8tq79oLezS2/DP2H
ZEEOsWxAC9tN/3ZLleRvx3ep8uQcv457K4cjTgwRuw57plbfl7iRXBJjev1Y
xxbQL78Lf4kJefWgL5xQL3G9S6rC3+p/oAl2WHEC8WmdidfBbi3vAbf73lHi
WWuJZ0h7uqPS7jgEu8/lZEpcz8hvBr/1A2/jfXY7cPvJ8zjrLV/i6S4fliJx
LXe3xvyNWjMGfMhUPw7rM5GX7ozrwN3bhfeUPF2bDnnE+G1t8MfbO3x6kicR
yJOIyK/ELcmZCOQEv66v+HjF1GtMb+wb30Hi1ugGxL/e56xP/1tRusSNrC03
HOKjN8cgv9F7dFNon6hebE/778GIW+3gHuChXmLVccijvVtYqdBX7QJudn/j
KPLgSKvPf9tx6GuvOHTJYTlJL+bD/JX4rB4MfY3SC369C/ibZfNPgm5TjRr/
1UPTwGfd922KnE5/DXw+WNYKPPAvx6dgeTqdrkO+T8uBPcL4tJ++4cIu3Zf7
+R3kBdcH5uMW1eE+0e/AA7wP6oAYkQP7mtmlkCusG5xfzMdamYe4Nx9sQPyG
+cX6KnWY4pz5cL4r+vbY9Dvs0NvXK6wzXK8UebaX7YY/58VBH9Yrzl+m934d
Imf82I+K3VZfOAM7HdsBPcI6xnVboV8bw3tt43nfz0HdNi5qvl3HbfbrdNDv
7GtbUeeNbno7zl5/hP5fNKD/iauvok7KvgP9qd9xXFm/nPLrwpiefh4Ffc2Y
OxbfW8ts2CPsg9xnmY+x5nX4Ty+oR50K+6w96TbkEz2G+fkS9H2eHxR5Sp5A
PzYaxyJOw/mB67+Sd9R/2Z5sB0d72H+5nzI929PRHs4b3K/5Xr3Xr/48sX5m
BeQM+rWb2+jLn5wt4K//maMeZbdEYDcnYrdEYDcn4pdE4BfgFCe4z4sTJ+Lf
ROBfJ2LnRGBnJ6JXItDLieiVCPQCTnEr9ZNxC5ziH/bz4h9yUp0P+wXupToP
OwZ9kPNa8pF5DfkpfyUu8xd2ozoJubw6CXmojkE/r46Bnuoh5PfqIeioviG+
vPqGe6mOAffqGOip3kpc1lvwpTmH443nXsa578A+Xt+BnNTX8J3X14BT/4Jf
vP6Ce6nPOsSH+5FD9MJq9+fLTxfvxTnYCyxNQ96ZeYvXlcvzpewZcV9Uf046
XbGhnOTnucIhOXmeFGR/nlsE+YvnMUF25nlVkF947sU9QRzyPCnxMA55fhPk
L55XYdcg3nieFBQnPPdKPIxD3lPAJ8hHnvPDuoF7aW8K6x7sQHsH7BPkL+8X
0Cuo87w3IY6CvsB7DeQP6gbvZWF9hl60N4X1HO9pfwzjBH6h/TGse3jvzUUS
t+epc5Gco0B/Qp0PhTfXgX+DOq9a3pwAPDon/Bv37TNanUtFSrVv/8icL7y5
AvpG5mfdm3/gx8h+xHmRIH11b07AOTLnmysnYK4xIvuCua6kDHUtsjdpk3P9
+SOyh1qlW6rAP7LXaDumX4EfInuTtm/+SeDRedKbNyBvZE8UXv0BHt27vf4I
/0X2Tdfrs1JOO7Ln2l5flrgZ3cu8vilxLdI3LW9+gL7RPd3rjxJ331T/z2B7
cwL491L/z8D8H8WH72U+j5JHoSe9GGd/KXzIX4JxsifjbH/G2c6Msx8ZZ78z
zvGm4BSfCh+KK8Y5zhX5KU/ZDpx3ih0ofxV6ykflXspHxjnfFT5UZxjnOqP4
K5lEHdPHPfW17GdhXzMmtyEP3Wlzdgb5XuRE8KDuFSHuUjTUEfdydnHAZ4Hs
h/rSVtRDu/EdkWD6ZBK4UZO9OaSPR+hD/s5/DtcfFw==
"],
{Hue[0.6, 0.3, 0.85], EdgeForm[Hue[0.6, 0.3, 0.75]],
TagBox[Polygon3DBox[CompressedData["
1:eJwBvwNA/CFib1JiAgAAADoBAAADAAAAAQIDBAUGBwgJCgYLDA0ODw4QERIF
ExAIFAkVFhcYGRobHBUdHgsNHxsgISIXIyAkJSQiJicoKRgqKywtLi0vMC8x
JjIzNDM1Njc4OTgyOjE7PB0aPTU+P0BBQkNERURGRyosSD5DSUFKS0pMTUZA
Tjs3T0xQUVJTE1RVVldYWVpbXFtdXlhaX2BXYWJgY11kZWZkCmdoHmlnB2pU
DGtpEWxtbgNtD1VrFG9qHHBvLnFyGXN0KXV2PHRwH3dzIXh5I3p3JXl6e1BS
FnZ4fFNiMH1xK3J+R351On99OSiAToF/NoCBgoOENIUnSIaHRYiJe4qLTYyI
SY2OS4+NQomGT4uPUZCKY5GSX5OUfJWQP46MVpaTXJKXXpiWWZeYPYeFmZpm
mwMSmxFtnBEFnR5nnh4NnwponQoLnARsYZSVngxpoBMIoQ9rog8Qo4QDoQwO
oAdUpAcJohNVpBRqpRQVpRxvpjwapykqqDxwphl0qR8gqhkbqh9zp0d1qSN3
qyV6rCF5rSEXqyMkrRZ4ril2rCUirhYYBGhsr0cssDY4sS5ysk5/sSstsy4v
tDp9szBxtDAxryt+sjo7qBwdsDmAtTaBtU43tjkytzQntiYotyYzuDQ1uD2F
uT0+unuLu0JEvEVGvE2Iu0WJvUKGvUhDvk1Avj+Mv0uNwEtMwXtSwE+PwkmO
wj9Buk9QwVGKw1FTxFmYxXxixlZYw3yQxWGVx19XyGFgyF+Uv0lKx1aTgoRm
yVlbxF5axl6WyVyXymNky1xdy2OSymaRzAGEFq52EZsSE6BUA5ttzaNuBJ9o
EZxsBJwFB6AICp8GHp0LDJ4NDKFrCp1nD6EOE6IQHp5pD6JVKa4YB6RqI6t6
HKUVH6obFKVvHKhwGaYaPKgdPKZ0FKQJGapzAwISJaskI6kgH6l3Jax5Fq0X
IawiIa14nwQGKad1XsSYOrQxK7FyLrNxMLMvLrEtK68sR69+MLR9OrJ/TrI7
NrCAuUiHObYoObA4JrcnJrYyNLczPbg1P8KOSLk+TbxGPbmHSL2GRbtEQr1D
QruJNrU3RbyINLiFScJBP75ATb6MSb+NT8BMS79KS8CPTrWBT7qLe7pQY8td
fMWVfMNTYciUYcViY8qRX8hgZspkUcOQVsdXWcRaWcmXX8eTXMlbXsZYVsaW
XMuSR6cqzoJlo83Pg4LPg6PPZpqR0AHRbqMDe8GKhAEDAczRzJmE0pnRhJlm
gs7PZYJmo4OEmczRUcFSAdACmdKaydpvxw==
"]],
Annotation[#, "Geometry"]& ]}],
MouseAppearanceTag["LinkHand"]],
AllowKernelInitialization->False],
"MeshGraphics3D",
AutoDelete->True,
Editable->False,
Selectable->False],
Boxed->False,
DefaultBaseStyle->{"MeshGraphics3D", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]},
ImageSize->{Automatic, 101.06325221053599`},
Lighting->{{"Ambient",
GrayLevel[0.45]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{2, 0, 2}]}, {"Directional",
GrayLevel[0.33],
ImageScaled[{2, 2, 2}]}, {"Directional",
GrayLevel[0.3],
ImageScaled[{0, 2, 2}]}},
Method->{"ShrinkWrap" -> True},
ViewPoint->{1.3, -2.4, 2.},
ViewVertical->{0., 0., 1.}]\)]}](https://www.wolframcloud.com/obj/resourcesystem/images/276/2769056c-388b-4cca-bc31-a2c9625a11f0/17ec641559e518c0.png)

